Stability properties of gradient flow dynamics for the symmetric low-rank matrix factorization problem

The symmetric low-rank matrix factorization serves as a building block in many learning tasks, including matrix recovery and training of neural networks. However, despite a flurry of recent research, the dynamics of its training via non-convex factorized gradient-descent-type methods is not fully understood especially in the over-parameterized regime where the fitted rank is higher than the true rank of the target matrix. To overcome this challenge, we characterize equilibrium points of the gradient flow dynamics and examine their local and global stability properties. To facilitate a precise global analysis, we introduce a nonlinear change of variables that brings the dynamics into a cascade connection of three subsystems whose structure is simpler than the structure of the original system. We demonstrate that the Schur complement to a principal eigenspace of the target matrix is governed by an autonomous system that is decoupled from the rest of the dynamics. In the over-parameterized regime, we show that this Schur complement vanishes at an $O(1/t)$ rate, thereby capturing the slow dynamics that arises from excess parameters. We utilize a Lyapunov-based approach to establish exponential convergence of the other two subsystems. By decoupling the fast and slow parts of the dynamics, we offer new insight into the shape of the trajectories associated with local search algorithms and provide a complete characterization of the equilibrium points and their global stability properties. Such an analysis via nonlinear control techniques may prove useful in several related over-parameterized problems.

From exponential to finite/fixed-time stability: Applications to optimization

The development of finite/fixed-time stable optimization algorithms typically involves study of specific problem instances. The lack of a unified framework hinders understanding of more sophisticated algorithms, e.g., primal-dual gradient flow dynamics. The purpose of this paper is to address the following question: Given an exponentially stable optimization algorithm, can it be modified to obtain a finite/fixed-time stable algorithm? We provide an affirmative answer, demonstrate how the solution can be computed on a finite-time interval via a simple scaling of the right-hand-side of the original dynamics, and certify the desired properties of the modified algorithm using the Lyapunov function that proves exponential stability of the original system. Finally, we examine nonsmooth composite optimization problems and smooth problems with linear constraints to demonstrate the merits of our approach.

Stability of Primal-Dual Gradient Flow Dynamics for Multi-Block Convex Optimization Problems

We examine stability properties of primal-dual gradient flow dynamics for composite convex optimization problems with multiple, possibly nonsmooth, terms in the objective function under the generalized consensus constraint. The proposed dynamics are based on the proximal augmented Lagrangian and they provide a viable alternative to ADMM which faces significant challenges from both analysis and implementation viewpoints in large-scale multi-block scenarios. In contrast to customized algorithms with individualized convergence guarantees, we provide a systematic approach for solving a broad class of challenging composite optimization problems. We leverage various structural properties to establish global (exponential) convergence guarantees for the proposed dynamics. Our assumptions are much weaker than those required to prove (exponential) stability of various primal-dual dynamics as well as (linear) convergence of discrete-time methods, e.g., standard two-block and multi-block ADMM and EXTRA algorithms. Finally, we show necessity of some of our structural assumptions for exponential stability and provide computational experiments to demonstrate the convenience of the proposed dynamics for parallel and distributed computing applications.

Accelerated forward-backward and Douglas-Rachford splitting dynamics

We examine convergence properties of continuous-time variants of accelerated Forward-Backward (FB) and Douglas-Rachford (DR) splitting algorithms for nonsmooth composite optimization problems. When the objective function is given by the sum of a quadratic and a nonsmooth term, we establish accelerated sublinear and exponential convergence rates for convex and strongly convex problems, respectively. Moreover, for FB splitting dynamics, we demonstrate that accelerated exponential convergence rate carries over to general strongly convex problems. In our Lyapunov-based analysis we exploit the variable-metric gradient interpretations of FB and DR splittings to obtain smooth Lyapunov functions that allow us to establish accelerated convergence rates. We provide computational experiments to demonstrate the merits and the effectiveness of our analysis.

Provably Efficient Generalized Lagrangian Policy Optimization for Safe Multi-Agent Reinforcement Learning

We examine online safe multi-agent reinforcement learning using constrained Markov games in which agents compete by maximizing their expected total rewards under a constraint on expected total utilities. Our focus is confined to an episodic two-player zero-sum constrained Markov game with independent transition functions that are unknown to agents, adversarial reward functions, and stochastic utility functions. For such a Markov game, we employ an approach based on the occupancy measure to formulate it as an online constrained saddle-point problem with an explicit constraint. We extend the Lagrange multiplier method in constrained optimization to handle the constraint by creating a generalized Lagrangian with minimax decision primal variables and a dual variable. Next, we develop an upper confidence reinforcement learning algorithm to solve this Lagrangian problem while balancing exploration and exploitation. Our algorithm updates the minimax decision primal variables via online mirror descent and the dual variable via projected gradient step and we prove that it enjoys sublinear rate $ O((|X|+|Y|) L \sqrt{T(|A|+|B|)}))$ for both regret and constraint violation after playing $T$ episodes of the game. Here, $L$ is the horizon of each episode, $(|X|,|A|)$ and $(|Y|,|B|)$ are the state/action space sizes of the min-player and the max-player, respectively. To the best of our knowledge, we provide the first provably efficient online safe reinforcement learning algorithm in constrained Markov games.

Tradeoffs between convergence rate and noise amplification for momentum-based accelerated optimization algorithms

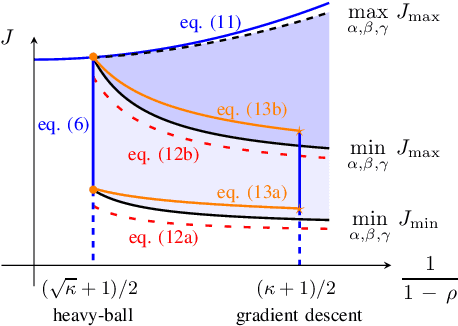
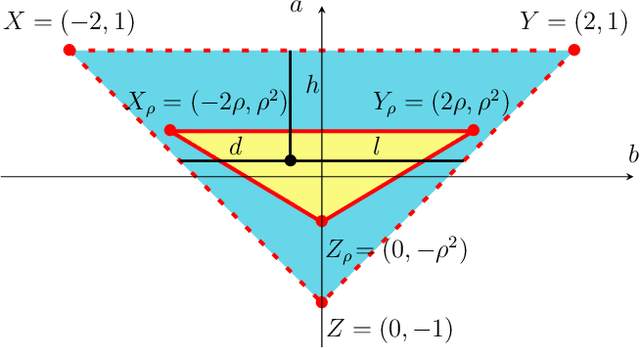
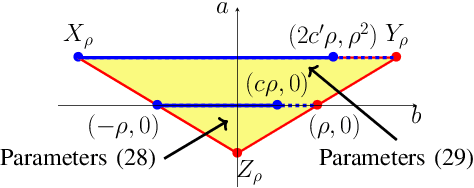
We study momentum-based first-order optimization algorithms in which the iterations utilize information from the two previous steps and are subject to an additive white noise. This class of algorithms includes heavy-ball and Nesterov's accelerated methods as special cases. For strongly convex quadratic problems, we use the steady-state variance of the error in the optimization variable to quantify noise amplification and exploit a novel geometric viewpoint to establish analytical lower bounds on the product between the settling time and the smallest/largest achievable noise amplification. For all stabilizing parameters, these bounds scale quadratically with the condition number. We also use the geometric insight developed in the paper to introduce two parameterized families of algorithms that strike a balance between noise amplification and settling time while preserving order-wise Pareto optimality. Finally, for a class of continuous-time gradient flow dynamics, whose suitable discretization yields two-step momentum algorithm, we establish analogous lower bounds that also scale quadratically with the condition number.

Convergence and sample complexity of natural policy gradient primal-dual methods for constrained MDPs

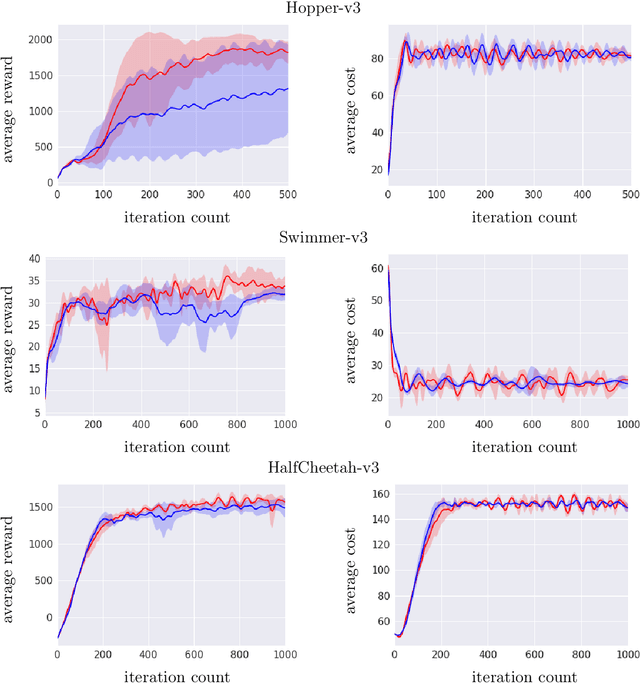
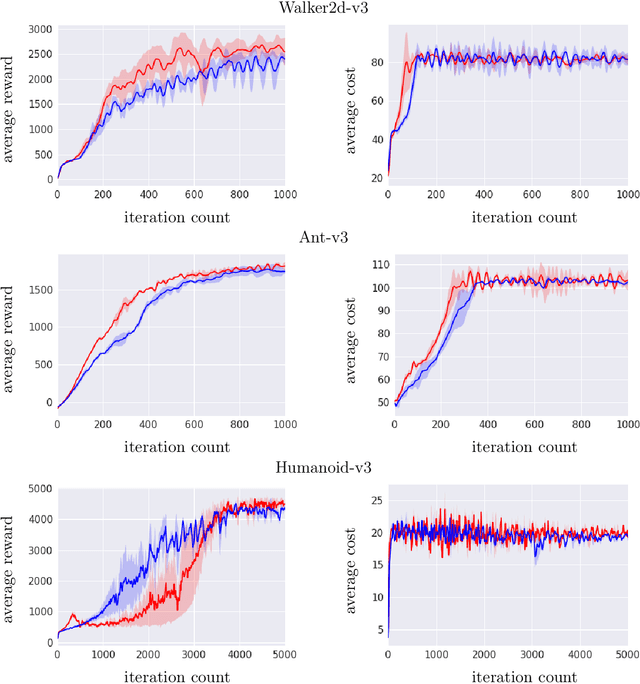
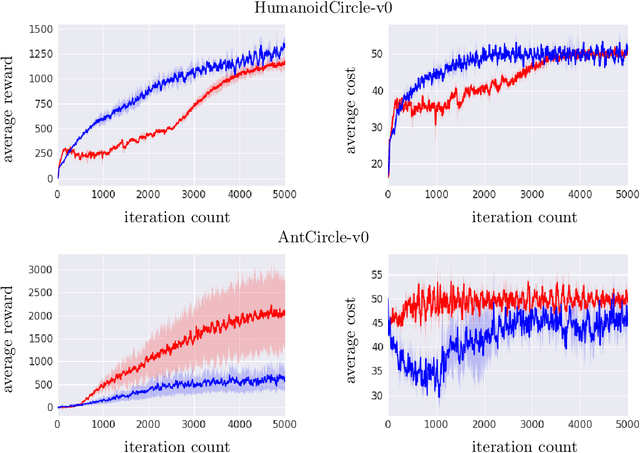
We study sequential decision making problems aimed at maximizing the expected total reward while satisfying a constraint on the expected total utility. We employ the natural policy gradient method to solve the discounted infinite-horizon optimal control problem for Constrained Markov Decision Processes (constrained MDPs). Specifically, we propose a new Natural Policy Gradient Primal-Dual (NPG-PD) method that updates the primal variable via natural policy gradient ascent and the dual variable via projected sub-gradient descent. Although the underlying maximization involves a nonconcave objective function and a nonconvex constraint set, under the softmax policy parametrization we prove that our method achieves global convergence with sublinear rates regarding both the optimality gap and the constraint violation. Such convergence is independent of the size of the state-action space, i.e., it is~dimension-free. Furthermore, for log-linear and general smooth policy parametrizations, we establish sublinear convergence rates up to a function approximation error caused by restricted policy parametrization. We also provide convergence and finite-sample complexity guarantees for two sample-based NPG-PD algorithms. Finally, we use computational experiments to showcase the merits and the effectiveness of our approach.

Independent Policy Gradient for Large-Scale Markov Potential Games: Sharper Rates, Function Approximation, and Game-Agnostic Convergence

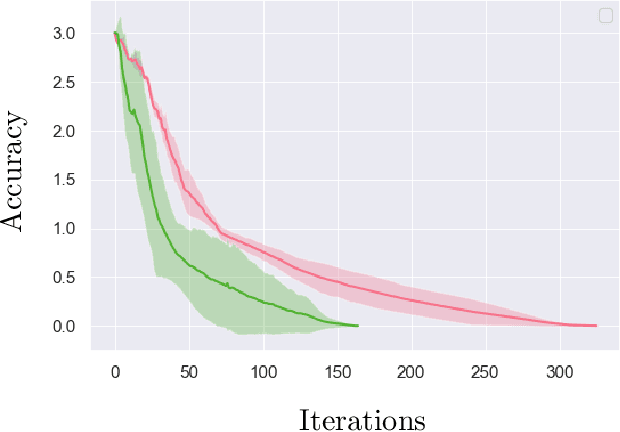
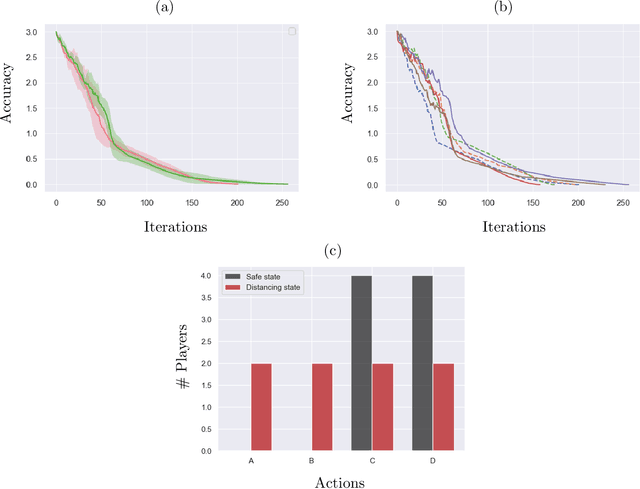
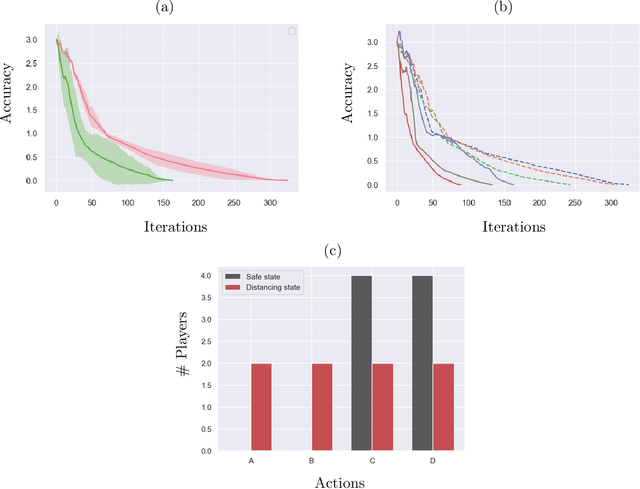
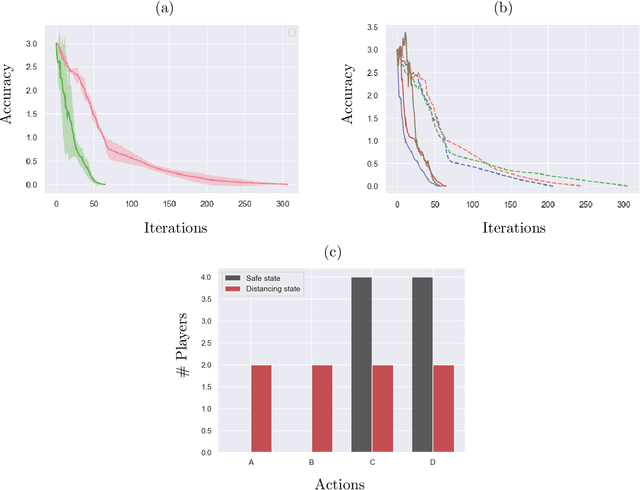
We examine global non-asymptotic convergence properties of policy gradient methods for multi-agent reinforcement learning (RL) problems in Markov potential games (MPG). To learn a Nash equilibrium of an MPG in which the size of state space and/or the number of players can be very large, we propose new independent policy gradient algorithms that are run by all players in tandem. When there is no uncertainty in the gradient evaluation, we show that our algorithm finds an $\epsilon$-Nash equilibrium with $O(1/\epsilon^2)$ iteration complexity which does not explicitly depend on the state space size. When the exact gradient is not available, we establish $O(1/\epsilon^5)$ sample complexity bound in a potentially infinitely large state space for a sample-based algorithm that utilizes function approximation. Moreover, we identify a class of independent policy gradient algorithms that enjoys convergence for both zero-sum Markov games and Markov cooperative games with the players that are oblivious to the types of games being played. Finally, we provide computational experiments to corroborate the merits and the effectiveness of our theoretical developments.

Transient growth of accelerated first-order methods for strongly convex optimization problems

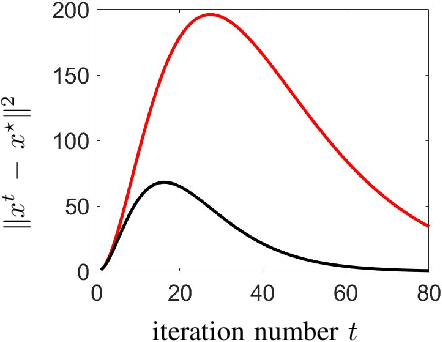
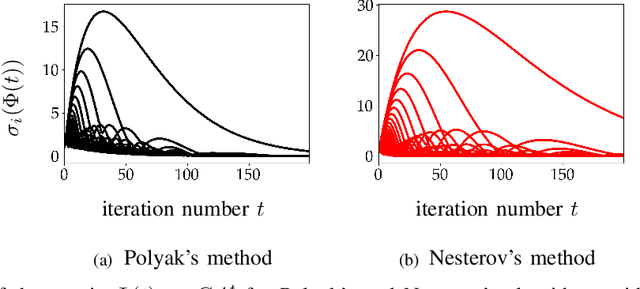
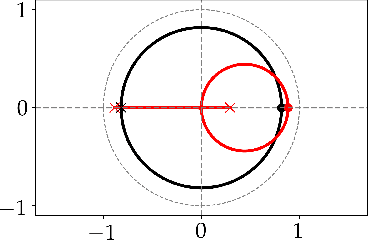
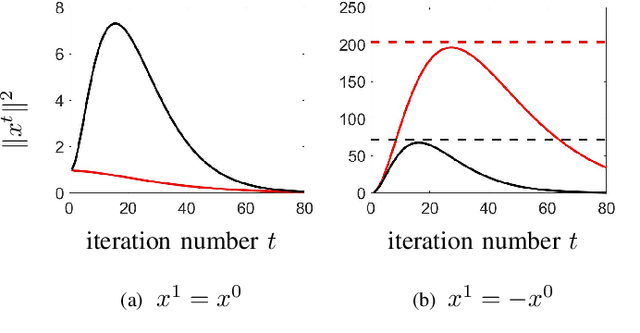
Optimization algorithms are increasingly being used in applications with limited time budgets. In many real-time and embedded scenarios, only a few iterations can be performed and traditional convergence metrics cannot be used to evaluate performance in these non-asymptotic regimes. In this paper, we examine the transient behavior of accelerated first-order optimization algorithms. For quadratic optimization problems, we employ tools from linear systems theory to show that transient growth arises from the presence of non-normal dynamics. We identify the existence of modes that yield an algebraic growth in early iterations and quantify the transient excursion from the optimal solution caused by these modes. For strongly convex smooth optimization problems, we utilize the theory of integral quadratic constraints to establish an upper bound on the magnitude of the transient response of Nesterov's accelerated method. We show that both the Euclidean distance between the optimization variable and the global minimizer and the rise time to the transient peak are proportional to the square root of the condition number of the problem. Finally, for problems with large condition numbers, we demonstrate tightness of the bounds that we derive up to constant factors.

Provably Efficient Safe Exploration via Primal-Dual Policy Optimization

We study the Safe Reinforcement Learning (SRL) problem using the Constrained Markov Decision Process (CMDP) formulation in which an agent aims to maximize the expected total reward subject to a safety constraint on the expected total value of a criterion function (e.g., utility). We focus on an episodic setting with the function approximation where the reward and criterion functions and the Markov transition kernels all have a linear structure but do not impose any additional assumptions on the sampling model. Designing SRL algorithms with provable computational and statistical efficiency is particularly challenging under this setting because of the need to incorporate both the safety constraint and the function approximation into the fundamental exploitation/exploration tradeoff. To this end, we present an {O}ptimistic {P}rimal-{D}ual Proximal Policy {OP}timization (OPDOP) algorithm where the value function is estimated by combining the least-squares policy evaluation and an additional bonus term for safe exploration. We prove that the proposed algorithm achieves an O(d^{1.5}H^{3.5}\sqrt{T}) regret and an O(d^{1.5}H^{3.5}\sqrt{T}) constraint violation, where d is the dimension of the feature mapping, H is the horizon of each episode, and T is the total number of steps. We establish these bounds under the following two settings: (i) Both the reward and criterion functions can change adversarially but are revealed entirely after each episode. (ii) The reward/criterion functions are fixed but the feedback after each episode is bandit. Our bounds depend on the capacity of the state space only through the dimension of the feature mapping and thus our results hold even when the number of states goes to infinity. To the best of our knowledge, we provide the first provably efficient policy optimization algorithm for CMDPs with safe exploration.