Transient growth of accelerated first-order methods for strongly convex optimization problems
Paper and Code
Mar 14, 2021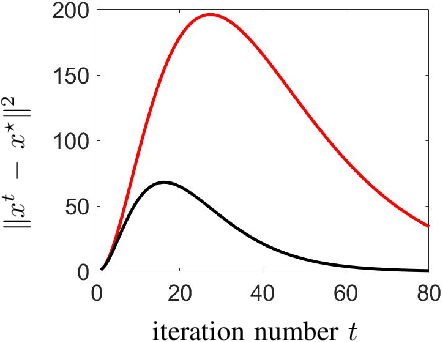
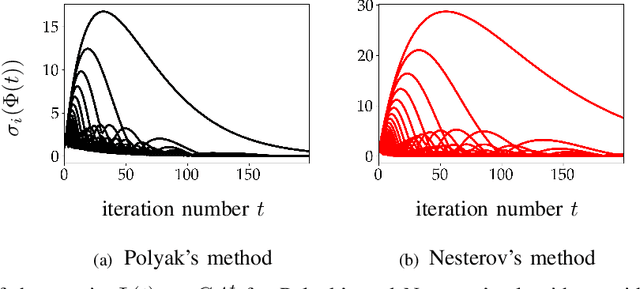
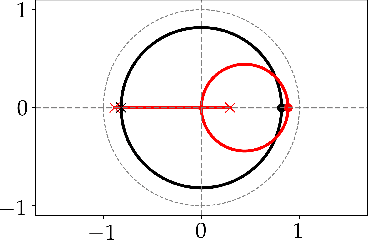
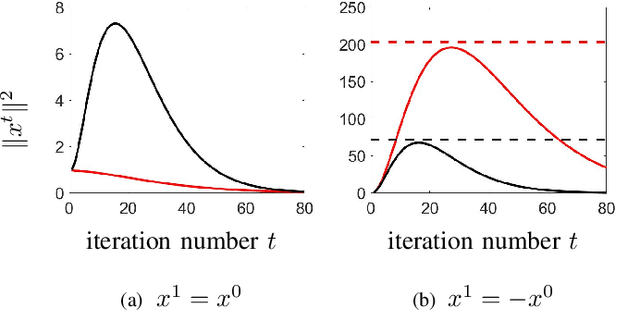
Optimization algorithms are increasingly being used in applications with limited time budgets. In many real-time and embedded scenarios, only a few iterations can be performed and traditional convergence metrics cannot be used to evaluate performance in these non-asymptotic regimes. In this paper, we examine the transient behavior of accelerated first-order optimization algorithms. For quadratic optimization problems, we employ tools from linear systems theory to show that transient growth arises from the presence of non-normal dynamics. We identify the existence of modes that yield an algebraic growth in early iterations and quantify the transient excursion from the optimal solution caused by these modes. For strongly convex smooth optimization problems, we utilize the theory of integral quadratic constraints to establish an upper bound on the magnitude of the transient response of Nesterov's accelerated method. We show that both the Euclidean distance between the optimization variable and the global minimizer and the rise time to the transient peak are proportional to the square root of the condition number of the problem. Finally, for problems with large condition numbers, we demonstrate tightness of the bounds that we derive up to constant factors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge