Decision Making in Hybrid Environments: A Model Aggregation Approach

Recent work by Foster et al. (2021, 2022, 2023) and Xu and Zeevi (2023) developed the framework of decision estimation coefficient (DEC) that characterizes the complexity of general online decision making problems and provides a general algorithm design principle. These works, however, either focus on the pure stochastic regime where the world remains fixed over time, or the pure adversarial regime where the world arbitrarily changes over time. For the hybrid regime where the dynamics of the world is fixed while the reward arbitrarily changes, they only give pessimistic bounds on the decision complexity. In this work, we propose a general extension of DEC that more precisely characterizes this case. Besides applications in special cases, our framework leads to a flexible algorithm design where the learner learns over subsets of the hypothesis set, trading estimation complexity with decision complexity, which could be of independent interest. Our work covers model-based learning and model-free learning in the hybrid regime, with a newly proposed extension of the bilinear classes (Du et al., 2021) to the adversarial-reward case. We also recover some existing model-free learning results in the pure stochastic regime.

Beating Adversarial Low-Rank MDPs with Unknown Transition and Bandit Feedback

We consider regret minimization in low-rank MDPs with fixed transition and adversarial losses. Previous work has investigated this problem under either full-information loss feedback with unknown transitions (Zhao et al., 2024), or bandit loss feedback with known transition (Foster et al., 2022). First, we improve the $poly(d, A, H)T^{5/6}$ regret bound of Zhao et al. (2024) to $poly(d, A, H)T^{2/3}$ for the full-information unknown transition setting, where d is the rank of the transitions, A is the number of actions, H is the horizon length, and T is the number of episodes. Next, we initiate the study on the setting with bandit loss feedback and unknown transitions. Assuming that the loss has a linear structure, we propose both model based and model free algorithms achieving $poly(d, A, H)T^{2/3}$ regret, though they are computationally inefficient. We also propose oracle-efficient model-free algorithms with $poly(d, A, H)T^{4/5}$ regret. We show that the linear structure is necessary for the bandit case without structure on the reward function, the regret has to scale polynomially with the number of states. This is contrary to the full-information case (Zhao et al., 2024), where the regret can be independent of the number of states even for unstructured reward function.

How Does Variance Shape the Regret in Contextual Bandits?

We consider realizable contextual bandits with general function approximation, investigating how small reward variance can lead to better-than-minimax regret bounds. Unlike in minimax bounds, we show that the eluder dimension $d_\text{elu}$$-$a complexity measure of the function class$-$plays a crucial role in variance-dependent bounds. We consider two types of adversary: (1) Weak adversary: The adversary sets the reward variance before observing the learner's action. In this setting, we prove that a regret of $\Omega(\sqrt{\min\{A,d_\text{elu}\}\Lambda}+d_\text{elu})$ is unavoidable when $d_{\text{elu}}\leq\sqrt{AT}$, where $A$ is the number of actions, $T$ is the total number of rounds, and $\Lambda$ is the total variance over $T$ rounds. For the $A\leq d_\text{elu}$ regime, we derive a nearly matching upper bound $\tilde{O}(\sqrt{A\Lambda}+d_\text{elu})$ for the special case where the variance is revealed at the beginning of each round. (2) Strong adversary: The adversary sets the reward variance after observing the learner's action. We show that a regret of $\Omega(\sqrt{d_\text{elu}\Lambda}+d_\text{elu})$ is unavoidable when $\sqrt{d_\text{elu}\Lambda}+d_\text{elu}\leq\sqrt{AT}$. In this setting, we provide an upper bound of order $\tilde{O}(d_\text{elu}\sqrt{\Lambda}+d_\text{elu})$. Furthermore, we examine the setting where the function class additionally provides distributional information of the reward, as studied by Wang et al. (2024). We demonstrate that the regret bound $\tilde{O}(\sqrt{d_\text{elu}\Lambda}+d_\text{elu})$ established in their work is unimprovable when $\sqrt{d_{\text{elu}}\Lambda}+d_\text{elu}\leq\sqrt{AT}$. However, with a slightly different definition of the total variance and with the assumption that the reward follows a Gaussian distribution, one can achieve a regret of $\tilde{O}(\sqrt{A\Lambda}+d_\text{elu})$.

Corruption-Robust Linear Bandits: Minimax Optimality and Gap-Dependent Misspecification

In linear bandits, how can a learner effectively learn when facing corrupted rewards? While significant work has explored this question, a holistic understanding across different adversarial models and corruption measures is lacking, as is a full characterization of the minimax regret bounds. In this work, we compare two types of corruptions commonly considered: strong corruption, where the corruption level depends on the action chosen by the learner, and weak corruption, where the corruption level does not depend on the action chosen by the learner. We provide a unified framework to analyze these corruptions. For stochastic linear bandits, we fully characterize the gap between the minimax regret under strong and weak corruptions. We also initiate the study of corrupted adversarial linear bandits, obtaining upper and lower bounds with matching dependencies on the corruption level. Next, we reveal a connection between corruption-robust learning and learning with gap-dependent mis-specification, a setting first studied by Liu et al. (2023a), where the misspecification level of an action or policy is proportional to its suboptimality. We present a general reduction that enables any corruption-robust algorithm to handle gap-dependent misspecification. This allows us to recover the results of Liu et al. (2023a) in a black-box manner and significantly generalize them to settings like linear MDPs, yielding the first results for gap-dependent misspecification in reinforcement learning. However, this general reduction does not attain the optimal rate for gap-dependent misspecification. Motivated by this, we develop a specialized algorithm that achieves optimal bounds for gap-dependent misspecification in linear bandits, thus answering an open question posed by Liu et al. (2023a).

Offline Reinforcement Learning: Role of State Aggregation and Trajectory Data

We revisit the problem of offline reinforcement learning with value function realizability but without Bellman completeness. Previous work by Xie and Jiang (2021) and Foster et al. (2022) left open the question whether a bounded concentrability coefficient along with trajectory-based offline data admits a polynomial sample complexity. In this work, we provide a negative answer to this question for the task of offline policy evaluation. In addition to addressing this question, we provide a rather complete picture for offline policy evaluation with only value function realizability. Our primary findings are threefold: 1) The sample complexity of offline policy evaluation is governed by the concentrability coefficient in an aggregated Markov Transition Model jointly determined by the function class and the offline data distribution, rather than that in the original MDP. This unifies and generalizes the ideas of Xie and Jiang (2021) and Foster et al. (2022), 2) The concentrability coefficient in the aggregated Markov Transition Model may grow exponentially with the horizon length, even when the concentrability coefficient in the original MDP is small and the offline data is admissible (i.e., the data distribution equals the occupancy measure of some policy), 3) Under value function realizability, there is a generic reduction that can convert any hard instance with admissible data to a hard instance with trajectory data, implying that trajectory data offers no extra benefits over admissible data. These three pieces jointly resolve the open problem, though each of them could be of independent interest.

Tractable Local Equilibria in Non-Concave Games

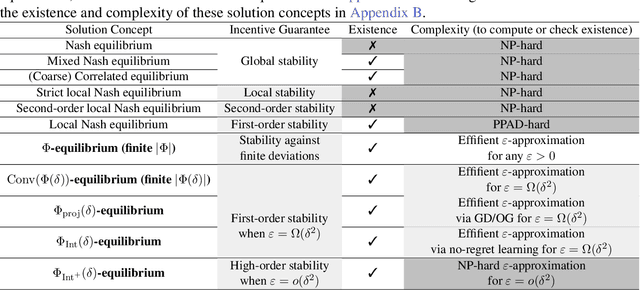
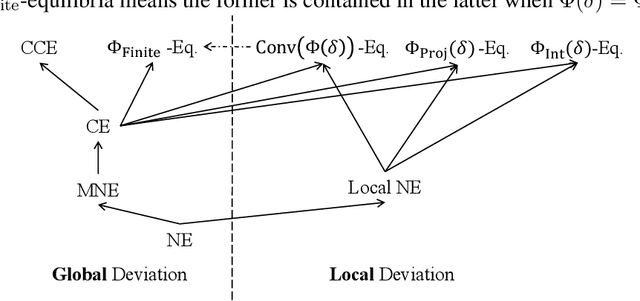
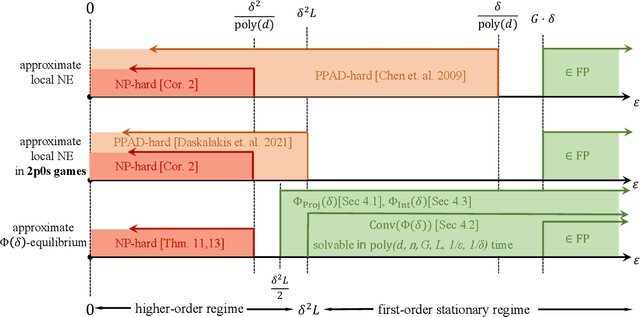
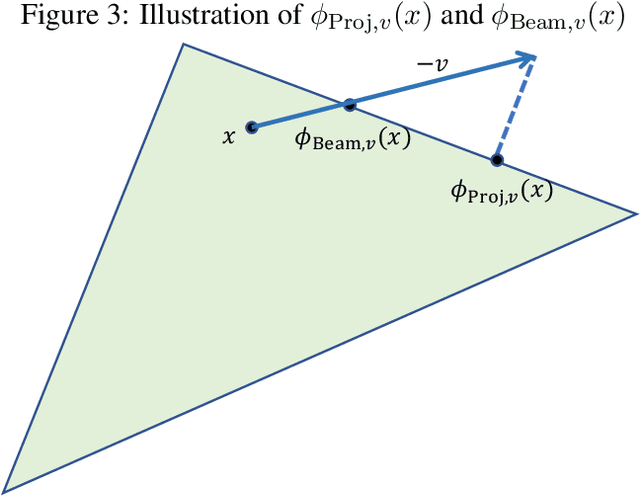
While Online Gradient Descent and other no-regret learning procedures are known to efficiently converge to coarse correlated equilibrium in games where each agent's utility is concave in their own strategy, this is not the case when the utilities are non-concave, a situation that is common in machine learning applications where the agents' strategies are parameterized by deep neural networks, or the agents' utilities are computed by a neural network, or both. Indeed, non-concave games present a host of game-theoretic and optimization challenges: (i) Nash equilibria may fail to exist; (ii) local Nash equilibria exist but are intractable; and (iii) mixed Nash, correlated, and coarse correlated equilibria have infinite support in general, and are intractable. To sidestep these challenges we propose a new solution concept, termed $(\varepsilon, \Phi(\delta))$-local equilibrium, which generalizes local Nash equilibrium in non-concave games, as well as (coarse) correlated equilibrium in concave games. Importantly, we show that two instantiations of this solution concept capture the convergence guarantees of Online Gradient Descent and no-regret learning, which we show efficiently converge to this type of equilibrium in non-concave games with smooth utilities.

Near-Optimal Policy Optimization for Correlated Equilibrium in General-Sum Markov Games

We study policy optimization algorithms for computing correlated equilibria in multi-player general-sum Markov Games. Previous results achieve $O(T^{-1/2})$ convergence rate to a correlated equilibrium and an accelerated $O(T^{-3/4})$ convergence rate to the weaker notion of coarse correlated equilibrium. In this paper, we improve both results significantly by providing an uncoupled policy optimization algorithm that attains a near-optimal $\tilde{O}(T^{-1})$ convergence rate for computing a correlated equilibrium. Our algorithm is constructed by combining two main elements (i) smooth value updates and (ii) the optimistic-follow-the-regularized-leader algorithm with the log barrier regularizer.

Towards Optimal Regret in Adversarial Linear MDPs with Bandit Feedback

We study online reinforcement learning in linear Markov decision processes with adversarial losses and bandit feedback, without prior knowledge on transitions or access to simulators. We introduce two algorithms that achieve improved regret performance compared to existing approaches. The first algorithm, although computationally inefficient, ensures a regret of $\widetilde{\mathcal{O}}\left(\sqrt{K}\right)$, where $K$ is the number of episodes. This is the first result with the optimal $K$ dependence in the considered setting. The second algorithm, which is based on the policy optimization framework, guarantees a regret of $\widetilde{\mathcal{O}}\left(K^{\frac{3}{4}} \right)$ and is computationally efficient. Both our results significantly improve over the state-of-the-art: a computationally inefficient algorithm by Kong et al. [2023] with $\widetilde{\mathcal{O}}\left(K^{\frac{4}{5}}+poly\left(\frac{1}{\lambda_{\min}}\right) \right)$ regret, for some problem-dependent constant $\lambda_{\min}$ that can be arbitrarily close to zero, and a computationally efficient algorithm by Sherman et al. [2023b] with $\widetilde{\mathcal{O}}\left(K^{\frac{6}{7}} \right)$ regret.

Bypassing the Simulator: Near-Optimal Adversarial Linear Contextual Bandits

We consider the adversarial linear contextual bandit problem, where the loss vectors are selected fully adversarially and the per-round action set (i.e. the context) is drawn from a fixed distribution. Existing methods for this problem either require access to a simulator to generate free i.i.d. contexts, achieve a sub-optimal regret no better than $\widetilde{O}(T^{\frac{5}{6}})$, or are computationally inefficient. We greatly improve these results by achieving a regret of $\widetilde{O}(\sqrt{T})$ without a simulator, while maintaining computational efficiency when the action set in each round is small. In the special case of sleeping bandits with adversarial loss and stochastic arm availability, our result answers affirmatively the open question by Saha et al. [2020] on whether there exists a polynomial-time algorithm with $poly(d)\sqrt{T}$ regret. Our approach naturally handles the case where the loss is linear up to an additive misspecification error, and our regret shows near-optimal dependence on the magnitude of the error.

Last-Iterate Convergent Policy Gradient Primal-Dual Methods for Constrained MDPs

We study the problem of computing an optimal policy of an infinite-horizon discounted constrained Markov decision process (constrained MDP). Despite the popularity of Lagrangian-based policy search methods used in practice, the oscillation of policy iterates in these methods has not been fully understood, bringing out issues such as violation of constraints and sensitivity to hyper-parameters. To fill this gap, we employ the Lagrangian method to cast a constrained MDP into a constrained saddle-point problem in which max/min players correspond to primal/dual variables, respectively, and develop two single-time-scale policy-based primal-dual algorithms with non-asymptotic convergence of their policy iterates to an optimal constrained policy. Specifically, we first propose a regularized policy gradient primal-dual (RPG-PD) method that updates the policy using an entropy-regularized policy gradient, and the dual via a quadratic-regularized gradient ascent, simultaneously. We prove that the policy primal-dual iterates of RPG-PD converge to a regularized saddle point with a sublinear rate, while the policy iterates converge sublinearly to an optimal constrained policy. We further instantiate RPG-PD in large state or action spaces by including function approximation in policy parametrization, and establish similar sublinear last-iterate policy convergence. Second, we propose an optimistic policy gradient primal-dual (OPG-PD) method that employs the optimistic gradient method to update primal/dual variables, simultaneously. We prove that the policy primal-dual iterates of OPG-PD converge to a saddle point that contains an optimal constrained policy, with a linear rate. To the best of our knowledge, this work appears to be the first non-asymptotic policy last-iterate convergence result for single-time-scale algorithms in constrained MDPs.