How Does Variance Shape the Regret in Contextual Bandits?

We consider realizable contextual bandits with general function approximation, investigating how small reward variance can lead to better-than-minimax regret bounds. Unlike in minimax bounds, we show that the eluder dimension $d_\text{elu}$$-$a complexity measure of the function class$-$plays a crucial role in variance-dependent bounds. We consider two types of adversary: (1) Weak adversary: The adversary sets the reward variance before observing the learner's action. In this setting, we prove that a regret of $\Omega(\sqrt{\min\{A,d_\text{elu}\}\Lambda}+d_\text{elu})$ is unavoidable when $d_{\text{elu}}\leq\sqrt{AT}$, where $A$ is the number of actions, $T$ is the total number of rounds, and $\Lambda$ is the total variance over $T$ rounds. For the $A\leq d_\text{elu}$ regime, we derive a nearly matching upper bound $\tilde{O}(\sqrt{A\Lambda}+d_\text{elu})$ for the special case where the variance is revealed at the beginning of each round. (2) Strong adversary: The adversary sets the reward variance after observing the learner's action. We show that a regret of $\Omega(\sqrt{d_\text{elu}\Lambda}+d_\text{elu})$ is unavoidable when $\sqrt{d_\text{elu}\Lambda}+d_\text{elu}\leq\sqrt{AT}$. In this setting, we provide an upper bound of order $\tilde{O}(d_\text{elu}\sqrt{\Lambda}+d_\text{elu})$. Furthermore, we examine the setting where the function class additionally provides distributional information of the reward, as studied by Wang et al. (2024). We demonstrate that the regret bound $\tilde{O}(\sqrt{d_\text{elu}\Lambda}+d_\text{elu})$ established in their work is unimprovable when $\sqrt{d_{\text{elu}}\Lambda}+d_\text{elu}\leq\sqrt{AT}$. However, with a slightly different definition of the total variance and with the assumption that the reward follows a Gaussian distribution, one can achieve a regret of $\tilde{O}(\sqrt{A\Lambda}+d_\text{elu})$.

Offline Reinforcement Learning: Role of State Aggregation and Trajectory Data

We revisit the problem of offline reinforcement learning with value function realizability but without Bellman completeness. Previous work by Xie and Jiang (2021) and Foster et al. (2022) left open the question whether a bounded concentrability coefficient along with trajectory-based offline data admits a polynomial sample complexity. In this work, we provide a negative answer to this question for the task of offline policy evaluation. In addition to addressing this question, we provide a rather complete picture for offline policy evaluation with only value function realizability. Our primary findings are threefold: 1) The sample complexity of offline policy evaluation is governed by the concentrability coefficient in an aggregated Markov Transition Model jointly determined by the function class and the offline data distribution, rather than that in the original MDP. This unifies and generalizes the ideas of Xie and Jiang (2021) and Foster et al. (2022), 2) The concentrability coefficient in the aggregated Markov Transition Model may grow exponentially with the horizon length, even when the concentrability coefficient in the original MDP is small and the offline data is admissible (i.e., the data distribution equals the occupancy measure of some policy), 3) Under value function realizability, there is a generic reduction that can convert any hard instance with admissible data to a hard instance with trajectory data, implying that trajectory data offers no extra benefits over admissible data. These three pieces jointly resolve the open problem, though each of them could be of independent interest.

When is Agnostic Reinforcement Learning Statistically Tractable?

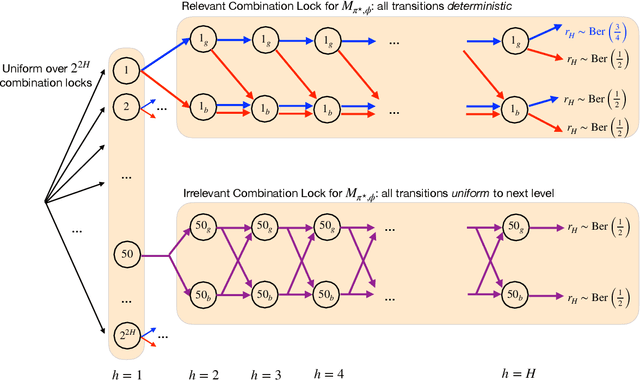
We study the problem of agnostic PAC reinforcement learning (RL): given a policy class $\Pi$, how many rounds of interaction with an unknown MDP (with a potentially large state and action space) are required to learn an $\epsilon$-suboptimal policy with respect to $\Pi$? Towards that end, we introduce a new complexity measure, called the \emph{spanning capacity}, that depends solely on the set $\Pi$ and is independent of the MDP dynamics. With a generative model, we show that for any policy class $\Pi$, bounded spanning capacity characterizes PAC learnability. However, for online RL, the situation is more subtle. We show there exists a policy class $\Pi$ with a bounded spanning capacity that requires a superpolynomial number of samples to learn. This reveals a surprising separation for agnostic learnability between generative access and online access models (as well as between deterministic/stochastic MDPs under online access). On the positive side, we identify an additional \emph{sunflower} structure, which in conjunction with bounded spanning capacity enables statistically efficient online RL via a new algorithm called POPLER, which takes inspiration from classical importance sampling methods as well as techniques for reachable-state identification and policy evaluation in reward-free exploration.

Linear Reinforcement Learning with Ball Structure Action Space

We study the problem of Reinforcement Learning (RL) with linear function approximation, i.e. assuming the optimal action-value function is linear in a known $d$-dimensional feature mapping. Unfortunately, however, based on only this assumption, the worst case sample complexity has been shown to be exponential, even under a generative model. Instead of making further assumptions on the MDP or value functions, we assume that our action space is such that there always exist playable actions to explore any direction of the feature space. We formalize this assumption as a ``ball structure'' action space, and show that being able to freely explore the feature space allows for efficient RL. In particular, we propose a sample-efficient RL algorithm (BallRL) that learns an $\epsilon$-optimal policy using only $\tilde{O}\left(\frac{H^5d^3}{\epsilon^3}\right)$ number of trajectories.

Intrinsic Dimension Estimation

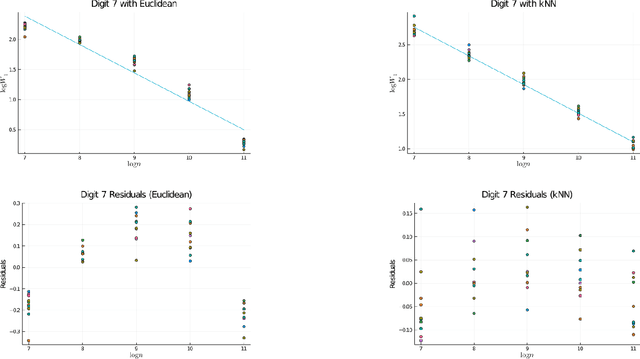
It has long been thought that high-dimensional data encountered in many practical machine learning tasks have low-dimensional structure, i.e., the manifold hypothesis holds. A natural question, thus, is to estimate the intrinsic dimension of a given population distribution from a finite sample. We introduce a new estimator of the intrinsic dimension and provide finite sample, non-asymptotic guarantees. We then apply our techniques to get new sample complexity bounds for Generative Adversarial Networks (GANs) depending only on the intrinsic dimension of the data.

Model-Based Reinforcement Learning with Value-Targeted Regression

This paper studies model-based reinforcement learning (RL) for regret minimization. We focus on finite-horizon episodic RL where the transition model $P$ belongs to a known family of models $\mathcal{P}$, a special case of which is when models in $\mathcal{P}$ take the form of linear mixtures: $P_{\theta} = \sum_{i=1}^{d} \theta_{i}P_{i}$. We propose a model based RL algorithm that is based on optimism principle: In each episode, the set of models that are `consistent' with the data collected is constructed. The criterion of consistency is based on the total squared error of that the model incurs on the task of predicting \emph{values} as determined by the last value estimate along the transitions. The next value function is then chosen by solving the optimistic planning problem with the constructed set of models. We derive a bound on the regret, which, in the special case of linear mixtures, the regret bound takes the form $\tilde{\mathcal{O}}(d\sqrt{H^{3}T})$, where $H$, $T$ and $d$ are the horizon, total number of steps and dimension of $\theta$, respectively. In particular, this regret bound is independent of the total number of states or actions, and is close to a lower bound $\Omega(\sqrt{HdT})$. For a general model family $\mathcal{P}$, the regret bound is derived using the notion of the so-called Eluder dimension proposed by Russo & Van Roy (2014).

Feature-Based Q-Learning for Two-Player Stochastic Games

Consider a two-player zero-sum stochastic game where the transition function can be embedded in a given feature space. We propose a two-player Q-learning algorithm for approximating the Nash equilibrium strategy via sampling. The algorithm is shown to find an $\epsilon$-optimal strategy using sample size linear to the number of features. To further improve its sample efficiency, we develop an accelerated algorithm by adopting techniques such as variance reduction, monotonicity preservation and two-sided strategy approximation. We prove that the algorithm is guaranteed to find an $\epsilon$-optimal strategy using no more than $\tilde{\mathcal{O}}(K/(\epsilon^{2}(1-\gamma)^{4}))$ samples with high probability, where $K$ is the number of features and $\gamma$ is a discount factor. The sample, time and space complexities of the algorithm are independent of original dimensions of the game.