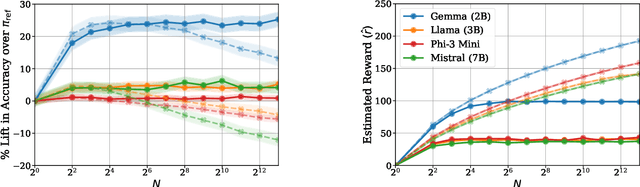
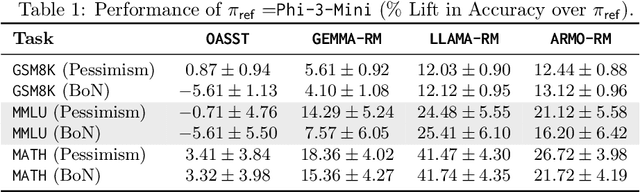
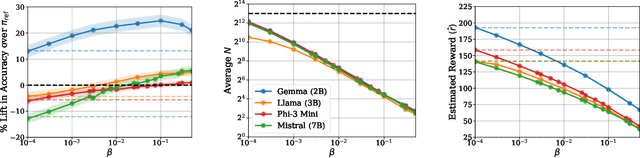
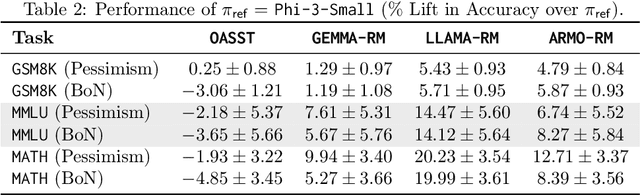
Is Best-of-N the Best of Them? Coverage, Scaling, and Optimality in Inference-Time Alignment

Inference-time computation provides an important axis for scaling language model performance, but naively scaling compute through techniques like Best-of-$N$ sampling can cause performance to degrade due to reward hacking. Toward a theoretical understanding of how to best leverage additional computation, we focus on inference-time alignment which we formalize as the problem of improving a pre-trained policy's responses for a prompt of interest, given access to an imperfect reward model. We analyze the performance of inference-time alignment algorithms in terms of (i) response quality, and (ii) compute, and provide new results that highlight the importance of the pre-trained policy's coverage over high-quality responses for performance and compute scaling: 1. We show that Best-of-$N$ alignment with an ideal choice for $N$ can achieve optimal performance under stringent notions of coverage, but provably suffers from reward hacking when $N$ is large, and fails to achieve tight guarantees under more realistic coverage conditions. 2. We introduce $\texttt{InferenceTimePessimism}$, a new algorithm which mitigates reward hacking through deliberate use of inference-time compute, implementing the principle of pessimism in the face of uncertainty via rejection sampling; we prove that its performance is optimal and does not degrade with $N$, meaning it is scaling-monotonic. We complement our theoretical results with an experimental evaluation that demonstrate the benefits of $\texttt{InferenceTimePessimism}$ across a variety of tasks and models.

A Theory of Learning with Autoregressive Chain of Thought

For a given base class of sequence-to-next-token generators, we consider learning prompt-to-answer mappings obtained by iterating a fixed, time-invariant generator for multiple steps, thus generating a chain-of-thought, and then taking the final token as the answer. We formalize the learning problems both when the chain-of-thought is observed and when training only on prompt-answer pairs, with the chain-of-thought latent. We analyze the sample and computational complexity both in terms of general properties of the base class (e.g. its VC dimension) and for specific base classes such as linear thresholds. We present a simple base class that allows for universal representability and computationally tractable chain-of-thought learning. Central to our development is that time invariance allows for sample complexity that is independent of the length of the chain-of-thought. Attention arises naturally in our construction.

Computational-Statistical Tradeoffs at the Next-Token Prediction Barrier: Autoregressive and Imitation Learning under Misspecification

Next-token prediction with the logarithmic loss is a cornerstone of autoregressive sequence modeling, but, in practice, suffers from error amplification, where errors in the model compound and generation quality degrades as sequence length $H$ increases. From a theoretical perspective, this phenomenon should not appear in well-specified settings, and, indeed, a growing body of empirical work hypothesizes that misspecification, where the learner is not sufficiently expressive to represent the target distribution, may be the root cause. Under misspecification -- where the goal is to learn as well as the best-in-class model up to a multiplicative approximation factor $C\geq 1$ -- we confirm that $C$ indeed grows with $H$ for next-token prediction, lending theoretical support to this empirical hypothesis. We then ask whether this mode of error amplification is avoidable algorithmically, computationally, or information-theoretically, and uncover inherent computational-statistical tradeoffs. We show: (1) Information-theoretically, one can avoid error amplification and achieve $C=O(1)$. (2) Next-token prediction can be made robust so as to achieve $C=\tilde O(H)$, representing moderate error amplification, but this is an inherent barrier: any next-token prediction-style objective must suffer $C=\Omega(H)$. (3) For the natural testbed of autoregressive linear models, no computationally efficient algorithm can achieve sub-polynomial approximation factor $C=e^{(\log H)^{1-\Omega(1)}}$; however, at least for binary token spaces, one can smoothly trade compute for statistical power and improve on $C=\Omega(H)$ in sub-exponential time. Our results have consequences in the more general setting of imitation learning, where the widely-used behavior cloning algorithm generalizes next-token prediction.

Self-Improvement in Language Models: The Sharpening Mechanism

Recent work in language modeling has raised the possibility of self-improvement, where a language models evaluates and refines its own generations to achieve higher performance without external feedback. It is impossible for this self-improvement to create information that is not already in the model, so why should we expect that this will lead to improved capabilities? We offer a new perspective on the capabilities of self-improvement through a lens we refer to as sharpening. Motivated by the observation that language models are often better at verifying response quality than they are at generating correct responses, we formalize self-improvement as using the model itself as a verifier during post-training in order to ``sharpen'' the model to one placing large mass on high-quality sequences, thereby amortizing the expensive inference-time computation of generating good sequences. We begin by introducing a new statistical framework for sharpening in which the learner aims to sharpen a pre-trained base policy via sample access, and establish fundamental limits. Then we analyze two natural families of self-improvement algorithms based on SFT and RLHF.

Is Behavior Cloning All You Need? Understanding Horizon in Imitation Learning

Imitation learning (IL) aims to mimic the behavior of an expert in a sequential decision making task by learning from demonstrations, and has been widely applied to robotics, autonomous driving, and autoregressive text generation. The simplest approach to IL, behavior cloning (BC), is thought to incur sample complexity with unfavorable quadratic dependence on the problem horizon, motivating a variety of different online algorithms that attain improved linear horizon dependence under stronger assumptions on the data and the learner's access to the expert. We revisit the apparent gap between offline and online IL from a learning-theoretic perspective, with a focus on general policy classes up to and including deep neural networks. Through a new analysis of behavior cloning with the logarithmic loss, we show that it is possible to achieve horizon-independent sample complexity in offline IL whenever (i) the range of the cumulative payoffs is controlled, and (ii) an appropriate notion of supervised learning complexity for the policy class is controlled. Specializing our results to deterministic, stationary policies, we show that the gap between offline and online IL is not fundamental: (i) it is possible to achieve linear dependence on horizon in offline IL under dense rewards (matching what was previously only known to be achievable in online IL); and (ii) without further assumptions on the policy class, online IL cannot improve over offline IL with the logarithmic loss, even in benign MDPs. We complement our theoretical results with experiments on standard RL tasks and autoregressive language generation to validate the practical relevance of our findings.

On the Performance of Empirical Risk Minimization with Smoothed Data

In order to circumvent statistical and computational hardness results in sequential decision-making, recent work has considered smoothed online learning, where the distribution of data at each time is assumed to have bounded likeliehood ratio with respect to a base measure when conditioned on the history. While previous works have demonstrated the benefits of smoothness, they have either assumed that the base measure is known to the learner or have presented computationally inefficient algorithms applying only in special cases. This work investigates the more general setting where the base measure is \emph{unknown} to the learner, focusing in particular on the performance of Empirical Risk Minimization (ERM) with square loss when the data are well-specified and smooth. We show that in this setting, ERM is able to achieve sublinear error whenever a class is learnable with iid data; in particular, ERM achieves error scaling as $\tilde O( \sqrt{\mathrm{comp}(\mathcal F)\cdot T} )$, where $\mathrm{comp}(\mathcal F)$ is the statistical complexity of learning $\mathcal F$ with iid data. In so doing, we prove a novel norm comparison bound for smoothed data that comprises the first sharp norm comparison for dependent data applying to arbitrary, nonlinear function classes. We complement these results with a lower bound indicating that our analysis of ERM is essentially tight, establishing a separation in the performance of ERM between smoothed and iid data.

Oracle-Efficient Differentially Private Learning with Public Data

Due to statistical lower bounds on the learnability of many function classes under privacy constraints, there has been recent interest in leveraging public data to improve the performance of private learning algorithms. In this model, algorithms must always guarantee differential privacy with respect to the private samples while also ensuring learning guarantees when the private data distribution is sufficiently close to that of the public data. Previous work has demonstrated that when sufficient public, unlabelled data is available, private learning can be made statistically tractable, but the resulting algorithms have all been computationally inefficient. In this work, we present the first computationally efficient, algorithms to provably leverage public data to learn privately whenever a function class is learnable non-privately, where our notion of computational efficiency is with respect to the number of calls to an optimization oracle for the function class. In addition to this general result, we provide specialized algorithms with improved sample complexities in the special cases when the function class is convex or when the task is binary classification.

Butterfly Effects of SGD Noise: Error Amplification in Behavior Cloning and Autoregression

This work studies training instabilities of behavior cloning with deep neural networks. We observe that minibatch SGD updates to the policy network during training result in sharp oscillations in long-horizon rewards, despite negligibly affecting the behavior cloning loss. We empirically disentangle the statistical and computational causes of these oscillations, and find them to stem from the chaotic propagation of minibatch SGD noise through unstable closed-loop dynamics. While SGD noise is benign in the single-step action prediction objective, it results in catastrophic error accumulation over long horizons, an effect we term gradient variance amplification (GVA). We show that many standard mitigation techniques do not alleviate GVA, but find an exponential moving average (EMA) of iterates to be surprisingly effective at doing so. We illustrate the generality of this phenomenon by showing the existence of GVA and its amelioration by EMA in both continuous control and autoregressive language generation. Finally, we provide theoretical vignettes that highlight the benefits of EMA in alleviating GVA and shed light on the extent to which classical convex models can help in understanding the benefits of iterate averaging in deep learning.

Imitating Complex Trajectories: Bridging Low-Level Stability and High-Level Behavior

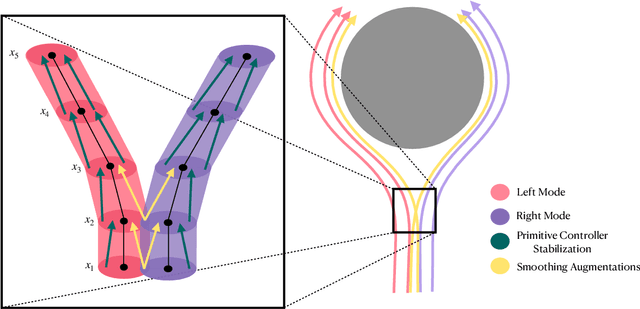
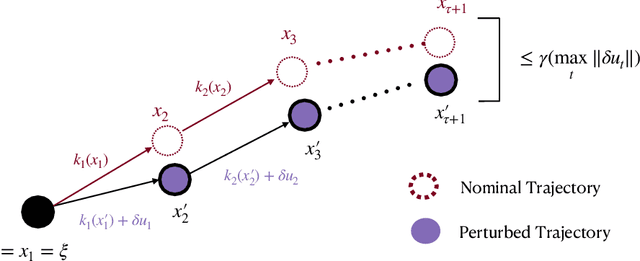
We propose a theoretical framework for studying the imitation of stochastic, non-Markovian, potentially multi-modal (i.e. "complex" ) expert demonstrations in nonlinear dynamical systems. Our framework invokes low-level controllers - either learned or implicit in position-command control - to stabilize imitation policies around expert demonstrations. We show that with (a) a suitable low-level stability guarantee and (b) a stochastic continuity property of the learned policy we call "total variation continuity" (TVC), an imitator that accurately estimates actions on the demonstrator's state distribution closely matches the demonstrator's distribution over entire trajectories. We then show that TVC can be ensured with minimal degradation of accuracy by combining a popular data-augmentation regimen with a novel algorithmic trick: adding augmentation noise at execution time. We instantiate our guarantees for policies parameterized by diffusion models and prove that if the learner accurately estimates the score of the (noise-augmented) expert policy, then the distribution of imitator trajectories is close to the demonstrator distribution in a natural optimal transport distance. Our analysis constructs intricate couplings between noise-augmented trajectories, a technique that may be of independent interest. We conclude by empirically validating our algorithmic recommendations.

Efficient Model-Free Exploration in Low-Rank MDPs

A major challenge in reinforcement learning is to develop practical, sample-efficient algorithms for exploration in high-dimensional domains where generalization and function approximation is required. Low-Rank Markov Decision Processes -- where transition probabilities admit a low-rank factorization based on an unknown feature embedding -- offer a simple, yet expressive framework for RL with function approximation, but existing algorithms are either (1) computationally intractable, or (2) reliant upon restrictive statistical assumptions such as latent variable structure, access to model-based function approximation, or reachability. In this work, we propose the first provably sample-efficient algorithm for exploration in Low-Rank MDPs that is both computationally efficient and model-free, allowing for general function approximation and requiring no additional structural assumptions. Our algorithm, VoX, uses the notion of a generalized optimal design for the feature embedding as an efficiently computable basis for exploration, performing efficient optimal design computation by interleaving representation learning and policy optimization. Our analysis -- which is appealingly simple and modular -- carefully combines several techniques, including a new reduction from optimal design computation to policy optimization based on the Frank-Wolfe method, and an improved analysis of a certain minimax representation learning objective found in prior work.