On the Complexity of Learning Sparse Functions with Statistical and Gradient Queries

The goal of this paper is to investigate the complexity of gradient algorithms when learning sparse functions (juntas). We introduce a type of Statistical Queries ($\mathsf{SQ}$), which we call Differentiable Learning Queries ($\mathsf{DLQ}$), to model gradient queries on a specified loss with respect to an arbitrary model. We provide a tight characterization of the query complexity of $\mathsf{DLQ}$ for learning the support of a sparse function over generic product distributions. This complexity crucially depends on the loss function. For the squared loss, $\mathsf{DLQ}$ matches the complexity of Correlation Statistical Queries $(\mathsf{CSQ})$--potentially much worse than $\mathsf{SQ}$. But for other simple loss functions, including the $\ell_1$ loss, $\mathsf{DLQ}$ always achieves the same complexity as $\mathsf{SQ}$. We also provide evidence that $\mathsf{DLQ}$ can indeed capture learning with (stochastic) gradient descent by showing it correctly describes the complexity of learning with a two-layer neural network in the mean field regime and linear scaling.

Exact Community Recovery (under Side Information): Optimality of Spectral Algorithms

In this paper, we study the problem of exact community recovery in general, two-community block models considering both Bernoulli and Gaussian matrix models, capturing the Stochastic Block Model, submatrix localization, and $\mathbb{Z}_2$-synchronization as special cases. We also study the settings where $side$ $information$ about community assignment labels is available, modeled as passing the true labels through a noisy channel: either the binary erasure channel (where some community labels are known while others are erased) or the binary symmetric channel (where some labels are flipped). We provide a unified analysis of the effect of side information on the information-theoretic limits of exact recovery, generalizing prior works and extending to new settings. Additionally, we design a simple but optimal spectral algorithm that incorporates side information (when present) along with the eigenvectors of the matrix observation. Using the powerful tool of entrywise eigenvector analysis [Abbe, Fan, Wang, Zhong 2020], we show that our spectral algorithm can mimic the so called $genie$-$aided$ $estimators$, where the $i^{\mathrm{th}}$ genie-aided estimator optimally computes the estimate of the $i^{\mathrm{th}}$ label, when all remaining labels are revealed by a genie. This perspective provides a unified understanding of the optimality of spectral algorithms for various exact recovery problems in a recent line of work.

The Limits and Potentials of Local SGD for Distributed Heterogeneous Learning with Intermittent Communication

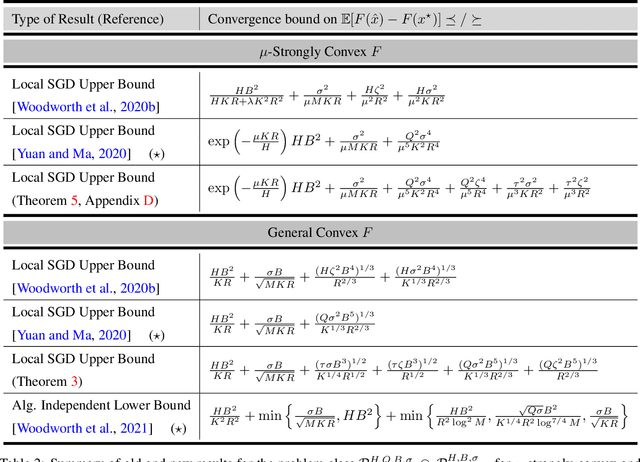
Local SGD is a popular optimization method in distributed learning, often outperforming other algorithms in practice, including mini-batch SGD. Despite this success, theoretically proving the dominance of local SGD in settings with reasonable data heterogeneity has been difficult, creating a significant gap between theory and practice. In this paper, we provide new lower bounds for local SGD under existing first-order data heterogeneity assumptions, showing that these assumptions are insufficient to prove the effectiveness of local update steps. Furthermore, under these same assumptions, we demonstrate the min-max optimality of accelerated mini-batch SGD, which fully resolves our understanding of distributed optimization for several problem classes. Our results emphasize the need for better models of data heterogeneity to understand the effectiveness of local SGD in practice. Towards this end, we consider higher-order smoothness and heterogeneity assumptions, providing new upper bounds that imply the dominance of local SGD over mini-batch SGD when data heterogeneity is low.

Noisy Interpolation Learning with Shallow Univariate ReLU Networks

We study the asymptotic overfitting behavior of interpolation with minimum norm ($\ell_2$ of the weights) two-layer ReLU networks for noisy univariate regression. We show that overfitting is tempered for the $L_1$ loss, and any $L_p$ loss for $p<2$, but catastrophic for $p\geq 2$.

Community Detection in the Hypergraph SBM: Optimal Recovery Given the Similarity Matrix

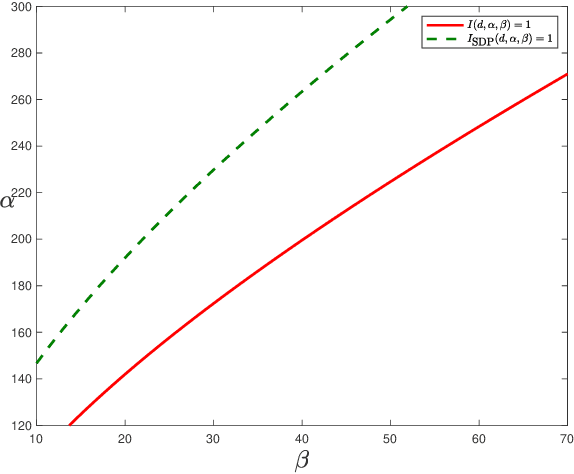
Community detection is a fundamental problem in network science. In this paper, we consider community detection in hypergraphs drawn from the $hypergraph$ $stochastic$ $block$ $model$ (HSBM), with a focus on exact community recovery. We study the performance of polynomial-time algorithms for community detection in a case where the full hypergraph is unknown. Instead, we are provided a $similarity$ $matrix$ $W$, where $W_{ij}$ reports the number of hyperedges containing both $i$ and $j$. Under this information model, Kim, Bandeira, and Goemans [KBG18] determined the information-theoretic threshold for exact recovery, and proposed a semidefinite programming relaxation which they conjectured to be optimal. In this paper, we confirm this conjecture. We also show that a simple, highly efficient spectral algorithm is optimal, establishing the spectral algorithm as the method of choice. Our analysis of the spectral algorithm crucially relies on strong $entrywise$ bounds on the eigenvectors of $W$. Our bounds are inspired by the work of Abbe, Fan, Wang, and Zhong [AFWZ20], who developed entrywise bounds for eigenvectors of symmetric matrices with independent entries. Despite the complex dependency structure in similarity matrices, we prove similar entrywise guarantees.