Exact Community Recovery (under Side Information): Optimality of Spectral Algorithms

In this paper, we study the problem of exact community recovery in general, two-community block models considering both Bernoulli and Gaussian matrix models, capturing the Stochastic Block Model, submatrix localization, and $\mathbb{Z}_2$-synchronization as special cases. We also study the settings where $side$ $information$ about community assignment labels is available, modeled as passing the true labels through a noisy channel: either the binary erasure channel (where some community labels are known while others are erased) or the binary symmetric channel (where some labels are flipped). We provide a unified analysis of the effect of side information on the information-theoretic limits of exact recovery, generalizing prior works and extending to new settings. Additionally, we design a simple but optimal spectral algorithm that incorporates side information (when present) along with the eigenvectors of the matrix observation. Using the powerful tool of entrywise eigenvector analysis [Abbe, Fan, Wang, Zhong 2020], we show that our spectral algorithm can mimic the so called $genie$-$aided$ $estimators$, where the $i^{\mathrm{th}}$ genie-aided estimator optimally computes the estimate of the $i^{\mathrm{th}}$ label, when all remaining labels are revealed by a genie. This perspective provides a unified understanding of the optimality of spectral algorithms for various exact recovery problems in a recent line of work.

Community Detection in the Hypergraph SBM: Optimal Recovery Given the Similarity Matrix

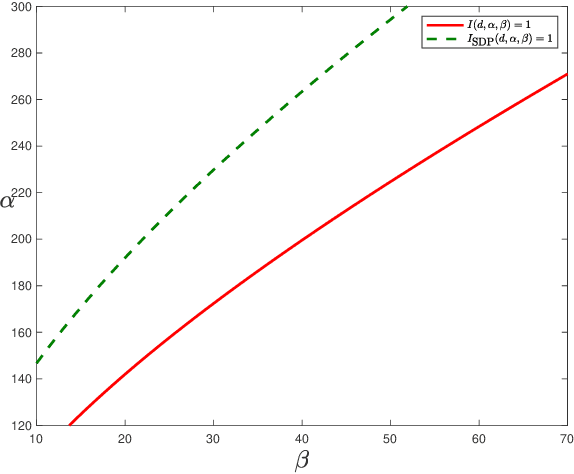
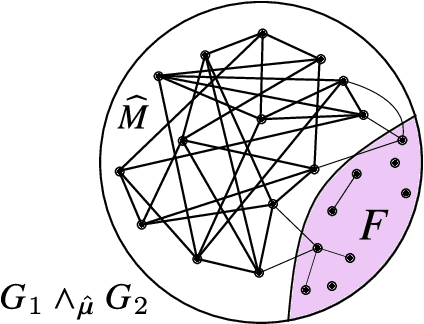
Community detection is a fundamental problem in network science. In this paper, we consider community detection in hypergraphs drawn from the $hypergraph$ $stochastic$ $block$ $model$ (HSBM), with a focus on exact community recovery. We study the performance of polynomial-time algorithms for community detection in a case where the full hypergraph is unknown. Instead, we are provided a $similarity$ $matrix$ $W$, where $W_{ij}$ reports the number of hyperedges containing both $i$ and $j$. Under this information model, Kim, Bandeira, and Goemans [KBG18] determined the information-theoretic threshold for exact recovery, and proposed a semidefinite programming relaxation which they conjectured to be optimal. In this paper, we confirm this conjecture. We also show that a simple, highly efficient spectral algorithm is optimal, establishing the spectral algorithm as the method of choice. Our analysis of the spectral algorithm crucially relies on strong $entrywise$ bounds on the eigenvectors of $W$. Our bounds are inspired by the work of Abbe, Fan, Wang, and Zhong [AFWZ20], who developed entrywise bounds for eigenvectors of symmetric matrices with independent entries. Despite the complex dependency structure in similarity matrices, we prove similar entrywise guarantees.

Exact Community Recovery in Correlated Stochastic Block Models

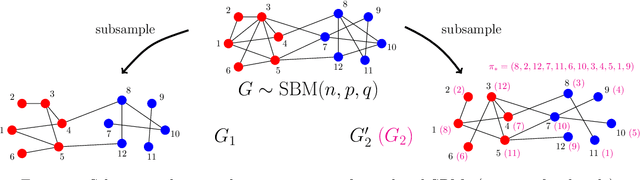
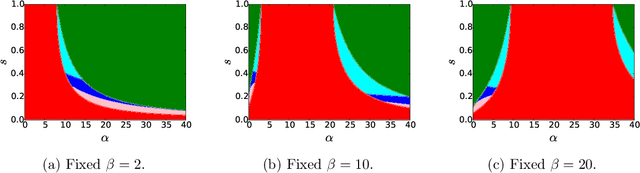
We consider the problem of learning latent community structure from multiple correlated networks. We study edge-correlated stochastic block models with two balanced communities, focusing on the regime where the average degree is logarithmic in the number of vertices. Our main result derives the precise information-theoretic threshold for exact community recovery using multiple correlated graphs. This threshold captures the interplay between the community recovery and graph matching tasks. In particular, we uncover and characterize a region of the parameter space where exact community recovery is possible using multiple correlated graphs, even though (1) this is information-theoretically impossible using a single graph and (2) exact graph matching is also information-theoretically impossible. In this regime, we develop a novel algorithm that carefully synthesizes algorithms from the community recovery and graph matching literatures.

Spectral Algorithms Optimally Recover (Censored) Planted Dense Subgraphs

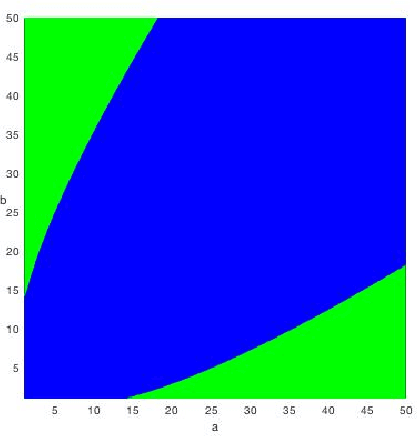
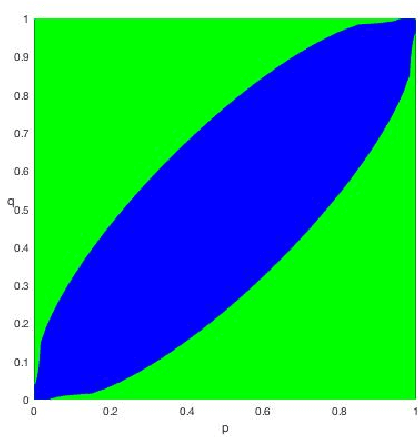
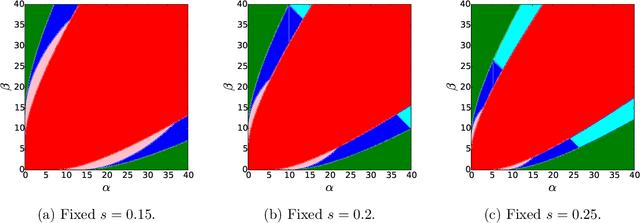
We study spectral algorithms for the planted dense subgraph problem (PDS), as well as for a censored variant (CPDS) of PDS, where the edge statuses are missing at random. More precisely, in the PDS model, we consider $n$ vertices and a random subset of vertices $S^{\star}$ of size $\Omega(n)$, such that two vertices share an edge with probability $p$ if both of them are in $S^{\star}$, and all other edges are present with probability $q$, independently. The goal is to recover $S^{\star}$ from one observation of the network. In the CPDS model, edge statuses are revealed with probability $\frac{t \log n}{n}$. For the PDS model, we show that a simple spectral algorithm based on the top two eigenvectors of the adjacency matrix can recover $S^{\star}$ up to the information theoretic threshold. Prior work by Hajek, Wu and Xu required a less efficient SDP based algorithm to recover $S^{\star}$ up to the information theoretic threshold. For the CDPS model, we obtain the information theoretic limit for the recovery problem, and further show that a spectral algorithm based on a special matrix called the signed adjacency matrix recovers $S^{\star}$ up to the information theoretic threshold.