Miklos Z. Racz
Exact Community Recovery in Correlated Stochastic Block Models
Mar 29, 2022
Abstract:We consider the problem of learning latent community structure from multiple correlated networks. We study edge-correlated stochastic block models with two balanced communities, focusing on the regime where the average degree is logarithmic in the number of vertices. Our main result derives the precise information-theoretic threshold for exact community recovery using multiple correlated graphs. This threshold captures the interplay between the community recovery and graph matching tasks. In particular, we uncover and characterize a region of the parameter space where exact community recovery is possible using multiple correlated graphs, even though (1) this is information-theoretically impossible using a single graph and (2) exact graph matching is also information-theoretically impossible. In this regime, we develop a novel algorithm that carefully synthesizes algorithms from the community recovery and graph matching literatures.
Correlated Stochastic Block Models: Exact Graph Matching with Applications to Recovering Communities
Jul 14, 2021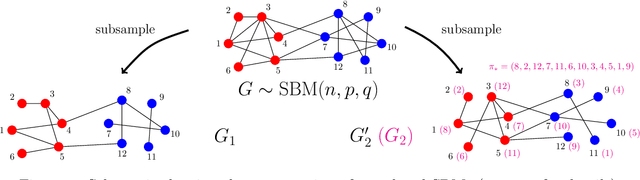
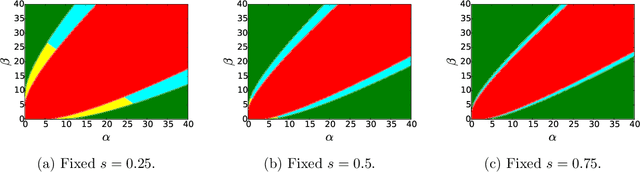
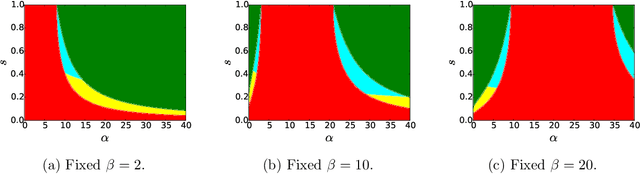
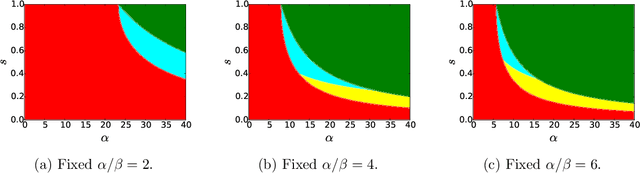
Abstract:We consider the task of learning latent community structure from multiple correlated networks. First, we study the problem of learning the latent vertex correspondence between two edge-correlated stochastic block models, focusing on the regime where the average degree is logarithmic in the number of vertices. We derive the precise information-theoretic threshold for exact recovery: above the threshold there exists an estimator that outputs the true correspondence with probability close to 1, while below it no estimator can recover the true correspondence with probability bounded away from 0. As an application of our results, we show how one can exactly recover the latent communities using multiple correlated graphs in parameter regimes where it is information-theoretically impossible to do so using just a single graph.
Approximate Trace Reconstruction
Dec 16, 2020
Abstract:In the usual trace reconstruction problem, the goal is to exactly reconstruct an unknown string of length $n$ after it passes through a deletion channel many times independently, producing a set of traces (i.e., random subsequences of the string). We consider the relaxed problem of approximate reconstruction. Here, the goal is to output a string that is close to the original one in edit distance while using much fewer traces than is needed for exact reconstruction. We present several algorithms that can approximately reconstruct strings that belong to certain classes, where the estimate is within $n/\mathrm{polylog}(n)$ edit distance, and where we only use $\mathrm{polylog}(n)$ traces (or sometimes just a single trace). These classes contain strings that require a linear number of traces for exact reconstruction and which are quite different from a typical random string. From a technical point of view, our algorithms approximately reconstruct consecutive substrings of the unknown string by aligning dense regions of traces and using a run of a suitable length to approximate each region. To complement our algorithms, we present a general black-box lower bound for approximate reconstruction, building on a lower bound for distinguishing between two candidate input strings in the worst case. In particular, this shows that approximating to within $n^{1/3 - \delta}$ edit distance requires $n^{1 + 3\delta/2}/\mathrm{polylog}(n)$ traces for $0< \delta < 1/3$ in the worst case.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge