Correlated Stochastic Block Models: Exact Graph Matching with Applications to Recovering Communities
Paper and Code
Jul 14, 2021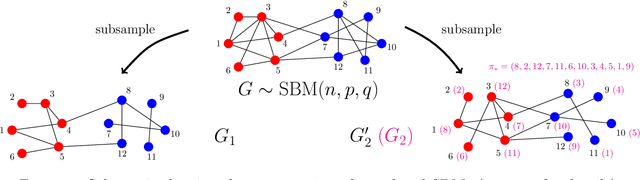
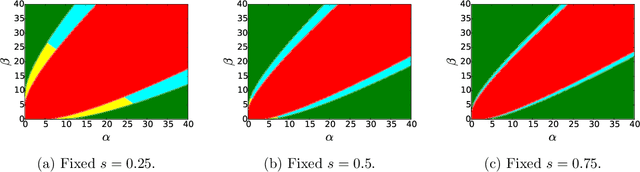
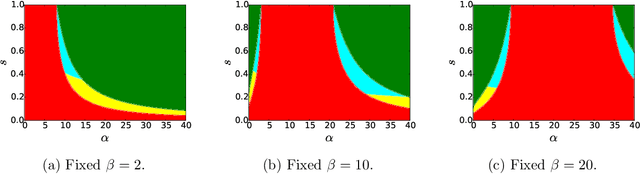
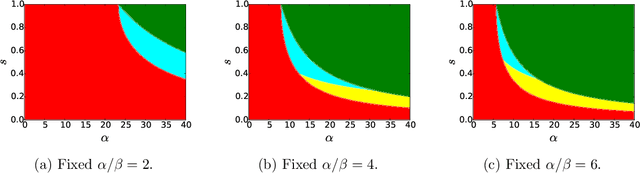
We consider the task of learning latent community structure from multiple correlated networks. First, we study the problem of learning the latent vertex correspondence between two edge-correlated stochastic block models, focusing on the regime where the average degree is logarithmic in the number of vertices. We derive the precise information-theoretic threshold for exact recovery: above the threshold there exists an estimator that outputs the true correspondence with probability close to 1, while below it no estimator can recover the true correspondence with probability bounded away from 0. As an application of our results, we show how one can exactly recover the latent communities using multiple correlated graphs in parameter regimes where it is information-theoretically impossible to do so using just a single graph.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge