Matching Correlated Inhomogeneous Random Graphs using the $k$-core Estimator

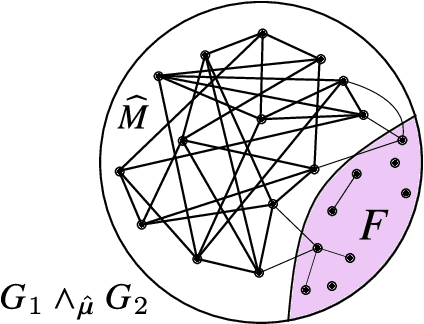
We consider the task of estimating the latent vertex correspondence between two edge-correlated random graphs with generic, inhomogeneous structure. We study the so-called \emph{$k$-core estimator}, which outputs a vertex correspondence that induces a large, common subgraph of both graphs which has minimum degree at least $k$. We derive sufficient conditions under which the $k$-core estimator exactly or partially recovers the latent vertex correspondence. Finally, we specialize our general framework to derive new results on exact and partial recovery in correlated stochastic block models, correlated Chung-Lu graphs, and correlated random geometric graphs.

Recovering the Graph Underlying Networked Dynamical Systems under Partial Observability: A Deep Learning Approach

We study the problem of graph structure identification, i.e., of recovering the graph of dependencies among time series. We model these time series data as components of the state of linear stochastic networked dynamical systems. We assume partial observability, where the state evolution of only a subset of nodes comprising the network is observed. We devise a new feature vector computed from the observed time series and prove that these features are linearly separable, i.e., there exists a hyperplane that separates the cluster of features associated with connected pairs of nodes from those associated with disconnected pairs. This renders the features amenable to train a variety of classifiers to perform causal inference. In particular, we use these features to train Convolutional Neural Networks (CNNs). The resulting causal inference mechanism outperforms state-of-the-art counterparts w.r.t. sample-complexity. The trained CNNs generalize well over structurally distinct networks (dense or sparse) and noise-level profiles. Remarkably, they also generalize well to real-world networks while trained over a synthetic network (realization of a random graph). Finally, the proposed method consistently reconstructs the graph in a pairwise manner, that is, by deciding if an edge or arrow is present or absent in each pair of nodes, from the corresponding time series of each pair. This fits the framework of large-scale systems, where observation or processing of all nodes in the network is prohibitive.

Exact Community Recovery in Correlated Stochastic Block Models

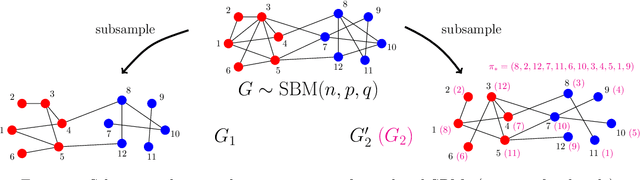
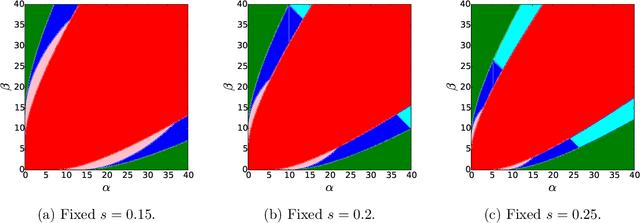
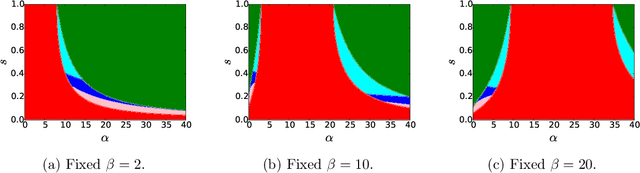
We consider the problem of learning latent community structure from multiple correlated networks. We study edge-correlated stochastic block models with two balanced communities, focusing on the regime where the average degree is logarithmic in the number of vertices. Our main result derives the precise information-theoretic threshold for exact community recovery using multiple correlated graphs. This threshold captures the interplay between the community recovery and graph matching tasks. In particular, we uncover and characterize a region of the parameter space where exact community recovery is possible using multiple correlated graphs, even though (1) this is information-theoretically impossible using a single graph and (2) exact graph matching is also information-theoretically impossible. In this regime, we develop a novel algorithm that carefully synthesizes algorithms from the community recovery and graph matching literatures.

Correlated Stochastic Block Models: Exact Graph Matching with Applications to Recovering Communities

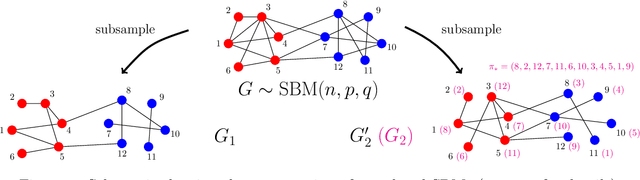
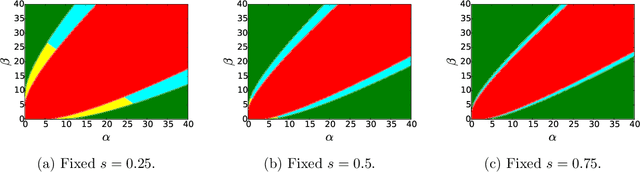
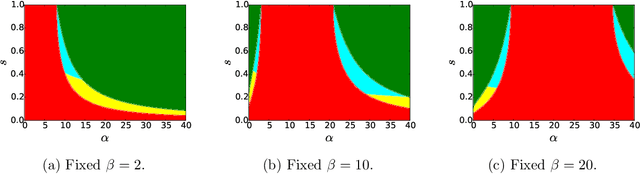
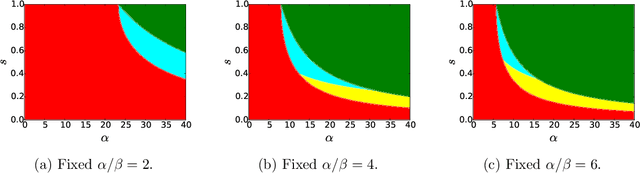
We consider the task of learning latent community structure from multiple correlated networks. First, we study the problem of learning the latent vertex correspondence between two edge-correlated stochastic block models, focusing on the regime where the average degree is logarithmic in the number of vertices. We derive the precise information-theoretic threshold for exact recovery: above the threshold there exists an estimator that outputs the true correspondence with probability close to 1, while below it no estimator can recover the true correspondence with probability bounded away from 0. As an application of our results, we show how one can exactly recover the latent communities using multiple correlated graphs in parameter regimes where it is information-theoretically impossible to do so using just a single graph.