Exact Community Recovery in Correlated Stochastic Block Models
Paper and Code
Mar 29, 2022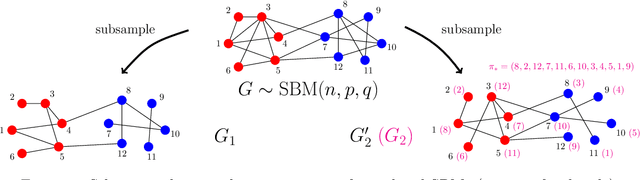
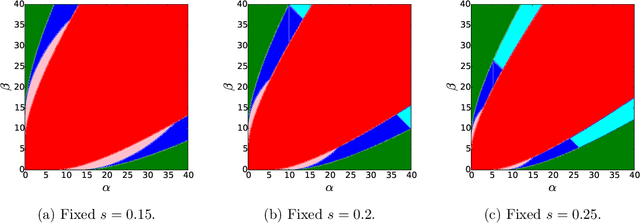
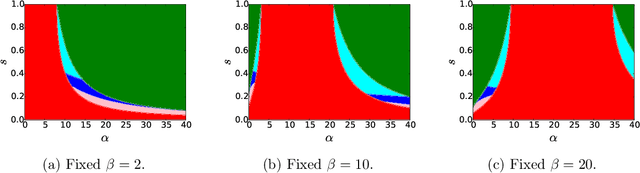
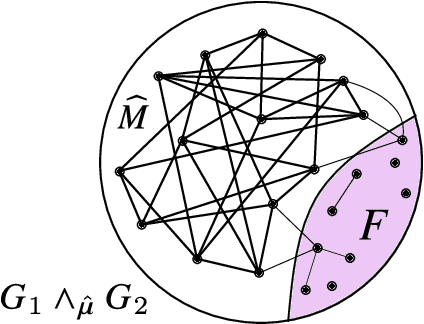
We consider the problem of learning latent community structure from multiple correlated networks. We study edge-correlated stochastic block models with two balanced communities, focusing on the regime where the average degree is logarithmic in the number of vertices. Our main result derives the precise information-theoretic threshold for exact community recovery using multiple correlated graphs. This threshold captures the interplay between the community recovery and graph matching tasks. In particular, we uncover and characterize a region of the parameter space where exact community recovery is possible using multiple correlated graphs, even though (1) this is information-theoretically impossible using a single graph and (2) exact graph matching is also information-theoretically impossible. In this regime, we develop a novel algorithm that carefully synthesizes algorithms from the community recovery and graph matching literatures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge