Inferring the Graph of Networked Dynamical Systems under Partial Observability and Spatially Colored Noise

In a Networked Dynamical System (NDS), each node is a system whose dynamics are coupled with the dynamics of neighboring nodes. The global dynamics naturally builds on this network of couplings and it is often excited by a noise input with nontrivial structure. The underlying network is unknown in many applications and should be inferred from observed data. We assume: i) Partial observability -- time series data is only available over a subset of the nodes; ii) Input noise -- it is correlated across distinct nodes while temporally independent, i.e., it is spatially colored. We present a feasibility condition on the noise correlation structure wherein there exists a consistent network inference estimator to recover the underlying fundamental dependencies among the observed nodes. Further, we describe a structure identification algorithm that exhibits competitive performance across distinct regimes of network connectivity, observability, and noise correlation.

Learning the Causal Structure of Networked Dynamical Systems under Latent Nodes and Structured Noise

This paper considers learning the hidden causal network of a linear networked dynamical system (NDS) from the time series data at some of its nodes -- partial observability. The dynamics of the NDS are driven by colored noise that generates spurious associations across pairs of nodes, rendering the problem much harder. To address the challenge of noise correlation and partial observability, we assign to each pair of nodes a feature vector computed from the time series data of observed nodes. The feature embedding is engineered to yield structural consistency: there exists an affine hyperplane that consistently partitions the set of features, separating the feature vectors corresponding to connected pairs of nodes from those corresponding to disconnected pairs. The causal inference problem is thus addressed via clustering the designed features. We demonstrate with simple baseline supervised methods the competitive performance of the proposed causal inference mechanism under broad connectivity regimes and noise correlation levels, including a real world network. Further, we devise novel technical guarantees of structural consistency for linear NDS under the considered regime.

Recovering the Graph Underlying Networked Dynamical Systems under Partial Observability: A Deep Learning Approach

We study the problem of graph structure identification, i.e., of recovering the graph of dependencies among time series. We model these time series data as components of the state of linear stochastic networked dynamical systems. We assume partial observability, where the state evolution of only a subset of nodes comprising the network is observed. We devise a new feature vector computed from the observed time series and prove that these features are linearly separable, i.e., there exists a hyperplane that separates the cluster of features associated with connected pairs of nodes from those associated with disconnected pairs. This renders the features amenable to train a variety of classifiers to perform causal inference. In particular, we use these features to train Convolutional Neural Networks (CNNs). The resulting causal inference mechanism outperforms state-of-the-art counterparts w.r.t. sample-complexity. The trained CNNs generalize well over structurally distinct networks (dense or sparse) and noise-level profiles. Remarkably, they also generalize well to real-world networks while trained over a synthetic network (realization of a random graph). Finally, the proposed method consistently reconstructs the graph in a pairwise manner, that is, by deciding if an edge or arrow is present or absent in each pair of nodes, from the corresponding time series of each pair. This fits the framework of large-scale systems, where observation or processing of all nodes in the network is prohibitive.

PSO-Convolutional Neural Networks with Heterogeneous Learning Rate

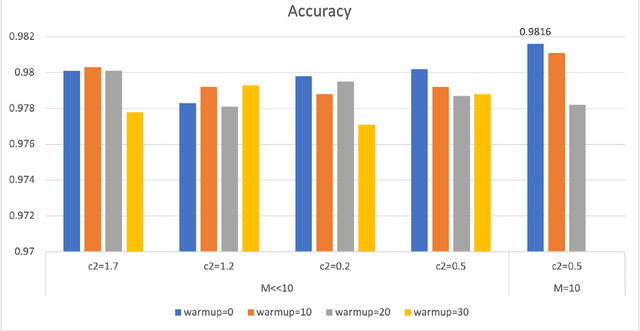
Convolutional Neural Networks (ConvNets) have been candidly deployed in the scope of computer vision and related fields. Nevertheless, the dynamics of training of these neural networks lie still elusive: it is hard and computationally expensive to train them. A myriad of architectures and training strategies have been proposed to overcome this challenge and address several problems in image processing such as speech, image and action recognition as well as object detection. In this article, we propose a novel Particle Swarm Optimization (PSO) based training for ConvNets. In such framework, the vector of weights of each ConvNet is typically cast as the position of a particle in phase space whereby PSO collaborative dynamics intertwines with Stochastic Gradient Descent (SGD) in order to boost training performance and generalization. Our approach goes as follows: i) [warm-up phase] each ConvNet is trained independently via SGD; ii) [collaborative phase] ConvNets share among themselves their current vector of weights (or particle-position) along with their gradient estimates of the Loss function. Distinct step sizes are coined by distinct ConvNets. By properly blending ConvNets with large (possibly random) step-sizes along with more conservative ones, we propose an algorithm with competitive performance with respect to other PSO-based approaches on Cifar-10 (accuracy of 98.31%). These accuracy levels are obtained by resorting to only four ConvNets -- such results are expected to scale with the number of collaborative ConvNets accordingly. We make our source codes available for download https://github.com/leonlha/PSO-ConvNet-Dynamics.

Inverse Graph Learning over Optimization Networks

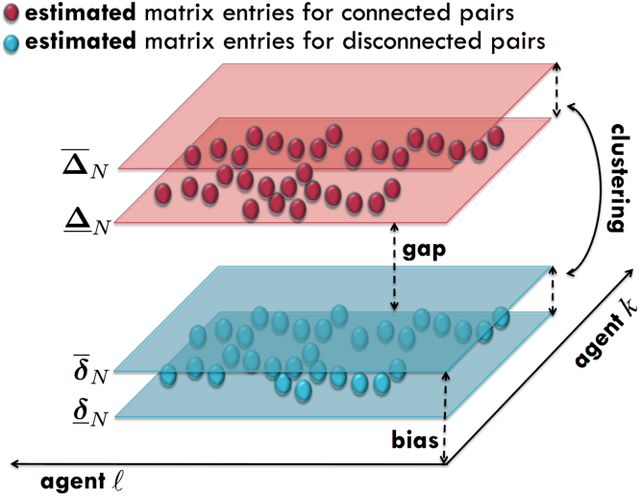
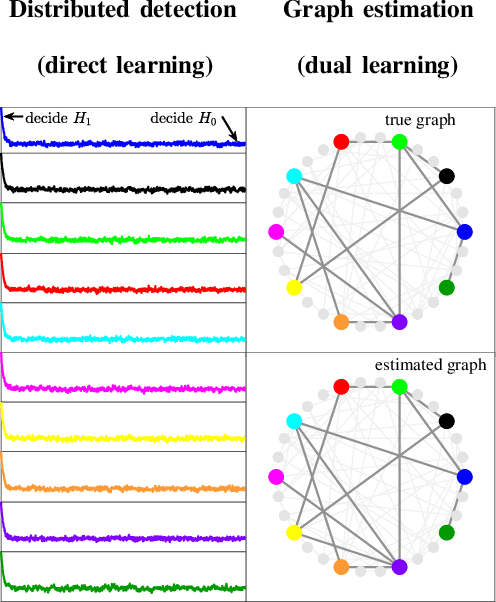
Many inferential and learning tasks can be accomplished efficiently by means of distributed optimization algorithms where the network topology plays a critical role in driving the local interactions among neighboring agents. There is a large body of literature examining the effect of the graph structure on the performance of optimization strategies. In this article, we examine the inverse problem and consider the reverse question: How much information does observing the behavior at the nodes convey about the underlying network structure used for optimization? Over large-scale networks, the difficulty of addressing such inverse questions (or problems) is compounded by the fact that usually only a limited portion of nodes can be probed, giving rise to a second important question: Despite the presence of several unobserved nodes, are partial and local observations still sufficient to discover the graph linking the probed nodes? The article surveys recent advances on this inverse learning problem and related questions. Examples of applications are provided to illustrate how the interplay between graph learning and distributed optimization arises in practice, e.g., in cognitive engineered systems such as distributed detection, or in other real-world problems such as the mechanism of opinion formation over social networks and the mechanism of coordination in biological networks. A unifying framework for examining the reconstruction error will be described, which allows to devise and examine various estimation strategies enabling successful graph learning. The relevance of specific network attributes, such as sparsity versus density of connections, and node degree concentration, is discussed in relation to the topology inference goal. It is shown how universal (i.e., data-driven) clustering algorithms can be exploited to solve the graph learning problem.

Learning Erdős-Rényi Graphs under Partial Observations: Concentration or Sparsity?

This work examines the problem of graph learning over a diffusion network when data can be collected from a limited portion of the network (partial observability). While most works in the literature rely on a degree of sparsity to provide guarantees of consistent graph recovery, our analysis moves away from this condition and includes the demanding setting of dense connectivity. We ascertain that suitable estimators of the combination matrix (i.e., the matrix that quantifies the pairwise interaction between nodes) possess an identifiability gap that enables the discrimination between connected and disconnected nodes. Fundamental conditions are established under which the subgraph of monitored nodes can be recovered, with high probability as the network size increases, through universal clustering algorithms. This claim is proved for three matrix estimators: i) the Granger estimator that adapts to the partial observability setting the solution that is optimal under full observability ; ii) the one-lag correlation matrix; and iii) the residual estimator based on the difference between two consecutive time samples. Comparison among the estimators is performed through illustrative examples that reveal how estimators that are not optimal in the full observability regime can outperform the Granger estimator in the partial observability regime. The analysis reveals that the fundamental property enabling consistent graph learning is the statistical concentration of node degrees, rather than the sparsity of connections.