Warm-starting Push-Relabel

Push-Relabel is one of the most celebrated network flow algorithms. Maintaining a pre-flow that saturates a cut, it enjoys better theoretical and empirical running time than other flow algorithms, such as Ford-Fulkerson. In practice, Push-Relabel is even faster than what theoretical guarantees can promise, in part because of the use of good heuristics for seeding and updating the iterative algorithm. However, it remains unclear how to run Push-Relabel on an arbitrary initialization that is not necessarily a pre-flow or cut-saturating. We provide the first theoretical guarantees for warm-starting Push-Relabel with a predicted flow, where our learning-augmented version benefits from fast running time when the predicted flow is close to an optimal flow, while maintaining robust worst-case guarantees. Interestingly, our algorithm uses the gap relabeling heuristic, which has long been employed in practice, even though prior to our work there was no rigorous theoretical justification for why it can lead to run-time improvements. We then provide experiments that show our warm-started Push-Relabel also works well in practice.

Lower Bounds on the Total Variation Distance Between Mixtures of Two Gaussians

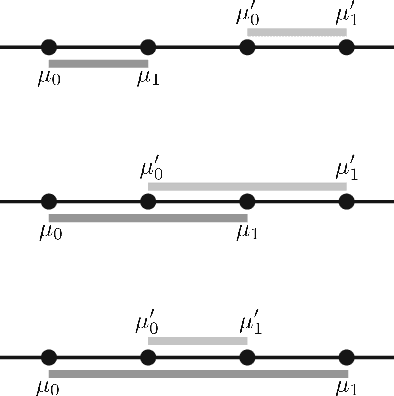
Mixtures of high dimensional Gaussian distributions have been studied extensively in statistics and learning theory. While the total variation distance appears naturally in the sample complexity of distribution learning, it is analytically difficult to obtain tight lower bounds for mixtures. Exploiting a connection between total variation distance and the characteristic function of the mixture, we provide fairly tight functional approximations. This enables us to derive new lower bounds on the total variation distance between pairs of two-component Gaussian mixtures that have a shared covariance matrix.

Approximate Trace Reconstruction

In the usual trace reconstruction problem, the goal is to exactly reconstruct an unknown string of length $n$ after it passes through a deletion channel many times independently, producing a set of traces (i.e., random subsequences of the string). We consider the relaxed problem of approximate reconstruction. Here, the goal is to output a string that is close to the original one in edit distance while using much fewer traces than is needed for exact reconstruction. We present several algorithms that can approximately reconstruct strings that belong to certain classes, where the estimate is within $n/\mathrm{polylog}(n)$ edit distance, and where we only use $\mathrm{polylog}(n)$ traces (or sometimes just a single trace). These classes contain strings that require a linear number of traces for exact reconstruction and which are quite different from a typical random string. From a technical point of view, our algorithms approximately reconstruct consecutive substrings of the unknown string by aligning dense regions of traces and using a run of a suitable length to approximate each region. To complement our algorithms, we present a general black-box lower bound for approximate reconstruction, building on a lower bound for distinguishing between two candidate input strings in the worst case. In particular, this shows that approximating to within $n^{1/3 - \delta}$ edit distance requires $n^{1 + 3\delta/2}/\mathrm{polylog}(n)$ traces for $0< \delta < 1/3$ in the worst case.