Regret minimization in Linear Bandits with offline data via extended D-optimal exploration

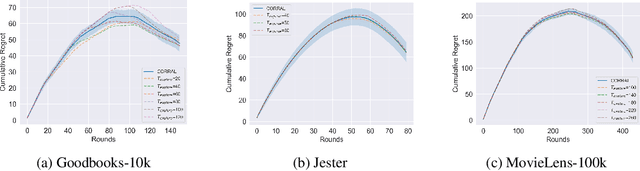
We consider the problem of online regret minimization in linear bandits with access to prior observations (offline data) from the underlying bandit model. There are numerous applications where extensive offline data is often available, such as in recommendation systems, online advertising. Consequently, this problem has been studied intensively in recent literature. Our algorithm, Offline-Online Phased Elimination (OOPE), effectively incorporates the offline data to substantially reduce the online regret compared to prior work. To leverage offline information prudently, OOPE uses an extended D-optimal design within each exploration phase. OOPE achieves an online regret is $\tilde{O}(\sqrt{\deff T \log \left(|\mathcal{A}|T\right)}+d^2)$. $\deff \leq d)$ is the effective problem dimension which measures the number of poorly explored directions in offline data and depends on the eigen-spectrum $(\lambda_k)_{k \in [d]}$ of the Gram matrix of the offline data. The eigen-spectrum $(\lambda_k)_{k \in [d]}$ is a quantitative measure of the \emph{quality} of offline data. If the offline data is poorly explored ($\deff \approx d$), we recover the established regret bounds for purely online setting while, when offline data is abundant ($\Toff >> T$) and well-explored ($\deff = o(1) $), the online regret reduces substantially. Additionally, we provide the first known minimax regret lower bounds in this setting that depend explicitly on the quality of the offline data. These lower bounds establish the optimality of our algorithm in regimes where offline data is either well-explored or poorly explored. Finally, by using a Frank-Wolfe approximation to the extended optimal design we further improve the $O(d^{2})$ term to $O\left(\frac{d^{2}}{\deff} \min \{ \deff,1\} \right)$, which can be substantial in high dimensions with moderate quality of offline data $\deff = \Omega(1)$.

From Selection to Generation: A Survey of LLM-based Active Learning

Active Learning (AL) has been a powerful paradigm for improving model efficiency and performance by selecting the most informative data points for labeling and training. In recent active learning frameworks, Large Language Models (LLMs) have been employed not only for selection but also for generating entirely new data instances and providing more cost-effective annotations. Motivated by the increasing importance of high-quality data and efficient model training in the era of LLMs, we present a comprehensive survey on LLM-based Active Learning. We introduce an intuitive taxonomy that categorizes these techniques and discuss the transformative roles LLMs can play in the active learning loop. We further examine the impact of AL on LLM learning paradigms and its applications across various domains. Finally, we identify open challenges and propose future research directions. This survey aims to serve as an up-to-date resource for researchers and practitioners seeking to gain an intuitive understanding of LLM-based AL techniques and deploy them to new applications.

PromptRefine: Enhancing Few-Shot Performance on Low-Resource Indic Languages with Example Selection from Related Example Banks

Large Language Models (LLMs) have recently demonstrated impressive few-shot learning capabilities through in-context learning (ICL). However, ICL performance is highly dependent on the choice of few-shot demonstrations, making the selection of the most optimal examples a persistent research challenge. This issue is further amplified in low-resource Indic languages, where the scarcity of ground-truth data complicates the selection process. In this work, we propose PromptRefine, a novel Alternating Minimization approach for example selection that improves ICL performance on low-resource Indic languages. PromptRefine leverages auxiliary example banks from related high-resource Indic languages and employs multi-task learning techniques to align language-specific retrievers, enabling effective cross-language retrieval. Additionally, we incorporate diversity in the selected examples to enhance generalization and reduce bias. Through comprehensive evaluations on four text generation tasks -- Cross-Lingual Question Answering, Multilingual Question Answering, Machine Translation, and Cross-Lingual Summarization using state-of-the-art LLMs such as LLAMA-3.1-8B, LLAMA-2-7B, Qwen-2-7B, and Qwen-2.5-7B, we demonstrate that PromptRefine significantly outperforms existing frameworks for retrieving examples.

Annotation Efficiency: Identifying Hard Samples via Blocked Sparse Linear Bandits

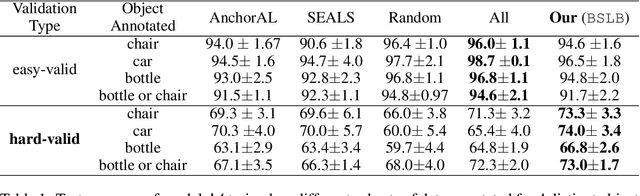
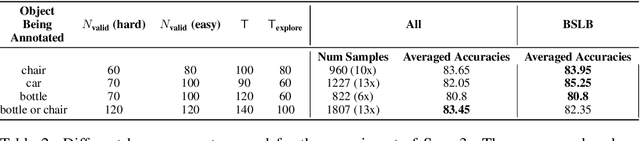
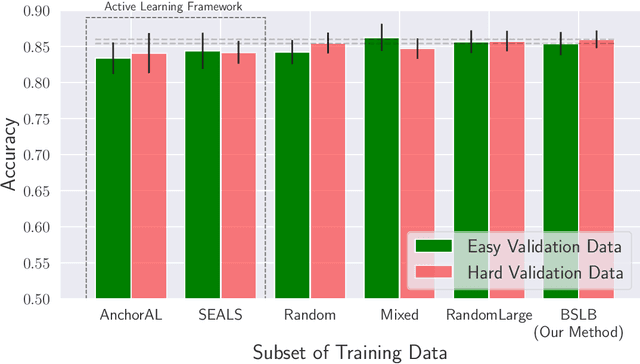
This paper considers the problem of annotating datapoints using an expert with only a few annotation rounds in a label-scarce setting. We propose soliciting reliable feedback on difficulty in annotating a datapoint from the expert in addition to ground truth label. Existing literature in active learning or coreset selection turns out to be less relevant to our setting since they presume the existence of a reliable trained model, which is absent in the label-scarce regime. However, the literature on coreset selection emphasizes the presence of difficult data points in the training set to perform supervised learning in downstream tasks (Mindermann et al., 2022). Therefore, for a given fixed annotation budget of $\mathsf{T}$ rounds, we model the sequential decision-making problem of which (difficult) datapoints to choose for annotation in a sparse linear bandits framework with the constraint that no arm can be pulled more than once (blocking constraint). With mild assumptions on the datapoints, our (computationally efficient) Explore-Then-Commit algorithm BSLB achieves a regret guarantee of $\widetilde{\mathsf{O}}(k^{\frac{1}{3}} \mathsf{T}^{\frac{2}{3}} +k^{-\frac{1}{2}} \beta_k + k^{-\frac{1}{12}} \beta_k^{\frac{1}{2}}\mathsf{T}^{\frac{5}{6}})$ where the unknown parameter vector has tail magnitude $\beta_k$ at sparsity level $k$. To this end, we show offline statistical guarantees of Lasso estimator with mild Restricted Eigenvalue (RE) condition that is also robust to sparsity. Finally, we propose a meta-algorithm C-BSLB that does not need knowledge of the optimal sparsity parameters at a no-regret cost. We demonstrate the efficacy of our BSLB algorithm for annotation in the label-scarce setting for an image classification task on the PASCAL-VOC dataset, where we use real-world annotation difficulty scores.

Near-Optimal Streaming Heavy-Tailed Statistical Estimation with Clipped SGD

We consider the problem of high-dimensional heavy-tailed statistical estimation in the streaming setting, which is much harder than the traditional batch setting due to memory constraints. We cast this problem as stochastic convex optimization with heavy tailed stochastic gradients, and prove that the widely used Clipped-SGD algorithm attains near-optimal sub-Gaussian statistical rates whenever the second moment of the stochastic gradient noise is finite. More precisely, with $T$ samples, we show that Clipped-SGD, for smooth and strongly convex objectives, achieves an error of $\sqrt{\frac{\mathsf{Tr}(\Sigma)+\sqrt{\mathsf{Tr}(\Sigma)\|\Sigma\|_2}\log(\frac{\log(T)}{\delta})}{T}}$ with probability $1-\delta$, where $\Sigma$ is the covariance of the clipped gradient. Note that the fluctuations (depending on $\frac{1}{\delta}$) are of lower order than the term $\mathsf{Tr}(\Sigma)$. This improves upon the current best rate of $\sqrt{\frac{\mathsf{Tr}(\Sigma)\log(\frac{1}{\delta})}{T}}$ for Clipped-SGD, known only for smooth and strongly convex objectives. Our results also extend to smooth convex and lipschitz convex objectives. Key to our result is a novel iterative refinement strategy for martingale concentration, improving upon the PAC-Bayes approach of Catoni and Giulini.

FiRST: Finetuning Router-Selective Transformers for Input-Adaptive Latency Reduction

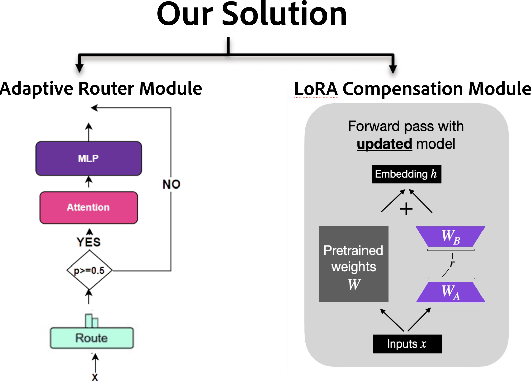
Auto-regressive Large Language Models (LLMs) demonstrate remarkable performance across domanins such as vision and language processing. However, due to sequential processing through a stack of transformer layers, autoregressive decoding faces significant computation/latency challenges, particularly in resource constrained environments like mobile and edge devices. Existing approaches in literature that aim to improve latency via skipping layers have two distinct flavors - 1) Early exit 2) Input-agnostic heuristics where tokens exit at pre-determined layers irrespective of input sequence. Both the above strategies have limitations - the former cannot be applied to handle KV Caching necessary for speed-ups in modern framework and the latter does not capture the variation in layer importance across tasks or more generally, across input sequences. To address both limitations, we propose FIRST, an algorithm that reduces inference latency by using layer-specific routers to select a subset of transformer layers adaptively for each input sequence - the prompt (during prefill stage) decides which layers will be skipped during decoding. FIRST preserves compatibility with KV caching enabling faster inference while being quality-aware. FIRST is model-agnostic and can be easily enabled on any pre-trained LLM. We further improve performance by incorporating LoRA adapters for fine-tuning on external datasets, enhancing task-specific accuracy while maintaining latency benefits. Our approach reveals that input adaptivity is critical - indeed, different task-specific middle layers play a crucial role in evolving hidden representations depending on task. Extensive experiments show that FIRST significantly reduces latency while retaining competitive performance (as compared to baselines), making our approach an efficient solution for LLM deployment in low-resource environments.

Online Matrix Completion: A Collaborative Approach with Hott Items

We investigate the low rank matrix completion problem in an online setting with ${M}$ users, ${N}$ items, ${T}$ rounds, and an unknown rank-$r$ reward matrix ${R}\in \mathbb{R}^{{M}\times {N}}$. This problem has been well-studied in the literature and has several applications in practice. In each round, we recommend ${S}$ carefully chosen distinct items to every user and observe noisy rewards. In the regime where ${M},{N} >> {T}$, we propose two distinct computationally efficient algorithms for recommending items to users and analyze them under the benign \emph{hott items} assumption.1) First, for ${S}=1$, under additional incoherence/smoothness assumptions on ${R}$, we propose the phased algorithm \textsc{PhasedClusterElim}. Our algorithm obtains a near-optimal per-user regret of $\tilde{O}({N}{M}^{-1}(\Delta^{-1}+\Delta_{{hott}}^{-2}))$ where $\Delta_{{hott}},\Delta$ are problem-dependent gap parameters with $\Delta_{{hott}} >> \Delta$ almost always. 2) Second, we consider a simplified setting with ${S}=r$ where we make significantly milder assumptions on ${R}$. Here, we introduce another phased algorithm, \textsc{DeterminantElim}, to derive a regret guarantee of $\widetilde{O}({N}{M}^{-1/r}\Delta_{det}^{-1}))$ where $\Delta_{{det}}$ is another problem-dependent gap. Both algorithms crucially use collaboration among users to jointly eliminate sub-optimal items for groups of users successively in phases, but with distinctive and novel approaches.

Blocked Collaborative Bandits: Online Collaborative Filtering with Per-Item Budget Constraints

We consider the problem of \emph{blocked} collaborative bandits where there are multiple users, each with an associated multi-armed bandit problem. These users are grouped into \emph{latent} clusters such that the mean reward vectors of users within the same cluster are identical. Our goal is to design algorithms that maximize the cumulative reward accrued by all the users over time, under the \emph{constraint} that no arm of a user is pulled more than $\mathsf{B}$ times. This problem has been originally considered by \cite{Bresler:2014}, and designing regret-optimal algorithms for it has since remained an open problem. In this work, we propose an algorithm called \texttt{B-LATTICE} (Blocked Latent bAndiTs via maTrIx ComplEtion) that collaborates across users, while simultaneously satisfying the budget constraints, to maximize their cumulative rewards. Theoretically, under certain reasonable assumptions on the latent structure, with $\mathsf{M}$ users, $\mathsf{N}$ arms, $\mathsf{T}$ rounds per user, and $\mathsf{C}=O(1)$ latent clusters, \texttt{B-LATTICE} achieves a per-user regret of $\widetilde{O}(\sqrt{\mathsf{T}(1 + \mathsf{N}\mathsf{M}^{-1})}$ under a budget constraint of $\mathsf{B}=\Theta(\log \mathsf{T})$. These are the first sub-linear regret bounds for this problem, and match the minimax regret bounds when $\mathsf{B}=\mathsf{T}$. Empirically, we demonstrate that our algorithm has superior performance over baselines even when $\mathsf{B}=1$. \texttt{B-LATTICE} runs in phases where in each phase it clusters users into groups and collaborates across users within a group to quickly learn their reward models.

Optimal Algorithms for Latent Bandits with Cluster Structure

We consider the problem of latent bandits with cluster structure where there are multiple users, each with an associated multi-armed bandit problem. These users are grouped into \emph{latent} clusters such that the mean reward vectors of users within the same cluster are identical. At each round, a user, selected uniformly at random, pulls an arm and observes a corresponding noisy reward. The goal of the users is to maximize their cumulative rewards. This problem is central to practical recommendation systems and has received wide attention of late \cite{gentile2014online, maillard2014latent}. Now, if each user acts independently, then they would have to explore each arm independently and a regret of $\Omega(\sqrt{\mathsf{MNT}})$ is unavoidable, where $\mathsf{M}, \mathsf{N}$ are the number of arms and users, respectively. Instead, we propose LATTICE (Latent bAndiTs via maTrIx ComplEtion) which allows exploitation of the latent cluster structure to provide the minimax optimal regret of $\widetilde{O}(\sqrt{(\mathsf{M}+\mathsf{N})\mathsf{T}})$, when the number of clusters is $\widetilde{O}(1)$. This is the first algorithm to guarantee such a strong regret bound. LATTICE is based on a careful exploitation of arm information within a cluster while simultaneously clustering users. Furthermore, it is computationally efficient and requires only $O(\log{\mathsf{T}})$ calls to an offline matrix completion oracle across all $\mathsf{T}$ rounds.

Improved Support Recovery in Universal One-bit Compressed Sensing

One-bit compressed sensing (1bCS) is an extremely quantized signal acquisition method that has been proposed and studied rigorously in the past decade. In 1bCS, linear samples of a high dimensional signal are quantized to only one bit per sample (sign of the measurement). Assuming the original signal vector to be sparse, existing results in 1bCS either aim to find the support of the vector, or approximate the signal allowing a small error. The focus of this paper is support recovery, which often also computationally facilitate approximate signal recovery. A {\em universal} measurement matrix for 1bCS refers to one set of measurements that work for all sparse signals. With universality, it is known that $\tilde{\Theta}(k^2)$ 1bCS measurements are necessary and sufficient for support recovery (where $k$ denotes the sparsity). To improve the dependence on sparsity from quadratic to linear, in this work we propose approximate support recovery (allowing $\epsilon>0$ proportion of errors), and superset recovery (allowing $\epsilon$ proportion of false positives). We show that the first type of recovery is possible with $\tilde{O}(k/\epsilon)$ measurements, while the later type of recovery, more challenging, is possible with $\tilde{O}(\max\{k/\epsilon,k^{3/2}\})$ measurements. We also show that in both cases $\Omega(k/\epsilon)$ measurements would be necessary for universal recovery. Improved results are possible if we consider universal recovery within a restricted class of signals, such as rational signals, or signals with bounded dynamic range. In both cases superset recovery is possible with only $\tilde{O}(k/\epsilon)$ measurements. Other results on universal but approximate support recovery are also provided in this paper. All of our main recovery algorithms are simple and polynomial-time.