Why DPO is a Misspecified Estimator and How to Fix It

Direct alignment algorithms such as Direct Preference Optimization (DPO) fine-tune models based on preference data, using only supervised learning instead of two-stage reinforcement learning with human feedback (RLHF). We show that DPO encodes a statistical estimation problem over reward functions induced by a parametric policy class. When the true reward function that generates preferences cannot be realized via the policy class, DPO becomes misspecified, resulting in failure modes such as preference order reversal, worsening of policy reward, and high sensitivity to the input preference data distribution. On the other hand, we study the local behavior of two-stage RLHF for a parametric class and relate it to a natural gradient step in policy space. Our fine-grained geometric characterization allows us to propose AuxDPO, which introduces additional auxiliary variables in the DPO loss function to help move towards the RLHF solution in a principled manner and mitigate the misspecification in DPO. We empirically demonstrate the superior performance of AuxDPO on didactic bandit settings as well as LLM alignment tasks.

KITE: Kernelized and Information Theoretic Exemplars for In-Context Learning

In-context learning (ICL) has emerged as a powerful paradigm for adapting large language models (LLMs) to new and data-scarce tasks using only a few carefully selected task-specific examples presented in the prompt. However, given the limited context size of LLMs, a fundamental question arises: Which examples should be selected to maximize performance on a given user query? While nearest-neighbor-based methods like KATE have been widely adopted for this purpose, they suffer from well-known drawbacks in high-dimensional embedding spaces, including poor generalization and a lack of diversity. In this work, we study this problem of example selection in ICL from a principled, information theory-driven perspective. We first model an LLM as a linear function over input embeddings and frame the example selection task as a query-specific optimization problem: selecting a subset of exemplars from a larger example bank that minimizes the prediction error on a specific query. This formulation departs from traditional generalization-focused learning theoretic approaches by targeting accurate prediction for a specific query instance. We derive a principled surrogate objective that is approximately submodular, enabling the use of a greedy algorithm with an approximation guarantee. We further enhance our method by (i) incorporating the kernel trick to operate in high-dimensional feature spaces without explicit mappings, and (ii) introducing an optimal design-based regularizer to encourage diversity in the selected examples. Empirically, we demonstrate significant improvements over standard retrieval methods across a suite of classification tasks, highlighting the benefits of structure-aware, diverse example selection for ICL in real-world, label-scarce scenarios.

DP-NCB: Privacy Preserving Fair Bandits

Multi-armed bandit algorithms are fundamental tools for sequential decision-making under uncertainty, with widespread applications across domains such as clinical trials and personalized decision-making. As bandit algorithms are increasingly deployed in these socially sensitive settings, it becomes critical to protect user data privacy and ensure fair treatment across decision rounds. While prior work has independently addressed privacy and fairness in bandit settings, the question of whether both objectives can be achieved simultaneously has remained largely open. Existing privacy-preserving bandit algorithms typically optimize average regret, a utilitarian measure, whereas fairness-aware approaches focus on minimizing Nash regret, which penalizes inequitable reward distributions, but often disregard privacy concerns. To bridge this gap, we introduce Differentially Private Nash Confidence Bound (DP-NCB)-a novel and unified algorithmic framework that simultaneously ensures $\epsilon$-differential privacy and achieves order-optimal Nash regret, matching known lower bounds up to logarithmic factors. The framework is sufficiently general to operate under both global and local differential privacy models, and is anytime, requiring no prior knowledge of the time horizon. We support our theoretical guarantees with simulations on synthetic bandit instances, showing that DP-NCB incurs substantially lower Nash regret than state-of-the-art baselines. Our results offer a principled foundation for designing bandit algorithms that are both privacy-preserving and fair, making them suitable for high-stakes, socially impactful applications.

Right Now, Wrong Then: Non-Stationary Direct Preference Optimization under Preference Drift

Reinforcement learning from human feedback (RLHF) aligns Large Language Models (LLMs) with human preferences. However, these preferences can often change over time due to external factors (e.g. environment change and societal influence). Consequently, what was wrong then might be right now. Current preference optimization algorithms do not account for temporal preference drift in their modeling, which can lead to severe misalignment. To address this limitation, we use a Dynamic Bradley-Terry model that models preferences via time-dependent reward functions, and propose Non-Stationary Direct Preference Optimisation (NS-DPO). By introducing a discount parameter in the loss function, NS-DPO applies exponential weighting, which proportionally focuses learning on more time-relevant datapoints. We theoretically analyse the convergence of NS-DPO in the offline setting, providing upper bounds on the estimation error caused by non-stationary preferences. Finally, we demonstrate the effectiveness of NS-DPO1 for fine-tuning LLMs in scenarios with drifting preferences. By simulating preference drift using renowned reward models and modifying popular LLM datasets accordingly, we show that NS-DPO fine-tuned LLMs remain robust under non-stationarity, significantly outperforming baseline algorithms that ignore temporal preference changes, without sacrificing performance in stationary cases.

Provably Robust DPO: Aligning Language Models with Noisy Feedback

Learning from preference-based feedback has recently gained traction as a promising approach to align language models with human interests. While these aligned generative models have demonstrated impressive capabilities across various tasks, their dependence on high-quality human preference data poses a bottleneck in practical applications. Specifically, noisy (incorrect and ambiguous) preference pairs in the dataset might restrict the language models from capturing human intent accurately. While practitioners have recently proposed heuristics to mitigate the effect of noisy preferences, a complete theoretical understanding of their workings remain elusive. In this work, we aim to bridge this gap by by introducing a general framework for policy optimization in the presence of random preference flips. We focus on the direct preference optimization (DPO) algorithm in particular since it assumes that preferences adhere to the Bradley-Terry-Luce (BTL) model, raising concerns about the impact of noisy data on the learned policy. We design a novel loss function, which de-bias the effect of noise on average, making a policy trained by minimizing that loss robust to the noise. Under log-linear parameterization of the policy class and assuming good feature coverage of the SFT policy, we prove that the sub-optimality gap of the proposed robust DPO (rDPO) policy compared to the optimal policy is of the order $O(\frac{1}{1-2\epsilon}\sqrt{\frac{d}{n}})$, where $\epsilon < 1/2$ is flip rate of labels, $d$ is policy parameter dimension and $n$ is size of dataset. Our experiments on IMDb sentiment generation and Anthropic's helpful-harmless dataset show that rDPO is robust to noise in preference labels compared to vanilla DPO and other heuristics proposed by practitioners.

Provably Sample Efficient RLHF via Active Preference Optimization

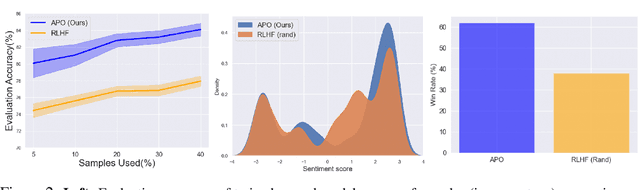
Reinforcement Learning from Human Feedback (RLHF) is pivotal in aligning Large Language Models (LLMs) with human preferences. While these aligned generative models have demonstrated impressive capabilities across various tasks, the dependence on high-quality human preference data poses a costly bottleneck in practical implementation of RLHF. Hence better and adaptive strategies for data collection is needed. To this end, we frame RLHF as a contextual preference bandit problem with prompts as contexts and show that the naive way of collecting preference data by choosing prompts uniformly at random leads to a policy that suffers an $\Omega(1)$ suboptimality gap in rewards. Then we propose $\textit{Active Preference Optimization}$ ($\texttt{APO}$), an algorithm that actively selects prompts to collect preference data. Under the Bradley-Terry-Luce (BTL) preference model, \texttt{APO} achieves sample efficiency without compromising on policy performance. We show that given a sample budget of $T$, the suboptimality gap of a policy learned via $\texttt{APO}$ scales as $O(1/\sqrt{T})$. Next, we propose a compute-efficient batch version of $\texttt{APO}$ with minor modification and evaluate its performance in practice. Experimental evaluations on a human preference dataset validate \texttt{APO}'s efficacy as a sample-efficient and practical solution to data collection for RLHF, facilitating alignment of LLMs with human preferences in a cost-effective and scalable manner.

GAR-meets-RAG Paradigm for Zero-Shot Information Retrieval

Given a query and a document corpus, the information retrieval (IR) task is to output a ranked list of relevant documents. Combining large language models (LLMs) with embedding-based retrieval models, recent work shows promising results on the zero-shot retrieval problem, i.e., no access to labeled data from the target domain. Two such popular paradigms are generation-augmented retrieval or GAR (generate additional context for the query and then retrieve), and retrieval-augmented generation or RAG (retrieve relevant documents as context and then generate answers). The success of these paradigms hinges on (i) high-recall retrieval models, which are difficult to obtain in the zero-shot setting, and (ii) high-precision (re-)ranking models which typically need a good initialization. In this work, we propose a novel GAR-meets-RAG recurrence formulation that overcomes the challenges of existing paradigms. Our method iteratively improves retrieval (via GAR) and rewrite (via RAG) stages in the zero-shot setting. A key design principle is that the rewrite-retrieval stages improve the recall of the system and a final re-ranking stage improves the precision. We conduct extensive experiments on zero-shot passage retrieval benchmarks, BEIR and TREC-DL. Our method establishes a new state-of-the-art in the BEIR benchmark, outperforming previous best results in Recall@100 and nDCG@10 metrics on 6 out of 8 datasets, with up to 17% relative gains over the previous best.

Differentially Private Reward Estimation with Preference Feedback

Learning from preference-based feedback has recently gained considerable traction as a promising approach to align generative models with human interests. Instead of relying on numerical rewards, the generative models are trained using reinforcement learning with human feedback (RLHF). These approaches first solicit feedback from human labelers typically in the form of pairwise comparisons between two possible actions, then estimate a reward model using these comparisons, and finally employ a policy based on the estimated reward model. An adversarial attack in any step of the above pipeline might reveal private and sensitive information of human labelers. In this work, we adopt the notion of label differential privacy (DP) and focus on the problem of reward estimation from preference-based feedback while protecting privacy of each individual labelers. Specifically, we consider the parametric Bradley-Terry-Luce (BTL) model for such pairwise comparison feedback involving a latent reward parameter $\theta^* \in \mathbb{R}^d$. Within a standard minimax estimation framework, we provide tight upper and lower bounds on the error in estimating $\theta^*$ under both local and central models of DP. We show, for a given privacy budget $\epsilon$ and number of samples $n$, that the additional cost to ensure label-DP under local model is $\Theta \big(\frac{1}{ e^\epsilon-1}\sqrt{\frac{d}{n}}\big)$, while it is $\Theta\big(\frac{\text{poly}(d)}{\epsilon n} \big)$ under the weaker central model. We perform simulations on synthetic data that corroborate these theoretical results.

Differentially Private Episodic Reinforcement Learning with Heavy-tailed Rewards

In this paper, we study the problem of (finite horizon tabular) Markov decision processes (MDPs) with heavy-tailed rewards under the constraint of differential privacy (DP). Compared with the previous studies for private reinforcement learning that typically assume rewards are sampled from some bounded or sub-Gaussian distributions to ensure DP, we consider the setting where reward distributions have only finite $(1+v)$-th moments with some $v \in (0,1]$. By resorting to robust mean estimators for rewards, we first propose two frameworks for heavy-tailed MDPs, i.e., one is for value iteration and another is for policy optimization. Under each framework, we consider both joint differential privacy (JDP) and local differential privacy (LDP) models. Based on our frameworks, we provide regret upper bounds for both JDP and LDP cases and show that the moment of distribution and privacy budget both have significant impacts on regrets. Finally, we establish a lower bound of regret minimization for heavy-tailed MDPs in JDP model by reducing it to the instance-independent lower bound of heavy-tailed multi-armed bandits in DP model. We also show the lower bound for the problem in LDP by adopting some private minimax methods. Our results reveal that there are fundamental differences between the problem of private RL with sub-Gaussian and that with heavy-tailed rewards.

On Differentially Private Federated Linear Contextual Bandits

We consider cross-silo federated linear contextual bandit (LCB) problem under differential privacy. In this setting, multiple silos or agents interact with the local users and communicate via a central server to realize collaboration while without sacrificing each user's privacy. We identify two issues in the state-of-the-art algorithm of \cite{dubey2020differentially}: (i) failure of claimed privacy protection and (ii) noise miscalculation in regret bound. To resolve these issues, we take a two-step principled approach. First, we design an algorithmic framework consisting of a generic federated LCB algorithm and flexible privacy protocols. Then, leveraging the proposed framework, we study federated LCBs under two different privacy constraints. We first establish privacy and regret guarantees under silo-level local differential privacy, which fix the issues present in state-of-the-art algorithm. To further improve the regret performance, we next consider shuffle model of differential privacy, under which we show that our algorithm can achieve nearly ``optimal'' regret without a trusted server. We accomplish this via two different schemes -- one relies on a new result on privacy amplification via shuffling for DP mechanisms and another one leverages the integration of a shuffle protocol for vector sum into the tree-based mechanism, both of which might be of independent interest. Finally, we support our theoretical results with numerical evaluations over contextual bandit instances generated from both synthetic and real-life data.