Reliable Policy Iteration: Performance Robustness Across Architecture and Environment Perturbations

In a recent work, we proposed Reliable Policy Iteration (RPI), that restores policy iteration's monotonicity-of-value-estimates property to the function approximation setting. Here, we assess the robustness of RPI's empirical performance on two classical control tasks -- CartPole and Inverted Pendulum -- under changes to neural network and environmental parameters. Relative to DQN, Double DQN, DDPG, TD3, and PPO, RPI reaches near-optimal performance early and sustains this policy as training proceeds. Because deep RL methods are often hampered by sample inefficiency, training instability, and hyperparameter sensitivity, our results highlight RPI's promise as a more reliable alternative.

Why DPO is a Misspecified Estimator and How to Fix It

Direct alignment algorithms such as Direct Preference Optimization (DPO) fine-tune models based on preference data, using only supervised learning instead of two-stage reinforcement learning with human feedback (RLHF). We show that DPO encodes a statistical estimation problem over reward functions induced by a parametric policy class. When the true reward function that generates preferences cannot be realized via the policy class, DPO becomes misspecified, resulting in failure modes such as preference order reversal, worsening of policy reward, and high sensitivity to the input preference data distribution. On the other hand, we study the local behavior of two-stage RLHF for a parametric class and relate it to a natural gradient step in policy space. Our fine-grained geometric characterization allows us to propose AuxDPO, which introduces additional auxiliary variables in the DPO loss function to help move towards the RLHF solution in a principled manner and mitigate the misspecification in DPO. We empirically demonstrate the superior performance of AuxDPO on didactic bandit settings as well as LLM alignment tasks.

Reliable Critics: Monotonic Improvement and Convergence Guarantees for Reinforcement Learning

Despite decades of research, it remains challenging to correctly use Reinforcement Learning (RL) algorithms with function approximation. A prime example is policy iteration, whose fundamental guarantee of monotonic improvement collapses even under linear function approximation. To address this issue, we introduce Reliable Policy Iteration (RPI). It replaces the common projection or Bellman-error minimization during policy evaluation with a Bellman-based constrained optimization. We prove that not only does RPI confer textbook monotonicity on its value estimates but these estimates also lower bound the true return. Also, their limit partially satisfies the unprojected Bellman equation, emphasizing RPI's natural fit within RL. RPI is the first algorithm with such monotonicity and convergence guarantees under function approximation. For practical use, we provide a model-free variant of RPI that amounts to a novel critic. It can be readily integrated into primary model-free PI implementations such as DQN and DDPG. In classical control tasks, such RPI-enhanced variants consistently maintain their lower-bound guarantee while matching or surpassing the performance of all baseline methods.

Towards Reliable Alignment: Uncertainty-aware RLHF

Recent advances in aligning Large Language Models with human preferences have benefited from larger reward models and better preference data. However, most of these methodologies rely on the accuracy of the reward model. The reward models used in Reinforcement Learning with Human Feedback (RLHF) are typically learned from small datasets using stochastic optimization algorithms, making them prone to high variability. We illustrate the inconsistencies between reward models empirically on numerous open-source datasets. We theoretically show that the fluctuation of the reward models can be detrimental to the alignment problem because the derived policies are more overfitted to the reward model and, hence, are riskier if the reward model itself is uncertain. We use concentration of measure to motivate an uncertainty-aware, conservative algorithm for policy optimization. We show that such policies are more risk-averse in the sense that they are more cautious of uncertain rewards. We theoretically prove that our proposed methodology has less risk than the vanilla method. We corroborate our theoretical results with experiments based on designing an ensemble of reward models. We use this ensemble of reward models to align a language model using our methodology and observe that our empirical findings match our theoretical predictions.

Testing the Feasibility of Linear Programs with Bandit Feedback

While the recent literature has seen a surge in the study of constrained bandit problems, all existing methods for these begin by assuming the feasibility of the underlying problem. We initiate the study of testing such feasibility assumptions, and in particular address the problem in the linear bandit setting, thus characterising the costs of feasibility testing for an unknown linear program using bandit feedback. Concretely, we test if $\exists x: Ax \ge 0$ for an unknown $A \in \mathbb{R}^{m \times d}$, by playing a sequence of actions $x_t\in \mathbb{R}^d$, and observing $Ax_t + \mathrm{noise}$ in response. By identifying the hypothesis as determining the sign of the value of a minimax game, we construct a novel test based on low-regret algorithms and a nonasymptotic law of iterated logarithms. We prove that this test is reliable, and adapts to the `signal level,' $\Gamma,$ of any instance, with mean sample costs scaling as $\widetilde{O}(d^2/\Gamma^2)$. We complement this by a minimax lower bound of $\Omega(d/\Gamma^2)$ for sample costs of reliable tests, dominating prior asymptotic lower bounds by capturing the dependence on $d$, and thus elucidating a basic insight missing in the extant literature on such problems.

When are Bandits Robust to Misspecification?

Parametric feature-based reward models are widely employed by algorithms for decision making settings such as bandits and contextual bandits. The typical assumption under which they are analysed is realizability, i.e., that the true rewards of actions are perfectly explained by some parametric model in the class. We are, however, interested in the situation where the true rewards are (potentially significantly) misspecified with respect to the model class. For parameterized bandits and contextual bandits, we identify sufficient conditions, depending on the problem instance and model class, under which classic algorithms such as $\epsilon$-greedy and LinUCB enjoy sublinear (in the time horizon) regret guarantees under even grossly misspecified rewards. This is in contrast to existing worst-case results for misspecified bandits which show regret bounds that scale linearly with time, and shows that there can be a nontrivially large set of bandit instances that are robust to misspecification.

A Unified Framework for Discovering Discrete Symmetries

We consider the problem of learning a function respecting a symmetry from among a class of symmetries. We develop a unified framework that enables symmetry discovery across a broad range of subgroups including locally symmetric, dihedral and cyclic subgroups. At the core of the framework is a novel architecture composed of linear and tensor-valued functions that expresses functions invariant to these subgroups in a principled manner. The structure of the architecture enables us to leverage multi-armed bandit algorithms and gradient descent to efficiently optimize over the linear and the tensor-valued functions, respectively, and to infer the symmetry that is ultimately learnt. We also discuss the necessity of the tensor-valued functions in the architecture. Experiments on image-digit sum and polynomial regression tasks demonstrate the effectiveness of our approach.

On the Minimax Regret for Linear Bandits in a wide variety of Action Spaces

As noted in the works of \cite{lattimore2020bandit}, it has been mentioned that it is an open problem to characterize the minimax regret of linear bandits in a wide variety of action spaces. In this article we present an optimal regret lower bound for a wide class of convex action spaces.

Exploration in Linear Bandits with Rich Action Sets and its Implications for Inference

We present a non-asymptotic lower bound on the eigenspectrum of the design matrix generated by any linear bandit algorithm with sub-linear regret when the action set has well-behaved curvature. Specifically, we show that the minimum eigenvalue of the expected design matrix grows as $\Omega(\sqrt{n})$ whenever the expected cumulative regret of the algorithm is $O(\sqrt{n})$, where $n$ is the learning horizon, and the action-space has a constant Hessian around the optimal arm. This shows that such action-spaces force a polynomial lower bound rather than a logarithmic lower bound, as shown by \cite{lattimore2017end}, in discrete (i.e., well-separated) action spaces. Furthermore, while the previous result is shown to hold only in the asymptotic regime (as $n \to \infty$), our result for these ``locally rich" action spaces is any-time. Additionally, under a mild technical assumption, we obtain a similar lower bound on the minimum eigen value holding with high probability. We apply our result to two practical scenarios -- \emph{model selection} and \emph{clustering} in linear bandits. For model selection, we show that an epoch-based linear bandit algorithm adapts to the true model complexity at a rate exponential in the number of epochs, by virtue of our novel spectral bound. For clustering, we consider a multi agent framework where we show, by leveraging the spectral result, that no forced exploration is necessary -- the agents can run a linear bandit algorithm and estimate their underlying parameters at once, and hence incur a low regret.

Actor-Critic based Improper Reinforcement Learning

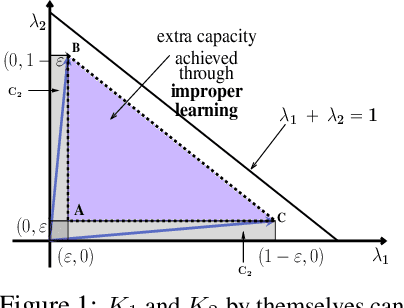
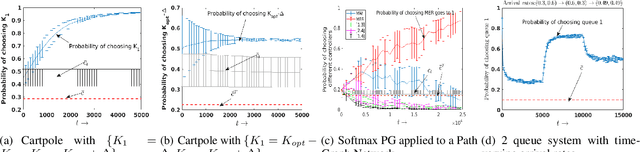
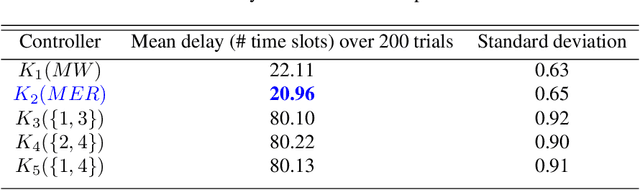
We consider an improper reinforcement learning setting where a learner is given $M$ base controllers for an unknown Markov decision process, and wishes to combine them optimally to produce a potentially new controller that can outperform each of the base ones. This can be useful in tuning across controllers, learnt possibly in mismatched or simulated environments, to obtain a good controller for a given target environment with relatively few trials. Towards this, we propose two algorithms: (1) a Policy Gradient-based approach; and (2) an algorithm that can switch between a simple Actor-Critic (AC) based scheme and a Natural Actor-Critic (NAC) scheme depending on the available information. Both algorithms operate over a class of improper mixtures of the given controllers. For the first case, we derive convergence rate guarantees assuming access to a gradient oracle. For the AC-based approach we provide convergence rate guarantees to a stationary point in the basic AC case and to a global optimum in the NAC case. Numerical results on (i) the standard control theoretic benchmark of stabilizing an cartpole; and (ii) a constrained queueing task show that our improper policy optimization algorithm can stabilize the system even when the base policies at its disposal are unstable.