Label Noise: Ignorance Is Bliss

We establish a new theoretical framework for learning under multi-class, instance-dependent label noise. This framework casts learning with label noise as a form of domain adaptation, in particular, domain adaptation under posterior drift. We introduce the concept of \emph{relative signal strength} (RSS), a pointwise measure that quantifies the transferability from noisy to clean posterior. Using RSS, we establish nearly matching upper and lower bounds on the excess risk. Our theoretical findings support the simple \emph{Noise Ignorant Empirical Risk Minimization (NI-ERM)} principle, which minimizes empirical risk while ignoring label noise. Finally, we translate this theoretical insight into practice: by using NI-ERM to fit a linear classifier on top of a self-supervised feature extractor, we achieve state-of-the-art performance on the CIFAR-N data challenge.

Testing the Feasibility of Linear Programs with Bandit Feedback

While the recent literature has seen a surge in the study of constrained bandit problems, all existing methods for these begin by assuming the feasibility of the underlying problem. We initiate the study of testing such feasibility assumptions, and in particular address the problem in the linear bandit setting, thus characterising the costs of feasibility testing for an unknown linear program using bandit feedback. Concretely, we test if $\exists x: Ax \ge 0$ for an unknown $A \in \mathbb{R}^{m \times d}$, by playing a sequence of actions $x_t\in \mathbb{R}^d$, and observing $Ax_t + \mathrm{noise}$ in response. By identifying the hypothesis as determining the sign of the value of a minimax game, we construct a novel test based on low-regret algorithms and a nonasymptotic law of iterated logarithms. We prove that this test is reliable, and adapts to the `signal level,' $\Gamma,$ of any instance, with mean sample costs scaling as $\widetilde{O}(d^2/\Gamma^2)$. We complement this by a minimax lower bound of $\Omega(d/\Gamma^2)$ for sample costs of reliable tests, dominating prior asymptotic lower bounds by capturing the dependence on $d$, and thus elucidating a basic insight missing in the extant literature on such problems.

Joint Optimization of Piecewise Linear Ensembles

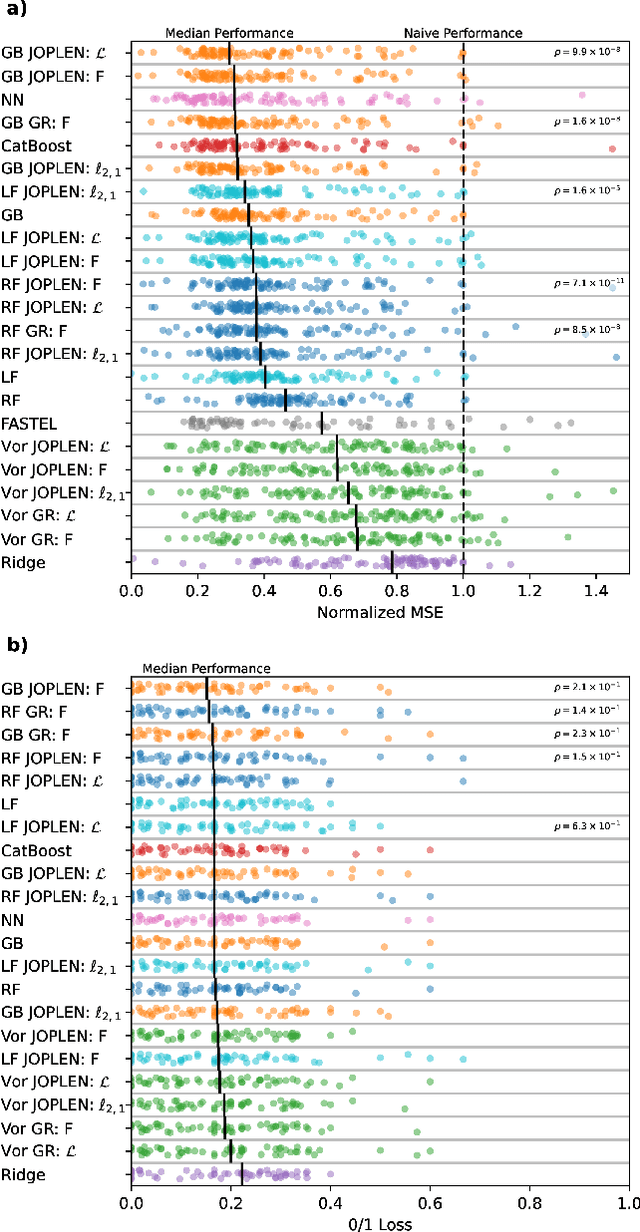
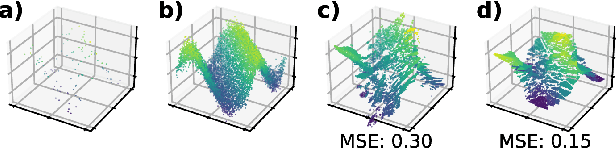
Tree ensembles achieve state-of-the-art performance despite being greedily optimized. Global refinement (GR) reduces greediness by jointly and globally optimizing all constant leaves. We propose Joint Optimization of Piecewise Linear ENsembles (JOPLEN), a piecewise-linear extension of GR. Compared to GR, JOPLEN improves model flexibility and can apply common penalties, including sparsity-promoting matrix norms and subspace-norms, to nonlinear prediction. We evaluate the Frobenius norm, $\ell_{2,1}$ norm, and Laplacian regularization for 146 regression and classification datasets; JOPLEN, combined with GB trees and RF, achieves superior performance in both settings. Additionally, JOPLEN with a nuclear norm penalty empirically learns smooth and subspace-aligned functions. Finally, we perform multitask feature selection by extending the Dirty LASSO. JOPLEN Dirty LASSO achieves a superior feature sparsity/performance tradeoff to linear and gradient boosted approaches. We anticipate that JOPLEN will improve regression, classification, and feature selection across many fields.

Universal Feature Selection for Simultaneous Interpretability of Multitask Datasets

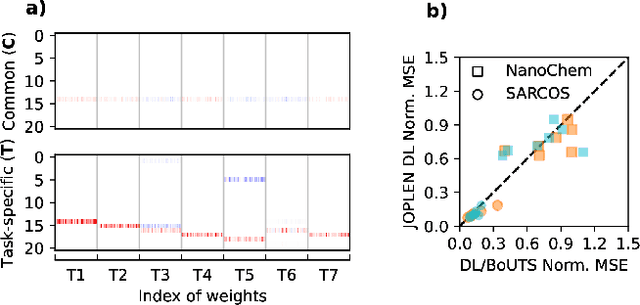
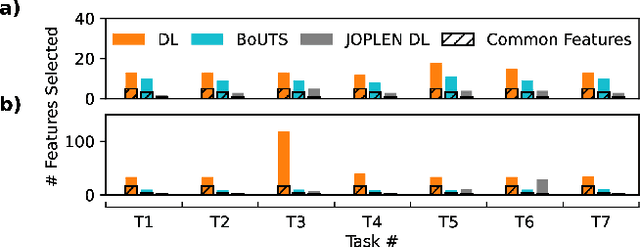
Extracting meaningful features from complex, high-dimensional datasets across scientific domains remains challenging. Current methods often struggle with scalability, limiting their applicability to large datasets, or make restrictive assumptions about feature-property relationships, hindering their ability to capture complex interactions. BoUTS's general and scalable feature selection algorithm surpasses these limitations to identify both universal features relevant to all datasets and task-specific features predictive for specific subsets. Evaluated on seven diverse chemical regression datasets, BoUTS achieves state-of-the-art feature sparsity while maintaining prediction accuracy comparable to specialized methods. Notably, BoUTS's universal features enable domain-specific knowledge transfer between datasets, and suggest deep connections in seemingly-disparate chemical datasets. We expect these results to have important repercussions in manually-guided inverse problems. Beyond its current application, BoUTS holds immense potential for elucidating data-poor systems by leveraging information from similar data-rich systems. BoUTS represents a significant leap in cross-domain feature selection, potentially leading to advancements in various scientific fields.

Unified Binary and Multiclass Margin-Based Classification

The notion of margin loss has been central to the development and analysis of algorithms for binary classification. To date, however, there remains no consensus as to the analogue of the margin loss for multiclass classification. In this work, we show that a broad range of multiclass loss functions, including many popular ones, can be expressed in the relative margin form, a generalization of the margin form of binary losses. The relative margin form is broadly useful for understanding and analyzing multiclass losses as shown by our prior work (Wang and Scott, 2020, 2021). To further demonstrate the utility of this way of expressing multiclass losses, we use it to extend the seminal result of Bartlett et al. (2006) on classification-calibration of binary margin losses to multiclass. We then analyze the class of Fenchel-Young losses, and expand the set of these losses that are known to be classification-calibrated.

Fusing Sparsity with Deep Learning for Rotating Scatter Mask Gamma Imaging

Many nuclear safety applications need fast, portable, and accurate imagers to better locate radiation sources. The Rotating Scatter Mask (RSM) system is an emerging device with the potential to meet these needs. The main challenge is the under-determined nature of the data acquisition process: the dimension of the measured signal is far less than the dimension of the image to be reconstructed. To address this challenge, this work aims to fuse model-based sparsity-promoting regularization and a data-driven deep neural network denoising image prior to perform image reconstruction. An efficient algorithm is developed and produces superior reconstructions relative to current approaches.

Mixture Proportion Estimation Beyond Irreducibility

The task of mixture proportion estimation (MPE) is to estimate the weight of a component distribution in a mixture, given observations from both the component and mixture. Previous work on MPE adopts the irreducibility assumption, which ensures identifiablity of the mixture proportion. In this paper, we propose a more general sufficient condition that accommodates several settings of interest where irreducibility does not hold. We further present a resampling-based meta-algorithm that takes any existing MPE algorithm designed to work under irreducibility and adapts it to work under our more general condition. Our approach empirically exhibits improved estimation performance relative to baseline methods and to a recently proposed regrouping-based algorithm.

Label Embedding by Johnson-Lindenstrauss Matrices

We present a simple and scalable framework for extreme multiclass classification based on Johnson-Lindenstrauss matrices (JLMs). Using the columns of a JLM to embed the labels, a $C$-class classification problem is transformed into a regression problem with $\cO(\log C)$ output dimension. We derive an excess risk bound, revealing a tradeoff between computational efficiency and prediction accuracy, and further show that under the Massart noise condition, the penalty for dimension reduction vanishes. Our approach is easily parallelizable, and experimental results demonstrate its effectiveness and scalability in large-scale applications.

Learning from Label Proportions by Learning with Label Noise

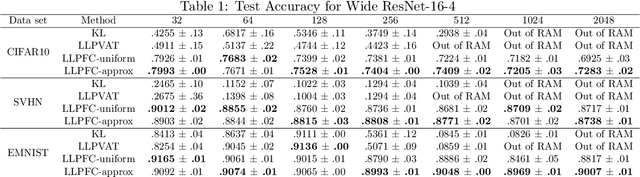
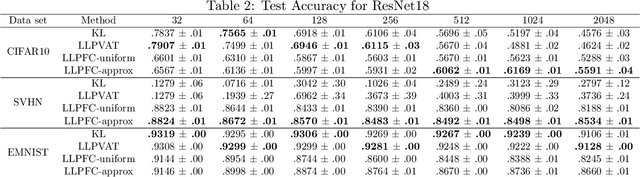
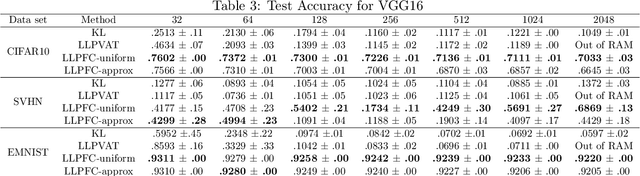
Learning from label proportions (LLP) is a weakly supervised classification problem where data points are grouped into bags, and the label proportions within each bag are observed instead of the instance-level labels. The task is to learn a classifier to predict the individual labels of future individual instances. Prior work on LLP for multi-class data has yet to develop a theoretically grounded algorithm. In this work, we provide a theoretically grounded approach to LLP based on a reduction to learning with label noise, using the forward correction (FC) loss of \citet{Patrini2017MakingDN}. We establish an excess risk bound and generalization error analysis for our approach, while also extending the theory of the FC loss which may be of independent interest. Our approach demonstrates improved empirical performance in deep learning scenarios across multiple datasets and architectures, compared to the leading existing methods.

Supervised PCA: A Multiobjective Approach

Methods for supervised principal component analysis (SPCA) aim to incorporate label information into principal component analysis (PCA), so that the extracted features are more useful for a prediction task of interest. Prior work on SPCA has focused primarily on optimizing prediction error, and has neglected the value of maximizing variance explained by the extracted features. We propose a new method for SPCA that addresses both of these objectives jointly, and demonstrate empirically that our approach dominates existing approaches, i.e., outperforms them with respect to both prediction error and variation explained. Our approach accommodates arbitrary supervised learning losses and, through a statistical reformulation, provides a novel low-rank extension of generalized linear models.