E2E-FANet: A Highly Generalizable Framework for Waves prediction Behind Floating Breakwaters via Exogenous-to-Endogenous Variable Attention

Accurate prediction of waves behind floating breakwaters (FB) is crucial for optimizing coastal engineering structures, enhancing safety, and improving design efficiency. Existing methods demonstrate limitations in capturing nonlinear interactions between waves and structures, while exhibiting insufficient capability in modeling the complex frequency-domain relationships among elevations of different wave gauges. To address these challenges, this study introduces the Exogenous-to-Endogenous Frequency-Aware Network (E2E-FANet), a novel end-to-end neural network designed to model relationships between waves and structures. The E2E-FANetarchitecture incorporates a Dual-Basis Frequency Mapping (DBFM) module that leverages orthogonal cosine and sine bases to extract wave features from the frequency domain while preserving temporal information. Additionally, we introduce the Exogenous-to-Endogenous Cross-Attention (E2ECA) module, which employs cross attention to model the interactions between endogenous and exogenous variables. We incorporate a Temporal-wise Attention (TA) mechanism that adaptively captures complex dependencies in endogenous variables. These integrated modules function synergistically, enabling E2E-FANet to achieve both comprehensive feature perception in the time-frequency domain and precise modeling of wave-structure interactions. To comprehensively evaluate the performance of E2E-FANet, we constructed a multi-level validation framework comprising three distinct testing scenarios: internal validation under identical wave conditions, generalization testing across different wave conditions, and adaptability testing with varying relative water density (RW) conditions. These comprehensive tests demonstrate that E2E-FANet provides accurate waves behind FB predictions while successfully generalizing diverse wave conditions.

A Novel Framework for Significant Wave Height Prediction based on Adaptive Feature Extraction Time-Frequency Network

Precise forecasting of significant wave height (Hs) is essential for the development and utilization of wave energy. The challenges in predicting Hs arise from its non-linear and non-stationary characteristics. The combination of decomposition preprocessing and machine learning models have demonstrated significant effectiveness in Hs prediction by extracting data features. However, decomposing the unknown data in the test set can lead to data leakage issues. To simultaneously achieve data feature extraction and prevent data leakage, a novel Adaptive Feature Extraction Time-Frequency Network (AFE-TFNet) is proposed to improve prediction accuracy and stability. It is encoder-decoder rolling framework. The encoder consists of two stages: feature extraction and feature fusion. In the feature extraction stage, global and local frequency domain features are extracted by combining Wavelet Transform (WT) and Fourier Transform (FT), and multi-scale frequency analysis is performed using Inception blocks. In the feature fusion stage, time-domain and frequency-domain features are integrated through dominant harmonic sequence energy weighting (DHSEW). The decoder employed an advanced long short-term memory (LSTM) model. Hourly measured wind speed (Ws), dominant wave period (DPD), average wave period (APD) and Hs from three stations are used as the dataset, and the four metrics are employed to evaluate the forecasting performance. Results show that AFE-TFNet significantly outperforms benchmark methods in terms of prediction accuracy. Feature extraction can significantly improve the prediction accuracy. DHSEW has substantially increased the accuracy of medium-term to long-term forecasting. The prediction accuracy of AFE-TFNet does not demonstrate significant variability with changes of rolling time window size. Overall, AFE-TFNet shows strong potential for handling complex signal forecasting.

Label Noise: Ignorance Is Bliss

We establish a new theoretical framework for learning under multi-class, instance-dependent label noise. This framework casts learning with label noise as a form of domain adaptation, in particular, domain adaptation under posterior drift. We introduce the concept of \emph{relative signal strength} (RSS), a pointwise measure that quantifies the transferability from noisy to clean posterior. Using RSS, we establish nearly matching upper and lower bounds on the excess risk. Our theoretical findings support the simple \emph{Noise Ignorant Empirical Risk Minimization (NI-ERM)} principle, which minimizes empirical risk while ignoring label noise. Finally, we translate this theoretical insight into practice: by using NI-ERM to fit a linear classifier on top of a self-supervised feature extractor, we achieve state-of-the-art performance on the CIFAR-N data challenge.

Efficient Training of Neural Stochastic Differential Equations by Matching Finite Dimensional Distributions

Neural Stochastic Differential Equations (Neural SDEs) have emerged as powerful mesh-free generative models for continuous stochastic processes, with critical applications in fields such as finance, physics, and biology. Previous state-of-the-art methods have relied on adversarial training, such as GANs, or on minimizing distance measures between processes using signature kernels. However, GANs suffer from issues like instability, mode collapse, and the need for specialized training techniques, while signature kernel-based methods require solving linear PDEs and backpropagating gradients through the solver, whose computational complexity scales quadratically with the discretization steps. In this paper, we identify a novel class of strictly proper scoring rules for comparing continuous Markov processes. This theoretical finding naturally leads to a novel approach called Finite Dimensional Matching (FDM) for training Neural SDEs. Our method leverages the Markov property of SDEs to provide a computationally efficient training objective. This scoring rule allows us to bypass the computational overhead associated with signature kernels and reduces the training complexity from $O(D^2)$ to $O(D)$ per epoch, where $D$ represents the number of discretization steps of the process. We demonstrate that FDM achieves superior performance, consistently outperforming existing methods in terms of both computational efficiency and generative quality.

PM2: A New Prompting Multi-modal Model Paradigm for Few-shot Medical Image Classification

Few-shot learning has been successfully applied to medical image classification as only very few medical examples are available for training. Due to the challenging problem of limited number of annotated medical images, image representations should not be solely derived from a single image modality which is insufficient for characterizing concept classes. In this paper, we propose a new prompting multi-modal model paradigm on medical image classification based on multi-modal foundation models, called PM2. Besides image modality,PM2 introduces another supplementary text input, known as prompt, to further describe corresponding image or concept classes and facilitate few-shot learning across diverse modalities. To better explore the potential of prompt engineering, we empirically investigate five distinct prompt schemes under the new paradigm. Furthermore, linear probing in multi-modal models acts as a linear classification head taking as input only class token, which ignores completely merits of rich statistics inherent in high-level visual tokens. Thus, we alternatively perform a linear classification on feature distribution of visual tokens and class token simultaneously. To effectively mine such rich statistics, a global covariance pooling with efficient matrix power normalization is used to aggregate visual tokens. Then we study and combine two classification heads. One is shared for class token of image from vision encoder and prompt representation encoded by text encoder. The other is to classification on feature distribution of visual tokens from vision encoder. Extensive experiments on three medical datasets show that our PM2 significantly outperforms counterparts regardless of prompt schemes and achieves state-of-the-art performance.

Label Embedding by Johnson-Lindenstrauss Matrices

We present a simple and scalable framework for extreme multiclass classification based on Johnson-Lindenstrauss matrices (JLMs). Using the columns of a JLM to embed the labels, a $C$-class classification problem is transformed into a regression problem with $\cO(\log C)$ output dimension. We derive an excess risk bound, revealing a tradeoff between computational efficiency and prediction accuracy, and further show that under the Massart noise condition, the penalty for dimension reduction vanishes. Our approach is easily parallelizable, and experimental results demonstrate its effectiveness and scalability in large-scale applications.

Learning from Label Proportions by Learning with Label Noise

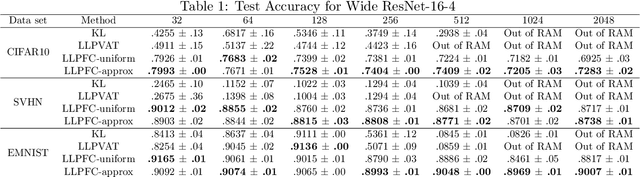
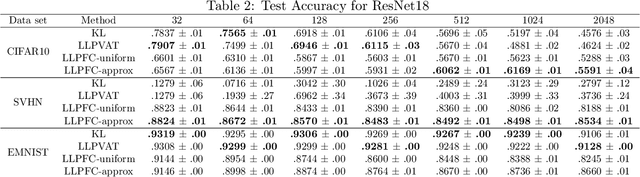
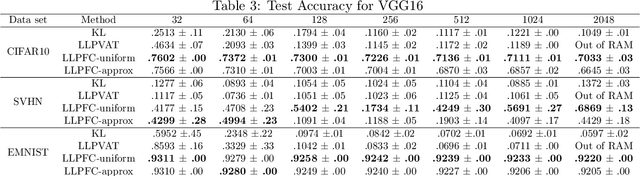
Learning from label proportions (LLP) is a weakly supervised classification problem where data points are grouped into bags, and the label proportions within each bag are observed instead of the instance-level labels. The task is to learn a classifier to predict the individual labels of future individual instances. Prior work on LLP for multi-class data has yet to develop a theoretically grounded algorithm. In this work, we provide a theoretically grounded approach to LLP based on a reduction to learning with label noise, using the forward correction (FC) loss of \citet{Patrini2017MakingDN}. We establish an excess risk bound and generalization error analysis for our approach, while also extending the theory of the FC loss which may be of independent interest. Our approach demonstrates improved empirical performance in deep learning scenarios across multiple datasets and architectures, compared to the leading existing methods.

Learning from Label Proportions: A Mutual Contamination Framework

Learning from label proportions (LLP) is a weakly supervised setting for classification in which unlabeled training instances are grouped into bags, and each bag is annotated with the proportion of each class occurring in that bag. Prior work on LLP has yet to establish a consistent learning procedure, nor does there exist a theoretically justified, general purpose training criterion. In this work we address these two issues by posing LLP in terms of mutual contamination models (MCMs), which have recently been applied successfully to study various other weak supervision settings. In the process, we establish several novel technical results for MCMs, including unbiased losses and generalization error bounds under non-iid sampling plans. We also point out the limitations of a common experimental setting for LLP, and propose a new one based on our MCM framework.

Learning from Multiple Corrupted Sources, with Application to Learning from Label Proportions

We study binary classification in the setting where the learner is presented with multiple corrupted training samples, with possibly different sample sizes and degrees of corruption, and introduce an approach based on minimizing a weighted combination of corruption-corrected empirical risks. We establish a generalization error bound, and further show that the bound is optimized when the weights are certain interpretable and intuitive functions of the sample sizes and degrees of corruptions. We then apply this setting to the problem of learning with label proportions (LLP), and propose an algorithm that enjoys the most general statistical performance guarantees known for LLP. Experiments demonstrate the utility of our theory.