Supervised PCA: A Multiobjective Approach
Paper and Code
Nov 10, 2020
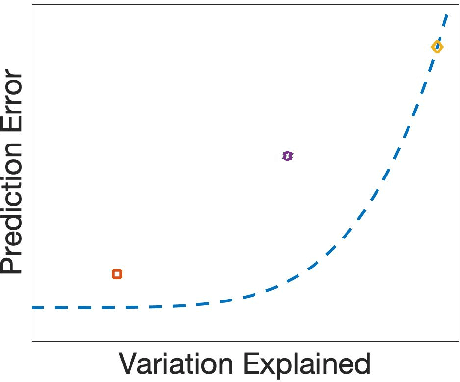
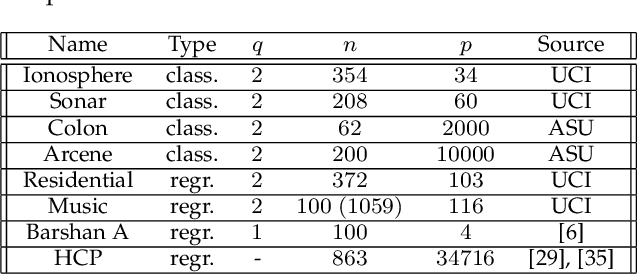
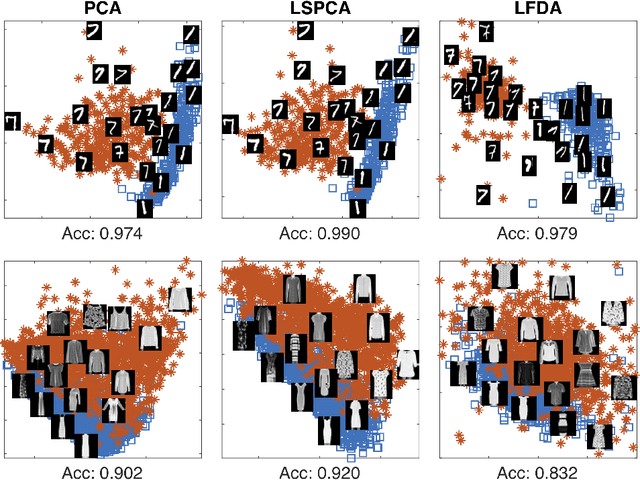
Methods for supervised principal component analysis (SPCA) aim to incorporate label information into principal component analysis (PCA), so that the extracted features are more useful for a prediction task of interest. Prior work on SPCA has focused primarily on optimizing prediction error, and has neglected the value of maximizing variance explained by the extracted features. We propose a new method for SPCA that addresses both of these objectives jointly, and demonstrate empirically that our approach dominates existing approaches, i.e., outperforms them with respect to both prediction error and variation explained. Our approach accommodates arbitrary supervised learning losses and, through a statistical reformulation, provides a novel low-rank extension of generalized linear models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge