Actor-Critic based Improper Reinforcement Learning

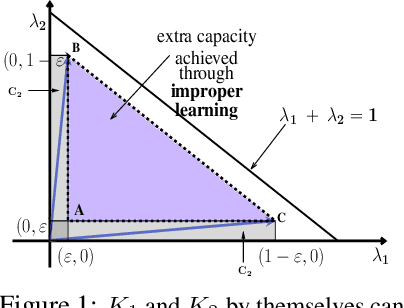
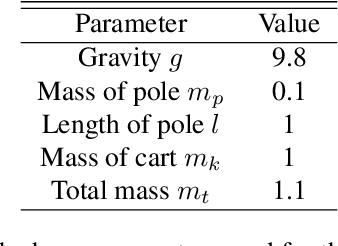
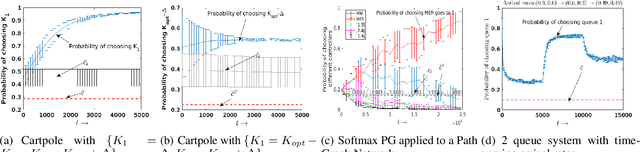
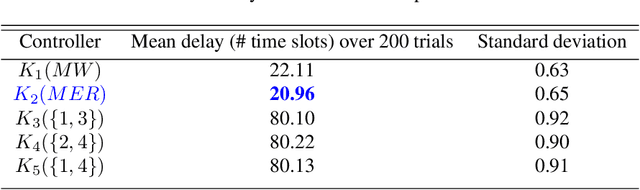
We consider an improper reinforcement learning setting where a learner is given $M$ base controllers for an unknown Markov decision process, and wishes to combine them optimally to produce a potentially new controller that can outperform each of the base ones. This can be useful in tuning across controllers, learnt possibly in mismatched or simulated environments, to obtain a good controller for a given target environment with relatively few trials. Towards this, we propose two algorithms: (1) a Policy Gradient-based approach; and (2) an algorithm that can switch between a simple Actor-Critic (AC) based scheme and a Natural Actor-Critic (NAC) scheme depending on the available information. Both algorithms operate over a class of improper mixtures of the given controllers. For the first case, we derive convergence rate guarantees assuming access to a gradient oracle. For the AC-based approach we provide convergence rate guarantees to a stationary point in the basic AC case and to a global optimum in the NAC case. Numerical results on (i) the standard control theoretic benchmark of stabilizing an cartpole; and (ii) a constrained queueing task show that our improper policy optimization algorithm can stabilize the system even when the base policies at its disposal are unstable.

Decentralized, Hybrid MAC Design with Reduced State Information Exchange for Low-Delay IoT Applications

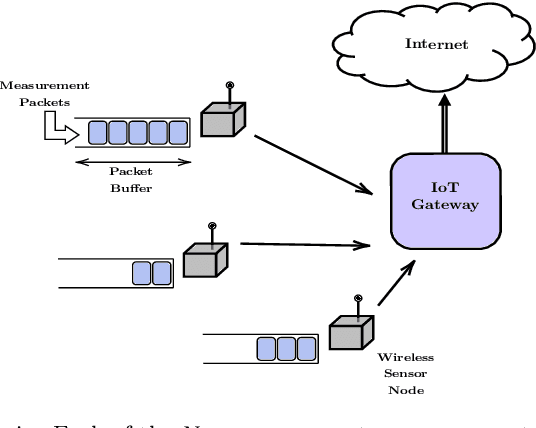
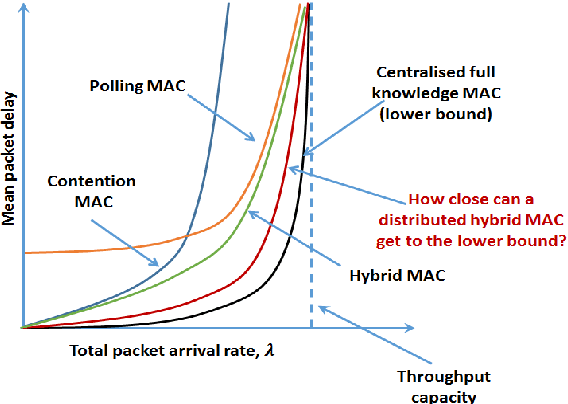
We consider a system of several collocated nodes sharing a time slotted wireless channel, and seek a MAC that (i) provides low mean delay, (ii) has distributed control (i.e., there is no central scheduler), and (iii) does not require explicit exchange of state information or control signals. The design of such MAC protocols must keep in mind the need for contention access at light traffic, and scheduled access in heavy traffic, leading to the long-standing interest in hybrid, adaptive MACs. We first propose EZMAC, a simple extension of an existing decentralized, hybrid MAC called ZMAC. Next, motivated by our results on delay and throughput optimality in partially observed, constrained queuing networks, we develop another decentralized MAC protocol that we term QZMAC. A method to improve the short-term fairness of QZMAC is proposed and analysed, and the resulting modified algorithm is shown to possess better fairness properties than QZMAC. The theory developed to reduce delay is also shown to work %with different traffic types (batch arrivals, for example) and even in the presence of transmission errors and fast fading. Extensions to handle time critical traffic (alarms, for example) and hidden nodes are also discussed. Practical implementation issues, such as handling Clear Channel Assessment (CCA) errors, are outlined. We implement and demonstrate the performance of QZMAC on a test bed consisting of CC2420 based Crossbow telosB motes, running the 6TiSCH communication stack on the Contiki operating system over the 2.4GHz ISM band. Finally, using simulations, we show that both protocols achieve mean delays much lower than those achieved by ZMAC, and QZMAC provides mean delays very close to the minimum achievable in this setting, i.e., that of the centralized complete knowledge scheduler.

Improper Learning with Gradient-based Policy Optimization

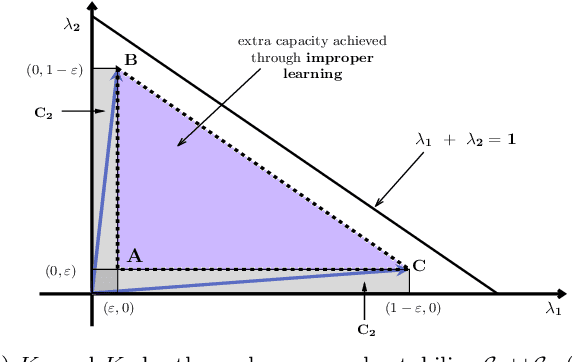
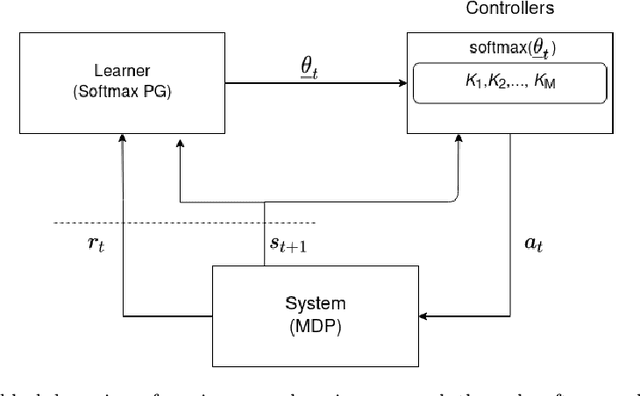
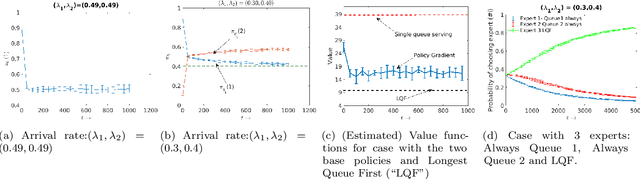
We consider an improper reinforcement learning setting where the learner is given M base controllers for an unknown Markov Decision Process, and wishes to combine them optimally to produce a potentially new controller that can outperform each of the base ones. We propose a gradient-based approach that operates over a class of improper mixtures of the controllers. The value function of the mixture and its gradient may not be available in closed-form; however, we show that we can employ rollouts and simultaneous perturbation stochastic approximation (SPSA) for explicit gradient descent optimization. We derive convergence and convergence rate guarantees for the approach assuming access to a gradient oracle. Numerical results on a challenging constrained queueing task show that our improper policy optimization algorithm can stabilize the system even when each constituent policy at its disposal is unstable.

Towards Optimal and Efficient Best Arm Identification in Linear Bandits

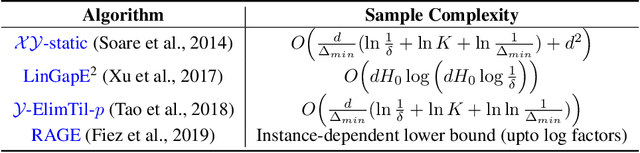
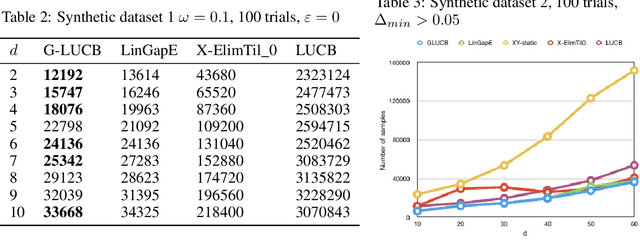
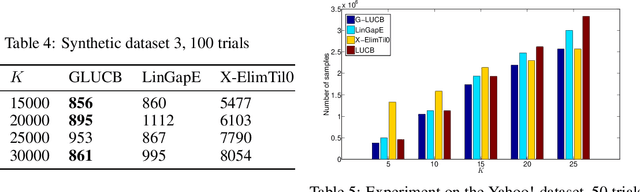
We give a new algorithm for best arm identification in linearly parameterised bandits in the fixed confidence setting. The algorithm generalises the well-known LUCB algorithm of Kalyanakrishnan et al. (2012) by playing an arm which minimises a suitable notion of geometric overlap of the statistical confidence set for the unknown parameter, and is fully adaptive and computationally efficient as compared to several state-of-the methods. We theoretically analyse the sample complexity of the algorithm for problems with two and three arms, showing optimality in many cases. Numerical results indicate favourable performance over other algorithms with which we compare.