Arpan Chattopadhyay
Low-Complexity Super-Resolution Signature Estimation of XL-MIMO FMCW Radar
Jun 09, 2025Abstract:Extremely Large-Scale (XL) multiple input multiple output (MIMO) antenna systems combined with ultra-wide signal bandwidth (BW) offer the potential for ultra-high-resolution sensing in frequency modulated continuous wave (FMCW) radars. However, the use of ultra-wide BW results in significant spatial delays across the array aperture, comparable to the range resolution, leading to the spatial wideband effect (SWE). SWE introduces coupling between the range and angle domains, rendering conventional narrowband signal processing techniques ineffective for target signature estimation. In this paper, we propose an efficient super-resolution signature estimation technique for XL-MIMO FMCW radars operating under SWE, leveraging compressive sensing (CS) methods. The proposed 2D CS-based approach offers low computational complexity, making it highly suitable for real-time applications in large-scale radar systems. Numerical simulation results validate the superior performance of the proposed method compared to existing wideband and narrowband estimation techniques.
Quickest change detection for UAV-based sensing
Apr 10, 2025



Abstract:This paper addresses the problem of quickest change detection (QCD) at two spatially separated locations monitored by a single unmanned aerial vehicle (UAV) equipped with a sensor. At any location, the UAV observes i.i.d. data sequentially in discrete time instants. The distribution of the observation data changes at some unknown, arbitrary time and the UAV has to detect this change in the shortest possible time. Change can occur at most at one location over the entire infinite time horizon. The UAV switches between these two locations in order to quickly detect the change. To this end, we propose Location Switching and Change Detection (LS-CD) algorithm which uses a repeated one-sided sequential probability ratio test (SPRT) based mechanism for observation-driven location switching and change detection. The primary goal is to minimize the worst-case average detection delay (WADD) while meeting constraints on the average run length to false alarm (ARL2FA) and the UAV's time-averaged energy consumption. We provide a rigorous theoretical analysis of the algorithm's performance by using theory of random walk. Specifically, we derive tight upper and lower bounds to its ARL2FA and a tight upper bound to its WADD. In the special case of a symmetrical setting, our analysis leads to a new asymptotic upper bound to the ARL2FA of the standard CUSUM algorithm, a novel contribution not available in the literature, to our knowledge. Numerical simulations demonstrate the efficacy of LS-CD.
Minimizing Age of Detection for a Markov Source over a Lossy Channel
Mar 04, 2025Abstract:Monitoring a process/phenomenon of specific interest is prevalent in Cyber-Physical Systems (CPS), remote healthcare, smart buildings, intelligent transport, industry 4.0, etc. A key building block of the monitoring system is a sensor sampling the process and communicating the status updates to a monitor for detecting events of interest. Measuring the freshness of the status updates is essential for the timely detection of events, and it has received significant research interest in recent times. In this paper, we propose a new freshness metric, Age of Detection (AoD), for monitoring the state transitions of a Discrete Time Markov Chain (DTMC) source over a lossy wireless channel. We consider the pull model where the sensor samples DTMC state whenever the monitor requests a status update. We formulate a Constrained Markov Decision Problem (CMDP) for optimising the AoD subject to a constraint on the average sampling frequency and solve it using the Lagrangian MDP formulation and Relative Value Iteration (RVI) algorithm. Our numerical results show interesting trade-offs between AoD, sampling frequency, and transmission success probability. Further, the AoD minimizing policy provides a lower estimation error than the Age of Information (AoI) minimizing policy, thus demonstrating the utility of AoD for monitoring DTMC sources.
Multi-target Range, Doppler and Angle estimation in MIMO-FMCW Radar with Limited Measurements
Feb 03, 2025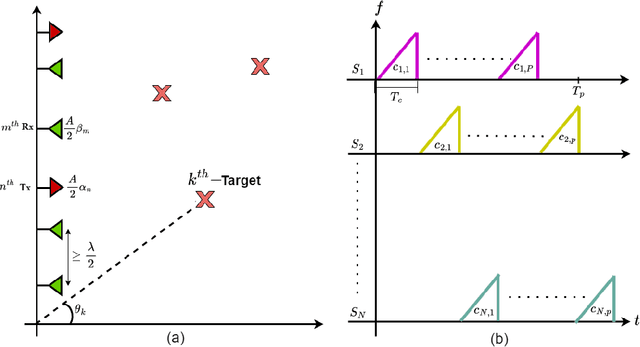
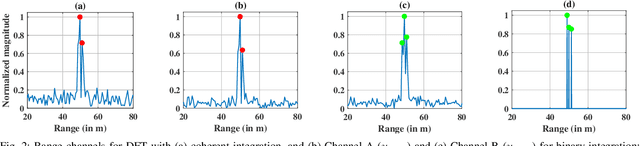
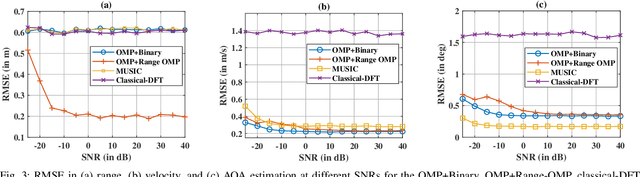
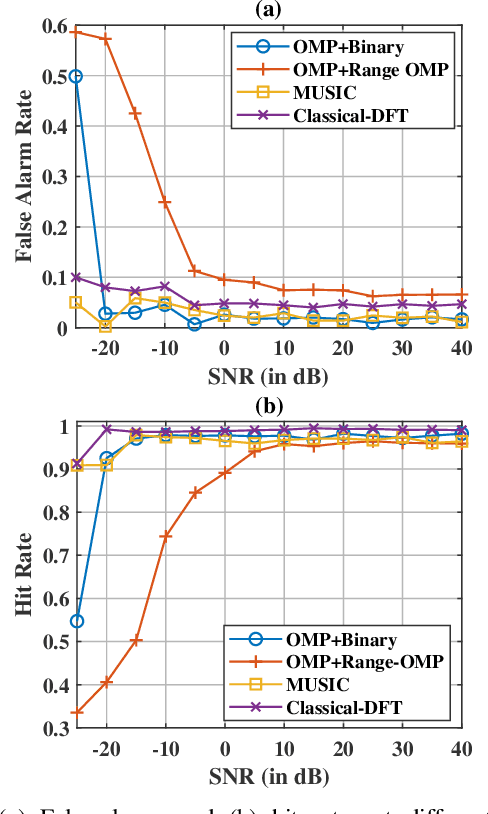
Abstract:Multiple-input multiple-output (MIMO) radar offers several performance and flexibility advantages over traditional radar arrays. However, high angular and Doppler resolutions necessitate a large number of antenna elements and the transmission of numerous chirps, leading to increased hardware and computational complexity. While compressive sensing (CS) has recently been applied to pulsed-waveform radars with sparse measurements, its application to frequency-modulated continuous wave (FMCW) radar for target detection remains largely unexplored. In this paper, we propose a novel CS-based multi-target localization algorithm in the range, Doppler, and angular domains for MIMO-FMCW radar, where we jointly estimate targets' velocities and angles of arrival. To this end, we present a signal model for sparse-random and uniform linear arrays based on three-dimensional spectral estimation. For range estimation, we propose a discrete Fourier transform (DFT)-based focusing and orthogonal matching pursuit (OMP)-based techniques, each with distinct advantages, while two-dimensional CS is used for joint Doppler-angle estimation. Leveraging the properties of structured random matrices, we establish theoretical uniform and non-uniform recovery guarantees with high probability for the proposed framework. Our numerical experiments demonstrate that our methods achieve similar detection performance and higher resolution compared to conventional DFT and MUSIC with fewer transmitted chirps and antenna elements.
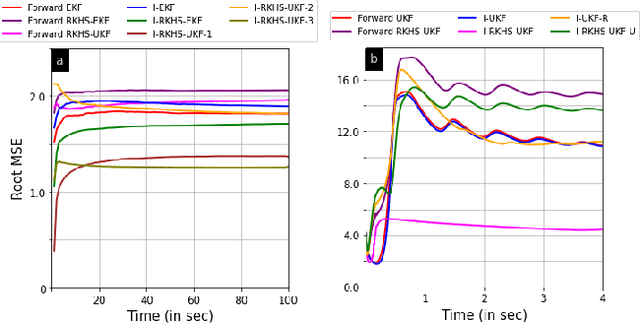
Inverse Particle and Ensemble Kalman Filters
Jul 23, 2024Abstract:In cognitive systems, recent emphasis has been placed on studying cognitive processes of the subject whose behavior was the primary focus of the system's cognitive response. This approach, known as inverse cognition, arises in counter-adversarial applications and has motivated the development of inverse Bayesian filters. In this context, a cognitive adversary, such as a radar, uses a forward Bayesian filter to track its target of interest. An inverse filter is then employed to infer adversary's estimate of target's or defender's state. Previous studies have addressed this inverse filtering problem by introducing methods like inverse Kalman filter (I-KF), inverse extended KF (I-EKF), and inverse unscented KF (I-UKF). However, these inverse filters assume additive Gaussian noises and/or rely on local approximations of non-linear dynamics at the state estimates, limiting their practical application. Contrarily, this paper adopts a global filtering approach and develops an inverse particle filter (I-PF). The particle filter framework employs Monte Carlo (MC) methods to approximate arbitrary posterior distributions. Moreover, under mild system-level conditions, the proposed I-PF demonstrates convergence to the optimal inverse filter. Additionally, we explore MC techniques to approximate Gaussian posteriors and introduce inverse Gaussian PF (I-GPF) and inverse ensemble KF (I-EnKF). Our I-GPF and I-EnKF can efficiently handle non-Gaussian noises with suitable modifications. Additionally, we propose the differentiable I-PF, differentiable I-EnKF, and reproducing kernel Hilbert space-based EnKF (RKHS-EnKF) methods to address scenarios where system information is unknown to defender. Using recursive Cram\'er-Rao lower bound and non-credibility index (NCI), our numerical experiments for different applications demonstrate the estimation performance and time complexity of the proposed filters.
Quickest Detection of False Data Injection Attack in Distributed Process Tracking
Feb 15, 2024Abstract:This paper addresses the problem of detecting false data injection (FDI) attacks in a distributed network without a fusion center, represented by a connected graph among multiple agent nodes. Each agent node is equipped with a sensor, and uses a Kalman consensus information filter (KCIF) to track a discrete time global process with linear dynamics and additive Gaussian noise. The state estimate of the global process at any sensor is computed from the local observation history and the information received by that agent node from its neighbors. At an unknown time, an attacker starts altering the local observation of one agent node. In the Bayesian setting where there is a known prior distribution of the attack beginning instant, we formulate a Bayesian quickest change detection (QCD) problem for FDI detection in order to minimize the mean detection delay subject to a false alarm probability constraint. While it is well-known that the optimal Bayesian QCD rule involves checking the Shriyaev's statistic against a threshold, we demonstrate how to compute the Shriyaev's statistic at each node in a recursive fashion given our non-i.i.d. observations. Next, we consider non-Bayesian QCD where the attack begins at an arbitrary and unknown time, and the detector seeks to minimize the worst case detection delay subject to a constraint on the mean time to false alarm and probability of misidentification. We use the multiple hypothesis sequential probability ratio test for attack detection and identification at each sensor. For unknown attack strategy, we use the window-limited generalized likelihood ratio (WL-GLR) algorithm to solve the QCD problem. Numerical results demonstrate the performances and trade-offs of the proposed algorithms.
Inverse Reinforcement Learning With Constraint Recovery
May 14, 2023Abstract:In this work, we propose a novel inverse reinforcement learning (IRL) algorithm for constrained Markov decision process (CMDP) problems. In standard IRL problems, the inverse learner or agent seeks to recover the reward function of the MDP, given a set of trajectory demonstrations for the optimal policy. In this work, we seek to infer not only the reward functions of the CMDP, but also the constraints. Using the principle of maximum entropy, we show that the IRL with constraint recovery (IRL-CR) problem can be cast as a constrained non-convex optimization problem. We reduce it to an alternating constrained optimization problem whose sub-problems are convex. We use exponentiated gradient descent algorithm to solve it. Finally, we demonstrate the efficacy of our algorithm for the grid world environment.
Inverse Unscented Kalman Filter
Apr 04, 2023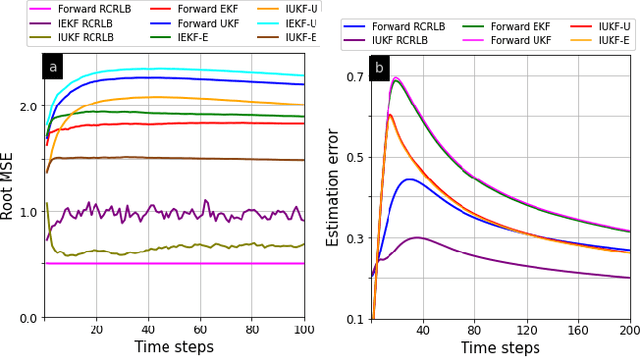
Abstract:Rapid advances in designing cognitive and counter-adversarial systems have motivated the development of inverse Bayesian filters. In this setting, a cognitive `adversary' tracks its target of interest via a stochastic framework such as a Kalman filter (KF). The target or `defender' then employs another inverse stochastic filter to infer the forward filter estimates of the defender computed by the adversary. For linear systems, inverse Kalman filter (I-KF) has been recently shown to be effective in these counter-adversarial applications. In the paper, contrary to prior works, we focus on non-linear system dynamics and formulate the inverse unscented KF (I-UKF) to estimate the defender's state with reduced linearization errors. We then generalize this framework to an unknown system model by proposing reproducing kernel Hilbert space-based UKF (RKHS-UKF) to learn the system dynamics and estimate the state based on its observations. Our theoretical analyses to guarantee the stochastic stability of I-UKF and RKHS-UKF in the mean-squared sense shows that, provided the forward filters are stable, the inverse filters are also stable under mild system-level conditions. Our numerical experiments for several different applications demonstrate the state estimation performance of the proposed filters using recursive Cram\'{e}r-Rao lower bound as a benchmark.
Inverse Cubature and Quadrature Kalman filters
Mar 18, 2023Abstract:Recent developments in counter-adversarial system research have led to the development of inverse stochastic filters that are employed by a defender to infer the information its adversary may have learned. Prior works addressed this inverse cognition problem by proposing inverse Kalman filter (I-KF) and inverse extended KF (I-EKF), respectively, for linear and non-linear Gaussian state-space models. However, in practice, many counter-adversarial settings involve highly non-linear system models, wherein EKF's linearization often fails. In this paper, we consider the efficient numerical integration techniques to address such nonlinearities and, to this end, develop inverse cubature KF (I-CKF) and inverse quadrature KF (I-QKF). We derive the stochastic stability conditions for the proposed filters in the exponential-mean-squared-boundedness sense. Numerical experiments demonstrate the estimation accuracy of our I-CKF and I-QKF with the recursive Cram\'{e}r-Rao lower bound as a benchmark.
Online Reinforcement Learning in Periodic MDP
Mar 16, 2023Abstract:We study learning in periodic Markov Decision Process (MDP), a special type of non-stationary MDP where both the state transition probabilities and reward functions vary periodically, under the average reward maximization setting. We formulate the problem as a stationary MDP by augmenting the state space with the period index, and propose a periodic upper confidence bound reinforcement learning-2 (PUCRL2) algorithm. We show that the regret of PUCRL2 varies linearly with the period $N$ and as $\mathcal{O}(\sqrt{Tlog T})$ with the horizon length $T$. Utilizing the information about the sparsity of transition matrix of augmented MDP, we propose another algorithm PUCRLB which enhances upon PUCRL2, both in terms of regret ($O(\sqrt{N})$ dependency on period) and empirical performance. Finally, we propose two other algorithms U-PUCRL2 and U-PUCRLB for extended uncertainty in the environment in which the period is unknown but a set of candidate periods are known. Numerical results demonstrate the efficacy of all the algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge