Multi-target Range, Doppler and Angle estimation in MIMO-FMCW Radar with Limited Measurements

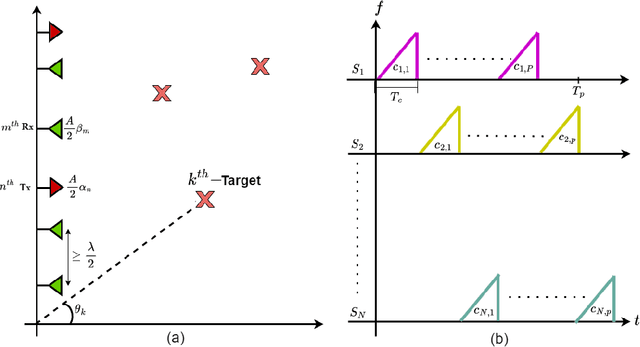
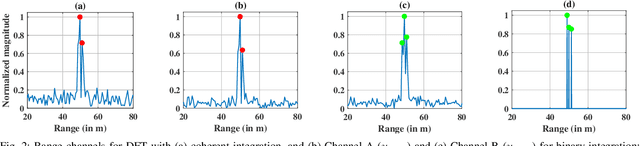
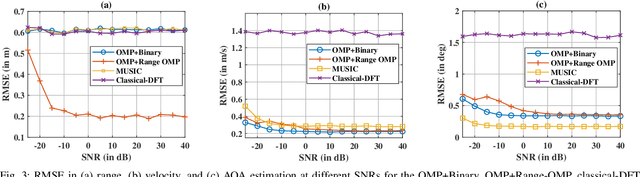
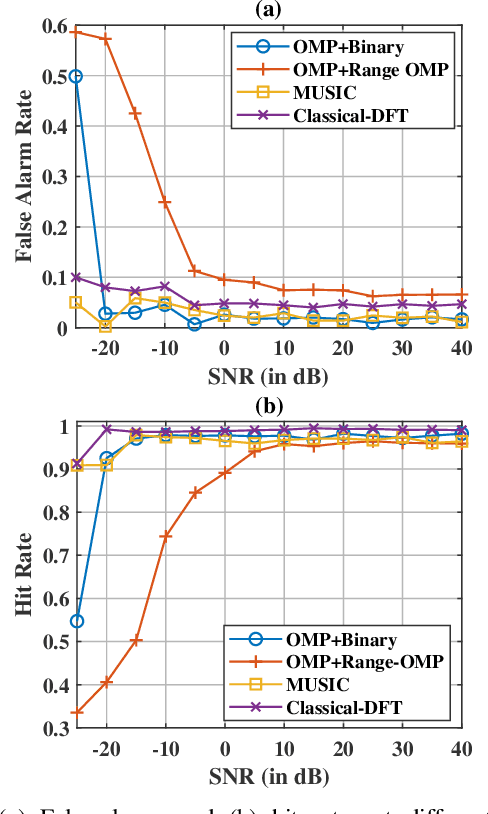
Multiple-input multiple-output (MIMO) radar offers several performance and flexibility advantages over traditional radar arrays. However, high angular and Doppler resolutions necessitate a large number of antenna elements and the transmission of numerous chirps, leading to increased hardware and computational complexity. While compressive sensing (CS) has recently been applied to pulsed-waveform radars with sparse measurements, its application to frequency-modulated continuous wave (FMCW) radar for target detection remains largely unexplored. In this paper, we propose a novel CS-based multi-target localization algorithm in the range, Doppler, and angular domains for MIMO-FMCW radar, where we jointly estimate targets' velocities and angles of arrival. To this end, we present a signal model for sparse-random and uniform linear arrays based on three-dimensional spectral estimation. For range estimation, we propose a discrete Fourier transform (DFT)-based focusing and orthogonal matching pursuit (OMP)-based techniques, each with distinct advantages, while two-dimensional CS is used for joint Doppler-angle estimation. Leveraging the properties of structured random matrices, we establish theoretical uniform and non-uniform recovery guarantees with high probability for the proposed framework. Our numerical experiments demonstrate that our methods achieve similar detection performance and higher resolution compared to conventional DFT and MUSIC with fewer transmitted chirps and antenna elements.