Multi-target Range, Doppler and Angle estimation in MIMO-FMCW Radar with Limited Measurements

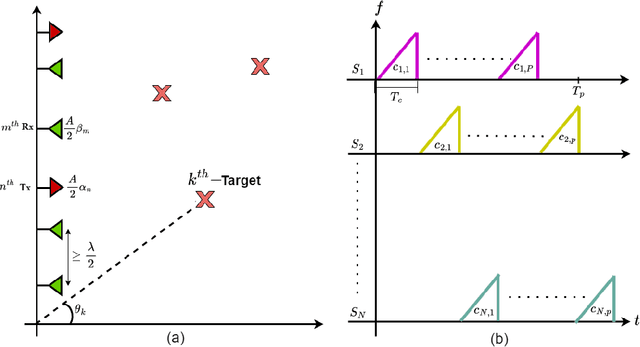
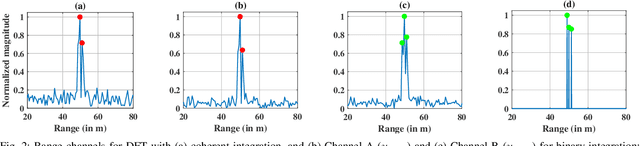
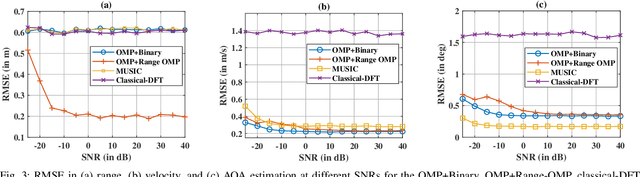
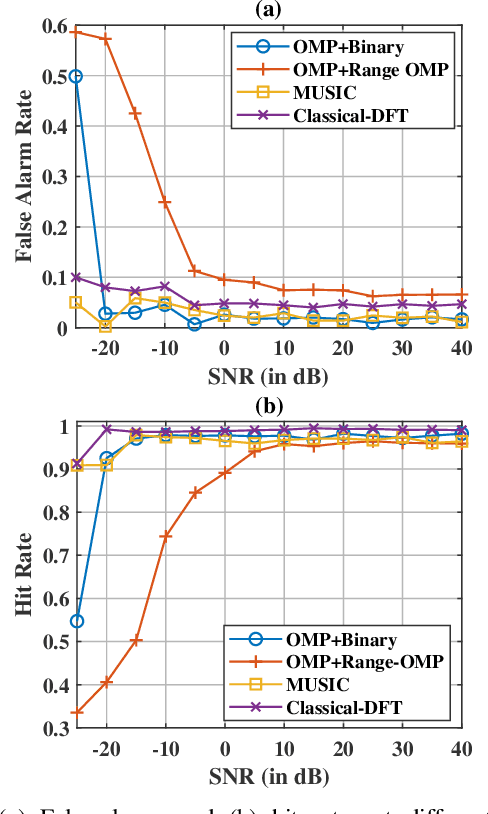
Multiple-input multiple-output (MIMO) radar offers several performance and flexibility advantages over traditional radar arrays. However, high angular and Doppler resolutions necessitate a large number of antenna elements and the transmission of numerous chirps, leading to increased hardware and computational complexity. While compressive sensing (CS) has recently been applied to pulsed-waveform radars with sparse measurements, its application to frequency-modulated continuous wave (FMCW) radar for target detection remains largely unexplored. In this paper, we propose a novel CS-based multi-target localization algorithm in the range, Doppler, and angular domains for MIMO-FMCW radar, where we jointly estimate targets' velocities and angles of arrival. To this end, we present a signal model for sparse-random and uniform linear arrays based on three-dimensional spectral estimation. For range estimation, we propose a discrete Fourier transform (DFT)-based focusing and orthogonal matching pursuit (OMP)-based techniques, each with distinct advantages, while two-dimensional CS is used for joint Doppler-angle estimation. Leveraging the properties of structured random matrices, we establish theoretical uniform and non-uniform recovery guarantees with high probability for the proposed framework. Our numerical experiments demonstrate that our methods achieve similar detection performance and higher resolution compared to conventional DFT and MUSIC with fewer transmitted chirps and antenna elements.

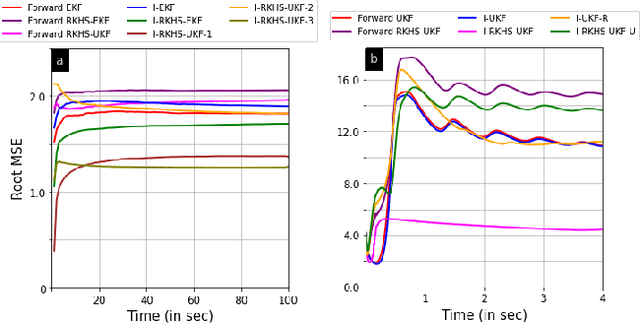
Inverse Particle and Ensemble Kalman Filters

In cognitive systems, recent emphasis has been placed on studying cognitive processes of the subject whose behavior was the primary focus of the system's cognitive response. This approach, known as inverse cognition, arises in counter-adversarial applications and has motivated the development of inverse Bayesian filters. In this context, a cognitive adversary, such as a radar, uses a forward Bayesian filter to track its target of interest. An inverse filter is then employed to infer adversary's estimate of target's or defender's state. Previous studies have addressed this inverse filtering problem by introducing methods like inverse Kalman filter (I-KF), inverse extended KF (I-EKF), and inverse unscented KF (I-UKF). However, these inverse filters assume additive Gaussian noises and/or rely on local approximations of non-linear dynamics at the state estimates, limiting their practical application. Contrarily, this paper adopts a global filtering approach and develops an inverse particle filter (I-PF). The particle filter framework employs Monte Carlo (MC) methods to approximate arbitrary posterior distributions. Moreover, under mild system-level conditions, the proposed I-PF demonstrates convergence to the optimal inverse filter. Additionally, we explore MC techniques to approximate Gaussian posteriors and introduce inverse Gaussian PF (I-GPF) and inverse ensemble KF (I-EnKF). Our I-GPF and I-EnKF can efficiently handle non-Gaussian noises with suitable modifications. Additionally, we propose the differentiable I-PF, differentiable I-EnKF, and reproducing kernel Hilbert space-based EnKF (RKHS-EnKF) methods to address scenarios where system information is unknown to defender. Using recursive Cram\'er-Rao lower bound and non-credibility index (NCI), our numerical experiments for different applications demonstrate the estimation performance and time complexity of the proposed filters.

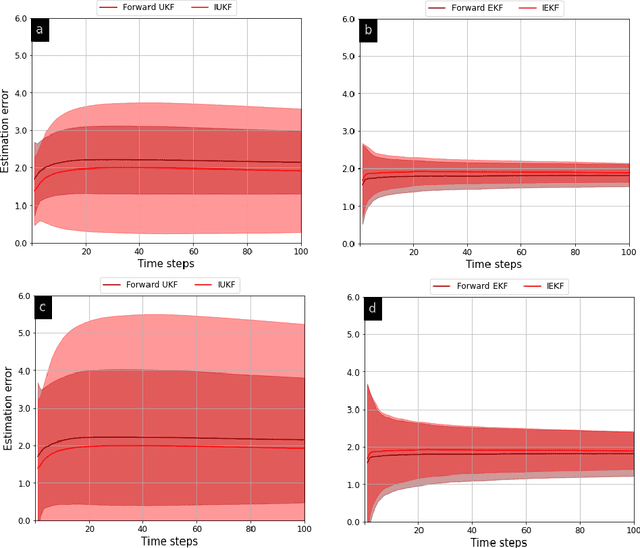
Inverse Unscented Kalman Filter

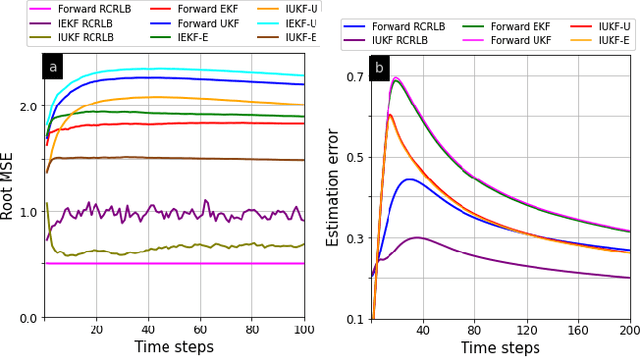
Rapid advances in designing cognitive and counter-adversarial systems have motivated the development of inverse Bayesian filters. In this setting, a cognitive `adversary' tracks its target of interest via a stochastic framework such as a Kalman filter (KF). The target or `defender' then employs another inverse stochastic filter to infer the forward filter estimates of the defender computed by the adversary. For linear systems, inverse Kalman filter (I-KF) has been recently shown to be effective in these counter-adversarial applications. In the paper, contrary to prior works, we focus on non-linear system dynamics and formulate the inverse unscented KF (I-UKF) to estimate the defender's state with reduced linearization errors. We then generalize this framework to an unknown system model by proposing reproducing kernel Hilbert space-based UKF (RKHS-UKF) to learn the system dynamics and estimate the state based on its observations. Our theoretical analyses to guarantee the stochastic stability of I-UKF and RKHS-UKF in the mean-squared sense shows that, provided the forward filters are stable, the inverse filters are also stable under mild system-level conditions. Our numerical experiments for several different applications demonstrate the state estimation performance of the proposed filters using recursive Cram\'{e}r-Rao lower bound as a benchmark.

Inverse Cubature and Quadrature Kalman filters

Recent developments in counter-adversarial system research have led to the development of inverse stochastic filters that are employed by a defender to infer the information its adversary may have learned. Prior works addressed this inverse cognition problem by proposing inverse Kalman filter (I-KF) and inverse extended KF (I-EKF), respectively, for linear and non-linear Gaussian state-space models. However, in practice, many counter-adversarial settings involve highly non-linear system models, wherein EKF's linearization often fails. In this paper, we consider the efficient numerical integration techniques to address such nonlinearities and, to this end, develop inverse cubature KF (I-CKF) and inverse quadrature KF (I-QKF). We derive the stochastic stability conditions for the proposed filters in the exponential-mean-squared-boundedness sense. Numerical experiments demonstrate the estimation accuracy of our I-CKF and I-QKF with the recursive Cram\'{e}r-Rao lower bound as a benchmark.

Multi-target Range and Angle detection for MIMO-FMCW radar with limited antennas

Multiple-input multiple-output (MIMO) radar has several advantages with respect to the traditional radar array systems in terms of performance and flexibility. However, in order to achieve high angular resolution, a MIMO radar requires a large number of transmit and receive antennas, which increases hardware design and computational complexities. Although spatial compressive sensing (CS) has been recently considered for a pulsed-waveform MIMO radar with sparse random arrays, such methods for the frequency-modulated continuous wave (FMCW) radar remain largely unexplored. In this context, we propose a novel multi-target localization algorithm in the range-angle domain for a MIMO FMCW radar with a sparse array of randomly placed transmit and receive elements. In particular, we first obtain the targets' range-delays using a discrete Fourier transform (DFT)-based focusing operation. The target angles are then recovered at each detected range using CS-based techniques exploiting the sparsity of the target scene. Our simulation results demonstrate the effectiveness of the proposed algorithm over the classical methods in detecting multiple targets with a sparse array.

Counter-Adversarial Learning with Inverse Unscented Kalman Filter

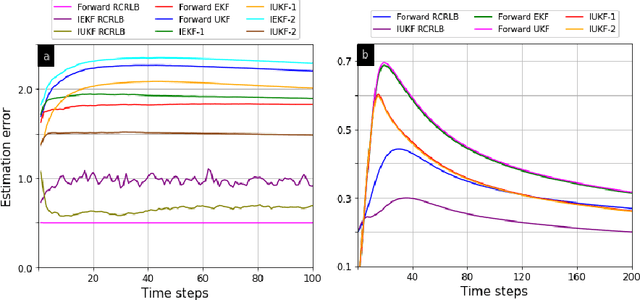
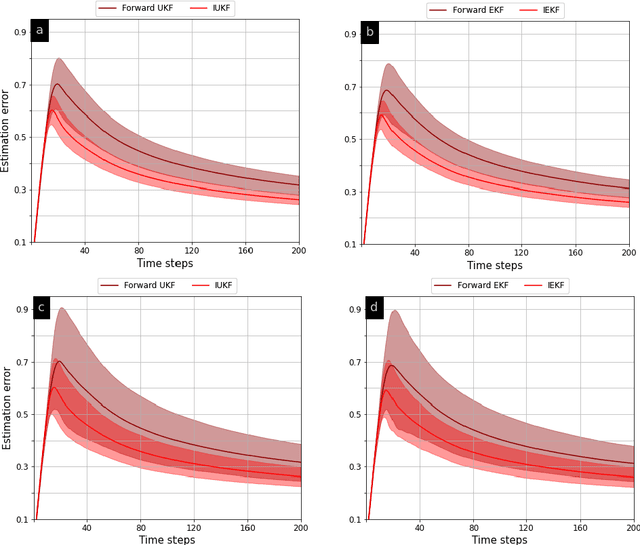
In order to infer the strategy of an intelligent attacker, it is desired for the defender to cognitively sense the attacker's state. In this context, we aim to learn the information that an adversary has gathered about us from a Bayesian perspective. Prior works employ linear Gaussian state-space models and solve this inverse cognition problem through the design of inverse stochastic filters. In practice, these counter-adversarial settings are highly nonlinear systems. We address this by formulating the inverse cognition as a nonlinear Gaussian state-space model, wherein the adversary employs an unscented Kalman filter (UKF) to estimate our state with reduced linearization errors. To estimate the adversary's estimate of us, we propose and develop an inverse UKF (IUKF), wherein the system model is known to both the adversary and the defender. We also derive the conditions for the stochastic stability of IUKF in the mean-squared boundedness sense. Numerical experiments for multiple practical system models show that the estimation error of IUKF converges and closely follows the recursive Cram\'{e}r-Rao lower bound.

Inverse Extended Kalman Filter -- Part II: Highly Non-Linear and Uncertain Systems

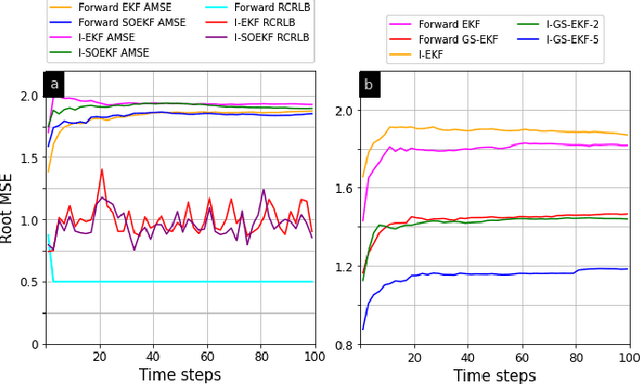
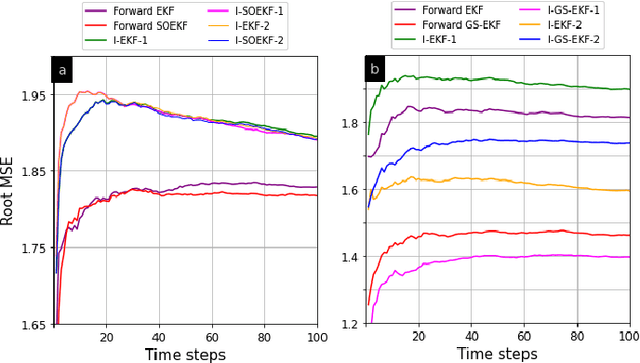
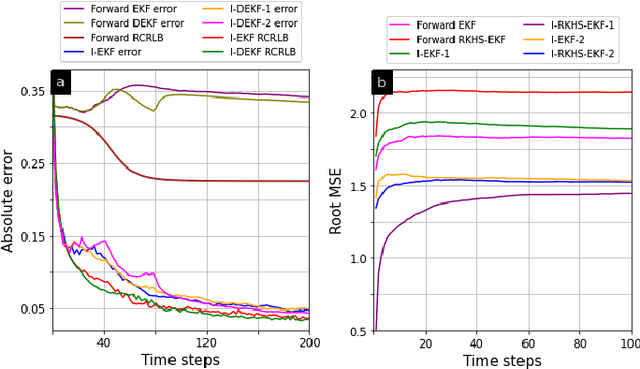
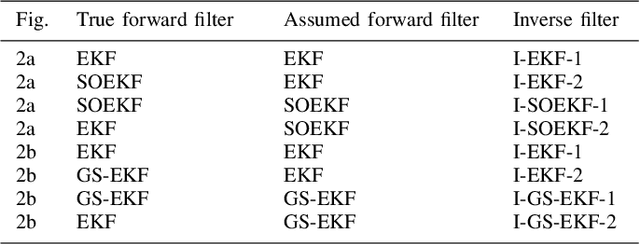
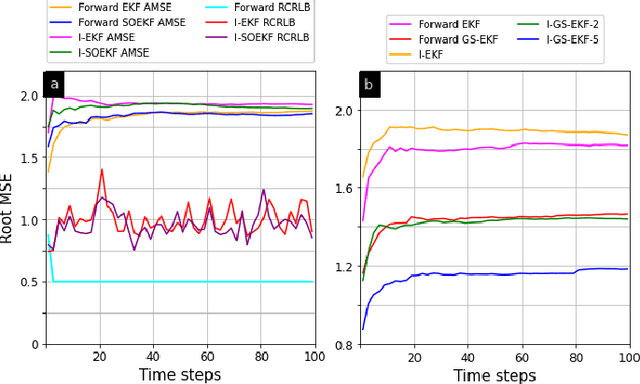
Recent counter-adversarial system design problems have motivated the development of inverse Bayesian filters. For example, inverse Kalman filter (I-KF) has been recently formulated to estimate the adversary's Kalman filter tracked estimates and hence, predict the adversary's future steps. The purpose of this paper and the companion paper (Part I) is to address the inverse filtering problem in non-linear systems by proposing an inverse extended Kalman filter (I-EKF). In a companion paper (Part I), we developed the theory of I-EKF (with and without unknown inputs) and I-KF (with unknown inputs). In this paper, we develop this theory for highly non-linear models, which employ second-order, Gaussian sum, and dithered forward EKFs. In particular, we derive theoretical stability guarantees for the inverse second-order EKF using the bounded non-linearity approach. To address the limitation of the standard I-EKFs that the system model and forward filter are perfectly known to the defender, we propose reproducing kernel Hilbert space-based EKF to learn the unknown system dynamics based on its observations, which can be employed as an inverse filter to infer the adversary's estimate. Numerical experiments demonstrate the state estimation performance of the proposed filters using recursive Cram\'{e}r-Rao lower bound as a benchmark.

Inverse Extended Kalman Filter

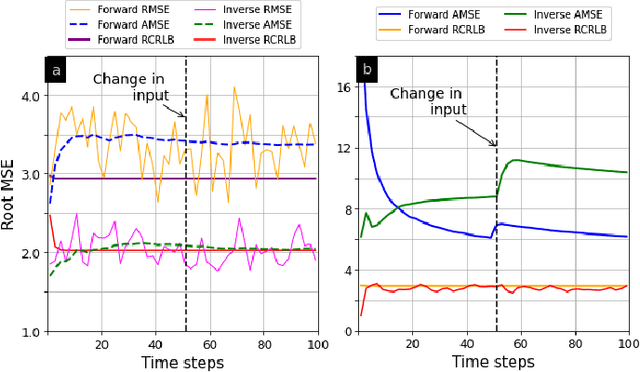
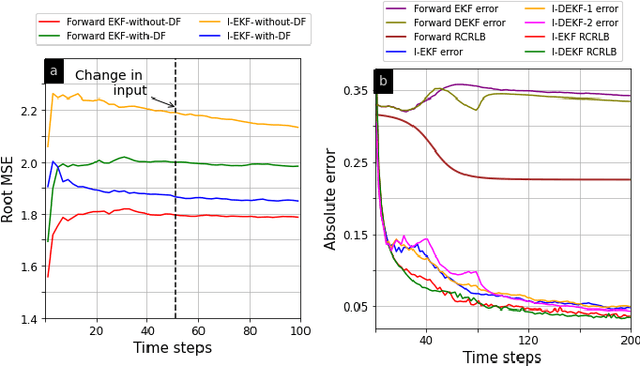
Recent advances in counter-adversarial systems have garnered significant research interest in inverse filtering from a Bayesian perspective. For example, interest in estimating the adversary's Kalman filter tracked estimate with the purpose of predicting the adversary's future steps has led to recent formulations of inverse Kalman filter (I-KF). In this context of inverse filtering, we address the key challenges of nonlinear process dynamics and unknown input to the forward filter by proposing inverse extended Kalman filter (I-EKF). We derive I-EKF with and without an unknown input by considering nonlinearity in both forward and inverse state-space models. In the process, I-KF-with-unknown-input is also obtained. We then provide theoretical stability guarantees using both bounded nonlinearity and unknown matrix approaches. We further generalize these formulations and results to the case of higher-order, Gaussian-sum, and dithered I-EKFs. Numerical experiments validate our methods for various proposed inverse filters using the recursive Cram\'er-Rao lower bound as a benchmark.