Counter-Adversarial Learning with Inverse Unscented Kalman Filter

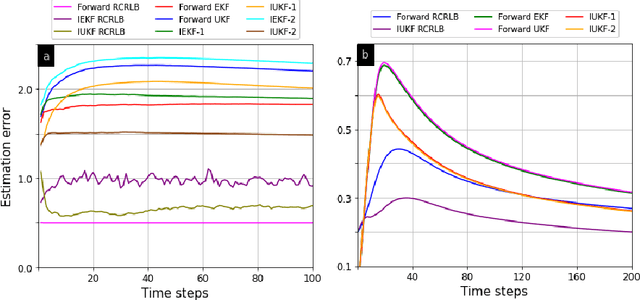
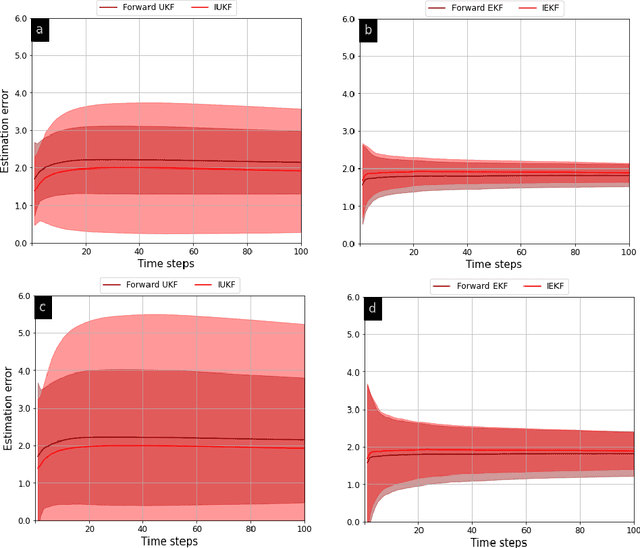
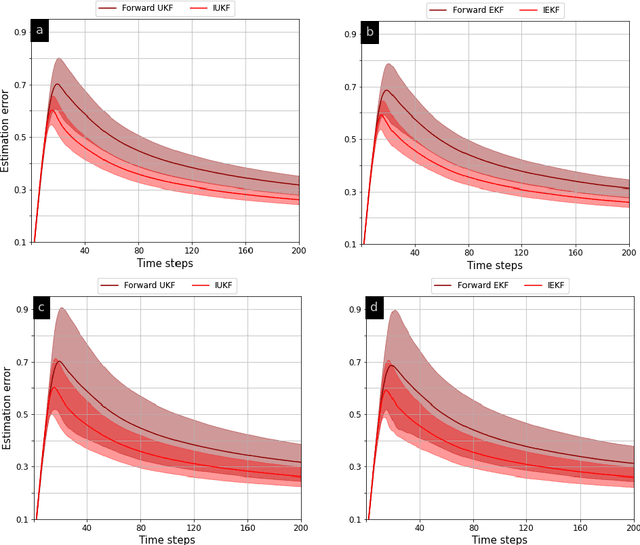
In order to infer the strategy of an intelligent attacker, it is desired for the defender to cognitively sense the attacker's state. In this context, we aim to learn the information that an adversary has gathered about us from a Bayesian perspective. Prior works employ linear Gaussian state-space models and solve this inverse cognition problem through the design of inverse stochastic filters. In practice, these counter-adversarial settings are highly nonlinear systems. We address this by formulating the inverse cognition as a nonlinear Gaussian state-space model, wherein the adversary employs an unscented Kalman filter (UKF) to estimate our state with reduced linearization errors. To estimate the adversary's estimate of us, we propose and develop an inverse UKF (IUKF), wherein the system model is known to both the adversary and the defender. We also derive the conditions for the stochastic stability of IUKF in the mean-squared boundedness sense. Numerical experiments for multiple practical system models show that the estimation error of IUKF converges and closely follows the recursive Cram\'{e}r-Rao lower bound.