Inverse Unscented Kalman Filter

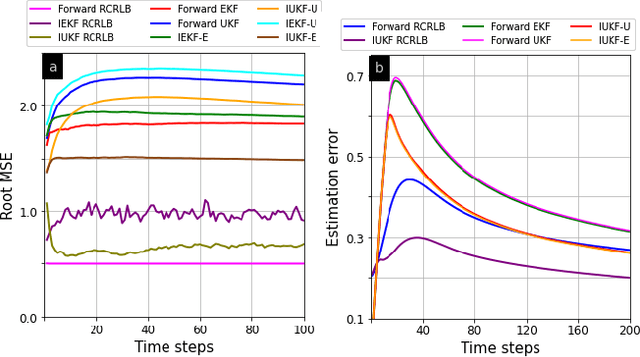
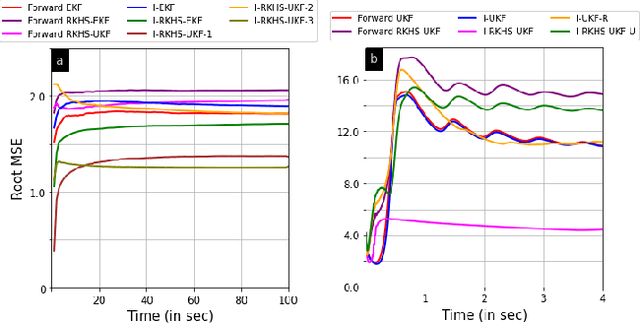
Rapid advances in designing cognitive and counter-adversarial systems have motivated the development of inverse Bayesian filters. In this setting, a cognitive `adversary' tracks its target of interest via a stochastic framework such as a Kalman filter (KF). The target or `defender' then employs another inverse stochastic filter to infer the forward filter estimates of the defender computed by the adversary. For linear systems, inverse Kalman filter (I-KF) has been recently shown to be effective in these counter-adversarial applications. In the paper, contrary to prior works, we focus on non-linear system dynamics and formulate the inverse unscented KF (I-UKF) to estimate the defender's state with reduced linearization errors. We then generalize this framework to an unknown system model by proposing reproducing kernel Hilbert space-based UKF (RKHS-UKF) to learn the system dynamics and estimate the state based on its observations. Our theoretical analyses to guarantee the stochastic stability of I-UKF and RKHS-UKF in the mean-squared sense shows that, provided the forward filters are stable, the inverse filters are also stable under mild system-level conditions. Our numerical experiments for several different applications demonstrate the state estimation performance of the proposed filters using recursive Cram\'{e}r-Rao lower bound as a benchmark.