Faster Machine Translation Ensembling with Reinforcement Learning and Competitive Correction

Ensembling neural machine translation (NMT) models to produce higher-quality translations than the $L$ individual models has been extensively studied. Recent methods typically employ a candidate selection block (CSB) and an encoder-decoder fusion block (FB), requiring inference across \textit{all} candidate models, leading to significant computational overhead, generally $\Omega(L)$. This paper introduces \textbf{SmartGen}, a reinforcement learning (RL)-based strategy that improves the CSB by selecting a small, fixed number of candidates and identifying optimal groups to pass to the fusion block for each input sentence. Furthermore, previously, the CSB and FB were trained independently, leading to suboptimal NMT performance. Our DQN-based \textbf{SmartGen} addresses this by using feedback from the FB block as a reward during training. We also resolve a key issue in earlier methods, where candidates were passed to the FB without modification, by introducing a Competitive Correction Block (CCB). Finally, we validate our approach with extensive experiments on English-Hindi translation tasks in both directions.

Enhancing Entertainment Translation for Indian Languages using Adaptive Context, Style and LLMs

We address the challenging task of neural machine translation (NMT) in the entertainment domain, where the objective is to automatically translate a given dialogue from a source language content to a target language. This task has various applications, particularly in automatic dubbing, subtitling, and other content localization tasks, enabling source content to reach a wider audience. Traditional NMT systems typically translate individual sentences in isolation, without facilitating knowledge transfer of crucial elements such as the context and style from previously encountered sentences. In this work, we emphasize the significance of these fundamental aspects in producing pertinent and captivating translations. We demonstrate their significance through several examples and propose a novel framework for entertainment translation, which, to our knowledge, is the first of its kind. Furthermore, we introduce an algorithm to estimate the context and style of the current session and use these estimations to generate a prompt that guides a Large Language Model (LLM) to generate high-quality translations. Our method is both language and LLM-agnostic, making it a general-purpose tool. We demonstrate the effectiveness of our algorithm through various numerical studies and observe significant improvement in the COMET scores over various state-of-the-art LLMs. Moreover, our proposed method consistently outperforms baseline LLMs in terms of win-ratio.

Isometric Neural Machine Translation using Phoneme Count Ratio Reward-based Reinforcement Learning

Traditional Automatic Video Dubbing (AVD) pipeline consists of three key modules, namely, Automatic Speech Recognition (ASR), Neural Machine Translation (NMT), and Text-to-Speech (TTS). Within AVD pipelines, isometric-NMT algorithms are employed to regulate the length of the synthesized output text. This is done to guarantee synchronization with respect to the alignment of video and audio subsequent to the dubbing process. Previous approaches have focused on aligning the number of characters and words in the source and target language texts of Machine Translation models. However, our approach aims to align the number of phonemes instead, as they are closely associated with speech duration. In this paper, we present the development of an isometric NMT system using Reinforcement Learning (RL), with a focus on optimizing the alignment of phoneme counts in the source and target language sentence pairs. To evaluate our models, we propose the Phoneme Count Compliance (PCC) score, which is a measure of length compliance. Our approach demonstrates a substantial improvement of approximately 36% in the PCC score compared to the state-of-the-art models when applied to English-Hindi language pairs. Moreover, we propose a student-teacher architecture within the framework of our RL approach to maintain a trade-off between the phoneme count and translation quality.

Actor-Critic based Improper Reinforcement Learning

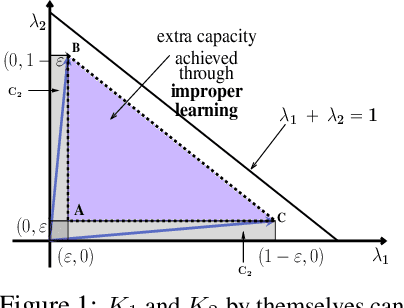
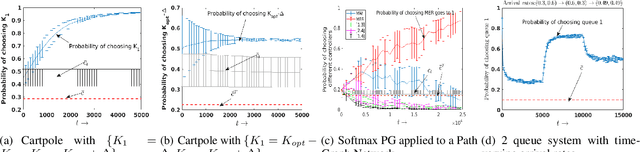
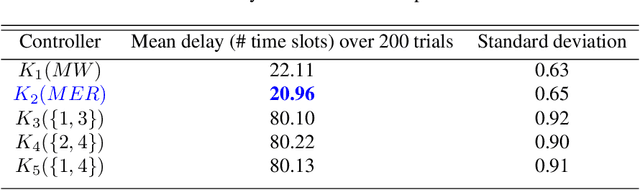
We consider an improper reinforcement learning setting where a learner is given $M$ base controllers for an unknown Markov decision process, and wishes to combine them optimally to produce a potentially new controller that can outperform each of the base ones. This can be useful in tuning across controllers, learnt possibly in mismatched or simulated environments, to obtain a good controller for a given target environment with relatively few trials. Towards this, we propose two algorithms: (1) a Policy Gradient-based approach; and (2) an algorithm that can switch between a simple Actor-Critic (AC) based scheme and a Natural Actor-Critic (NAC) scheme depending on the available information. Both algorithms operate over a class of improper mixtures of the given controllers. For the first case, we derive convergence rate guarantees assuming access to a gradient oracle. For the AC-based approach we provide convergence rate guarantees to a stationary point in the basic AC case and to a global optimum in the NAC case. Numerical results on (i) the standard control theoretic benchmark of stabilizing an cartpole; and (ii) a constrained queueing task show that our improper policy optimization algorithm can stabilize the system even when the base policies at its disposal are unstable.

Improper Learning with Gradient-based Policy Optimization

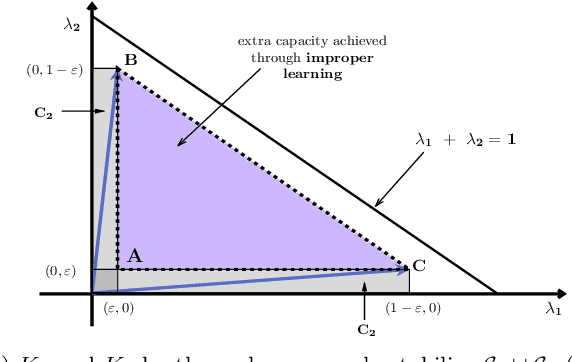
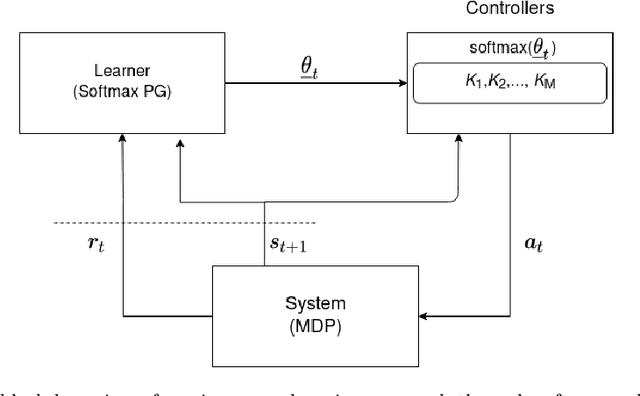
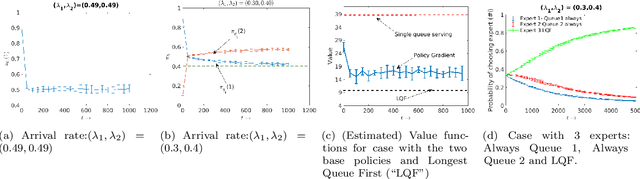
We consider an improper reinforcement learning setting where the learner is given M base controllers for an unknown Markov Decision Process, and wishes to combine them optimally to produce a potentially new controller that can outperform each of the base ones. We propose a gradient-based approach that operates over a class of improper mixtures of the controllers. The value function of the mixture and its gradient may not be available in closed-form; however, we show that we can employ rollouts and simultaneous perturbation stochastic approximation (SPSA) for explicit gradient descent optimization. We derive convergence and convergence rate guarantees for the approach assuming access to a gradient oracle. Numerical results on a challenging constrained queueing task show that our improper policy optimization algorithm can stabilize the system even when each constituent policy at its disposal is unstable.

Explicit Best Arm Identification in Linear Bandits Using No-Regret Learners

We study the problem of best arm identification in linearly parameterised multi-armed bandits. Given a set of feature vectors $\mathcal{X}\subset\mathbb{R}^d,$ a confidence parameter $\delta$ and an unknown vector $\theta^*,$ the goal is to identify $\arg\max_{x\in\mathcal{X}}x^T\theta^*$, with probability at least $1-\delta,$ using noisy measurements of the form $x^T\theta^*.$ For this fixed confidence ($\delta$-PAC) setting, we propose an explicitly implementable and provably order-optimal sample-complexity algorithm to solve this problem. Previous approaches rely on access to minimax optimization oracles. The algorithm, which we call the \textit{Phased Elimination Linear Exploration Game} (PELEG), maintains a high-probability confidence ellipsoid containing $\theta^*$ in each round and uses it to eliminate suboptimal arms in phases. PELEG achieves fast shrinkage of this confidence ellipsoid along the most confusing (i.e., close to, but not optimal) directions by interpreting the problem as a two player zero-sum game, and sequentially converging to its saddle point using low-regret learners to compute players' strategies in each round. We analyze the sample complexity of PELEG and show that it matches, up to order, an instance-dependent lower bound on sample complexity in the linear bandit setting. We also provide numerical results for the proposed algorithm consistent with its theoretical guarantees.

Towards Optimal and Efficient Best Arm Identification in Linear Bandits

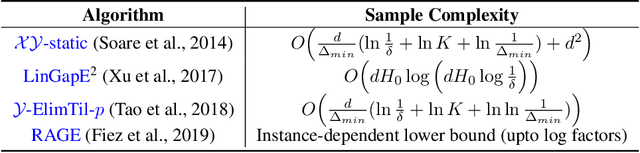
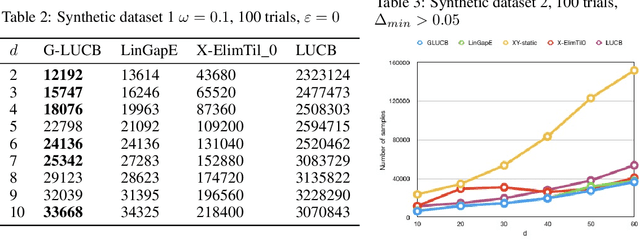
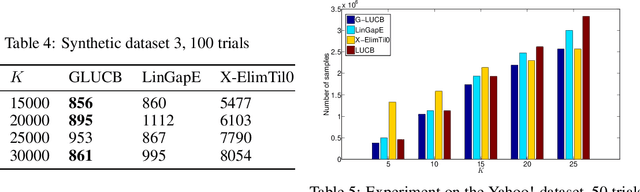
We give a new algorithm for best arm identification in linearly parameterised bandits in the fixed confidence setting. The algorithm generalises the well-known LUCB algorithm of Kalyanakrishnan et al. (2012) by playing an arm which minimises a suitable notion of geometric overlap of the statistical confidence set for the unknown parameter, and is fully adaptive and computationally efficient as compared to several state-of-the methods. We theoretically analyse the sample complexity of the algorithm for problems with two and three arms, showing optimality in many cases. Numerical results indicate favourable performance over other algorithms with which we compare.

Low-rank Bandits with Latent Mixtures

We study the task of maximizing rewards from recommending items (actions) to users sequentially interacting with a recommender system. Users are modeled as latent mixtures of C many representative user classes, where each class specifies a mean reward profile across actions. Both the user features (mixture distribution over classes) and the item features (mean reward vector per class) are unknown a priori. The user identity is the only contextual information available to the learner while interacting. This induces a low-rank structure on the matrix of expected rewards r a,b from recommending item a to user b. The problem reduces to the well-known linear bandit when either user or item-side features are perfectly known. In the setting where each user, with its stochastically sampled taste profile, interacts only for a small number of sessions, we develop a bandit algorithm for the two-sided uncertainty. It combines the Robust Tensor Power Method of Anandkumar et al. (2014b) with the OFUL linear bandit algorithm of Abbasi-Yadkori et al. (2011). We provide the first rigorous regret analysis of this combination, showing that its regret after T user interactions is $\tilde O(C\sqrt{BT})$, with B the number of users. An ingredient towards this result is a novel robustness property of OFUL, of independent interest.