Improper Learning with Gradient-based Policy Optimization
Paper and Code
Feb 21, 2021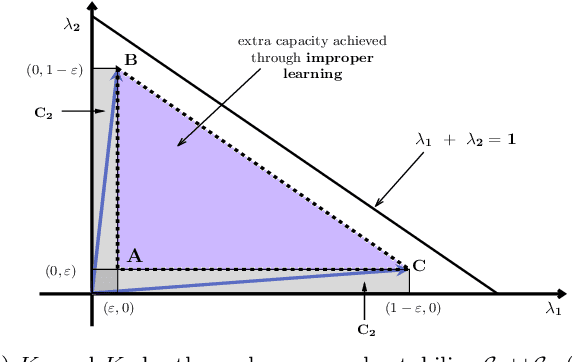
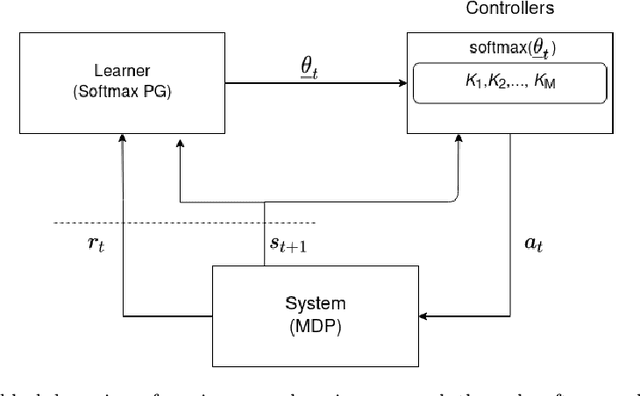
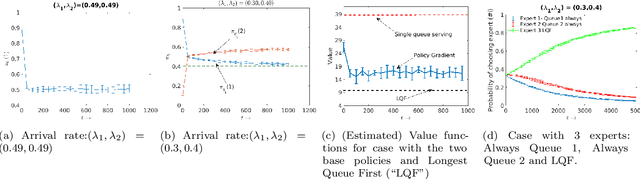
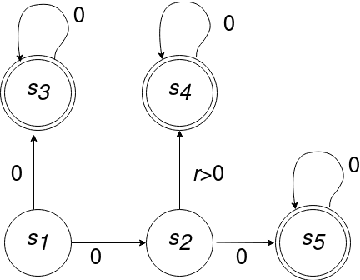
We consider an improper reinforcement learning setting where the learner is given M base controllers for an unknown Markov Decision Process, and wishes to combine them optimally to produce a potentially new controller that can outperform each of the base ones. We propose a gradient-based approach that operates over a class of improper mixtures of the controllers. The value function of the mixture and its gradient may not be available in closed-form; however, we show that we can employ rollouts and simultaneous perturbation stochastic approximation (SPSA) for explicit gradient descent optimization. We derive convergence and convergence rate guarantees for the approach assuming access to a gradient oracle. Numerical results on a challenging constrained queueing task show that our improper policy optimization algorithm can stabilize the system even when each constituent policy at its disposal is unstable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge