Approximate Q-learning and SARSA under the $ε$-greedy Policy: a Differential Inclusion Analysis

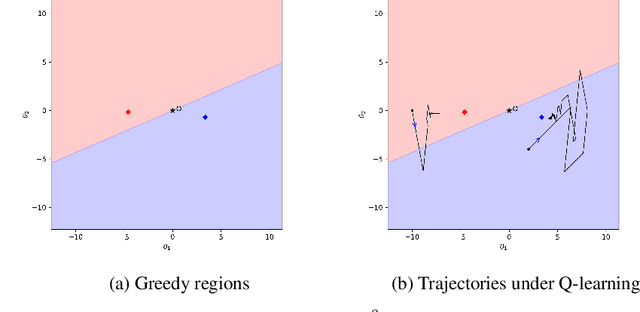
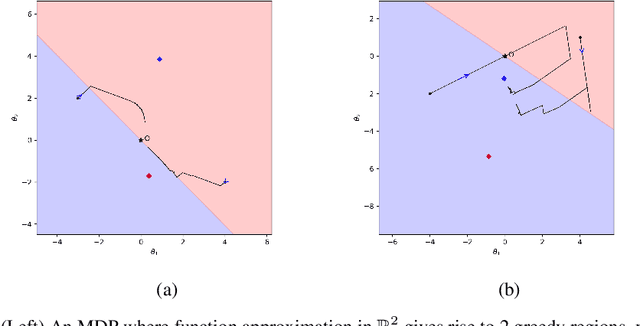
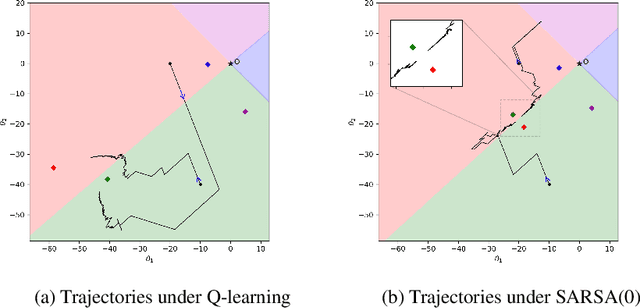
Q-learning and SARSA(0) with linear function approximation, under $\epsilon$-greedy exploration, are leading methods to estimate the optimal policy in Reinforcement Learning (RL). It has been empirically known that the discontinuous nature of the greedy policies causes these algorithms to exhibit complex phenomena such as i.) instability, ii.) policy oscillation and chattering, iii.) multiple attractors, and iv.) worst policy convergence. However, the literature lacks a formal recipe to explain these behaviors and this has been a long-standing open problem (Sutton, 1999). Our work addresses this by building the necessary mathematical framework using stochastic recursive inclusions and Differential Inclusions (DIs). From this novel viewpoint, our main result states that these approximate algorithms asymptotically converge to suitable invariant sets of DIs instead of differential equations, as is common elsewhere in RL. Furthermore, the nature of these deterministic DIs completely governs the limiting behaviors of these algorithms.