Better-than-KL PAC-Bayes Bounds

Let $f(\theta, X_1),$ $ \dots,$ $ f(\theta, X_n)$ be a sequence of random elements, where $f$ is a fixed scalar function, $X_1, \dots, X_n$ are independent random variables (data), and $\theta$ is a random parameter distributed according to some data-dependent posterior distribution $P_n$. In this paper, we consider the problem of proving concentration inequalities to estimate the mean of the sequence. An example of such a problem is the estimation of the generalization error of some predictor trained by a stochastic algorithm, such as a neural network where $f$ is a loss function. Classically, this problem is approached through a PAC-Bayes analysis where, in addition to the posterior, we choose a prior distribution which captures our belief about the inductive bias of the learning problem. Then, the key quantity in PAC-Bayes concentration bounds is a divergence that captures the complexity of the learning problem where the de facto standard choice is the KL divergence. However, the tightness of this choice has rarely been questioned. In this paper, we challenge the tightness of the KL-divergence-based bounds by showing that it is possible to achieve a strictly tighter bound. In particular, we demonstrate new high-probability PAC-Bayes bounds with a novel and better-than-KL divergence that is inspired by Zhang et al. (2022). Our proof is inspired by recent advances in regret analysis of gambling algorithms, and its use to derive concentration inequalities. Our result is first-of-its-kind in that existing PAC-Bayes bounds with non-KL divergences are not known to be strictly better than KL. Thus, we believe our work marks the first step towards identifying optimal rates of PAC-Bayes bounds.

Differentially Private Episodic Reinforcement Learning with Heavy-tailed Rewards

In this paper, we study the problem of (finite horizon tabular) Markov decision processes (MDPs) with heavy-tailed rewards under the constraint of differential privacy (DP). Compared with the previous studies for private reinforcement learning that typically assume rewards are sampled from some bounded or sub-Gaussian distributions to ensure DP, we consider the setting where reward distributions have only finite $(1+v)$-th moments with some $v \in (0,1]$. By resorting to robust mean estimators for rewards, we first propose two frameworks for heavy-tailed MDPs, i.e., one is for value iteration and another is for policy optimization. Under each framework, we consider both joint differential privacy (JDP) and local differential privacy (LDP) models. Based on our frameworks, we provide regret upper bounds for both JDP and LDP cases and show that the moment of distribution and privacy budget both have significant impacts on regrets. Finally, we establish a lower bound of regret minimization for heavy-tailed MDPs in JDP model by reducing it to the instance-independent lower bound of heavy-tailed multi-armed bandits in DP model. We also show the lower bound for the problem in LDP by adopting some private minimax methods. Our results reveal that there are fundamental differences between the problem of private RL with sub-Gaussian and that with heavy-tailed rewards.

Quantum Computing Provides Exponential Regret Improvement in Episodic Reinforcement Learning

In this paper, we investigate the problem of \textit{episodic reinforcement learning} with quantum oracles for state evolution. To this end, we propose an \textit{Upper Confidence Bound} (UCB) based quantum algorithmic framework to facilitate learning of a finite-horizon MDP. Our quantum algorithm achieves an exponential improvement in regret as compared to the classical counterparts, achieving a regret of $\Tilde{\mathcal{O}}(1)$ as compared to $\Tilde{\mathcal{O}}(\sqrt{K})$ \footnote{$\Tilde{\mathcal{O}}(\cdot)$ hides logarithmic terms.}, $K$ being the number of training episodes. In order to achieve this advantage, we exploit efficient quantum mean estimation technique that provides quadratic improvement in the number of i.i.d. samples needed to estimate the mean of sub-Gaussian random variables as compared to classical mean estimation. This improvement is a key to the significant regret improvement in quantum reinforcement learning. We provide proof-of-concept experiments on various RL environments that in turn demonstrate performance gains of the proposed algorithmic framework.

On Private and Robust Bandits

We study private and robust multi-armed bandits (MABs), where the agent receives Huber's contaminated heavy-tailed rewards and meanwhile needs to ensure differential privacy. We first present its minimax lower bound, characterizing the information-theoretic limit of regret with respect to privacy budget, contamination level and heavy-tailedness. Then, we propose a meta-algorithm that builds on a private and robust mean estimation sub-routine \texttt{PRM} that essentially relies on reward truncation and the Laplace mechanism only. For two different heavy-tailed settings, we give specific schemes of \texttt{PRM}, which enable us to achieve nearly-optimal regret. As by-products of our main results, we also give the first minimax lower bound for private heavy-tailed MABs (i.e., without contamination). Moreover, our two proposed truncation-based \texttt{PRM} achieve the optimal trade-off between estimation accuracy, privacy and robustness. Finally, we support our theoretical results with experimental studies.

Quantum Heavy-tailed Bandits

In this paper, we study multi-armed bandits (MAB) and stochastic linear bandits (SLB) with heavy-tailed rewards and quantum reward oracle. Unlike the previous work on quantum bandits that assumes bounded/sub-Gaussian distributions for rewards, here we investigate the quantum bandits problem under a weaker assumption that the distributions of rewards only have bounded $(1+v)$-th moment for some $v\in (0,1]$. In order to achieve regret improvements for heavy-tailed bandits, we first propose a new quantum mean estimator for heavy-tailed distributions, which is based on the Quantum Monte Carlo Mean Estimator and achieves a quadratic improvement of estimation error compared to the classical one. Based on our quantum mean estimator, we focus on quantum heavy-tailed MAB and SLB and propose quantum algorithms based on the Upper Confidence Bound (UCB) framework for both problems with $\Tilde{O}(T^{\frac{1-v}{1+v}})$ regrets, polynomially improving the dependence in terms of $T$ as compared to classical (near) optimal regrets of $\Tilde{O}(T^{\frac{1}{1+v}})$, where $T$ is the number of rounds. Finally, experiments also support our theoretical results and show the effectiveness of our proposed methods.

Optimal Rates of (Locally) Differentially Private Heavy-tailed Multi-Armed Bandits

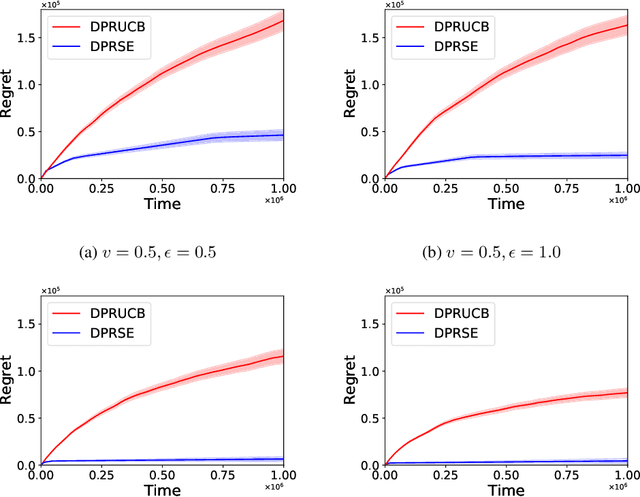
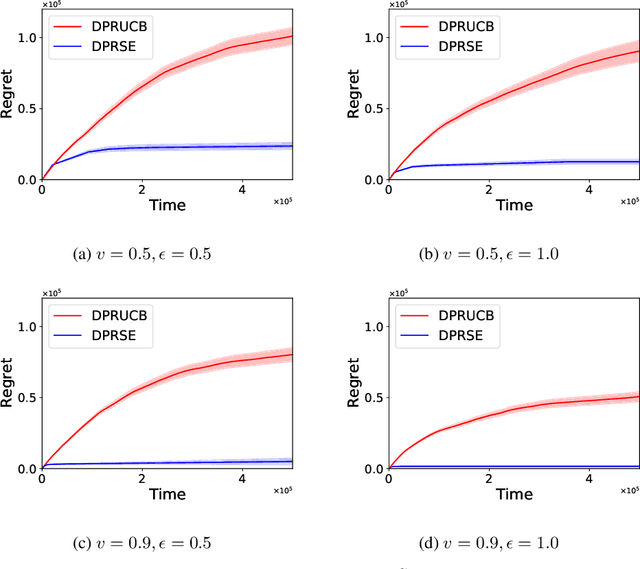
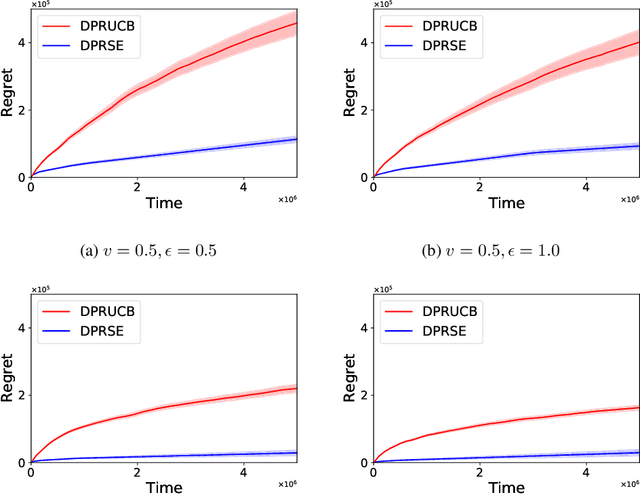
In this paper we study the problem of stochastic multi-armed bandits (MAB) in the (local) differential privacy (DP/LDP) model. Unlike the previous results which need to assume bounded reward distributions, here we mainly focus on the case the reward distribution of each arm only has $(1+v)$-th moment with some $v\in (0, 1]$. In the first part, we study the problem in the central $\epsilon$-DP model. We first provide a near-optimal result by developing a private and robust Upper Confidence Bound (UCB) algorithm. Then, we improve the result via a private and robust version of the Successive Elimination (SE) algorithm. Finally, we show that the instance-dependent regret bound of our improved algorithm is optimal by showing its lower bound. In the second part of the paper, we study the problem in the $\epsilon$-LDP model. We propose an algorithm which could be seen as locally private and robust version of the SE algorithm, and show it could achieve (near) optimal rates for both instance-dependent and instance-independent regrets. All of the above results can also reveal the differences between the problem of private MAB with bounded rewards and heavy-tailed rewards. To achieve these (near) optimal rates, we develop several new hard instances and private robust estimators as byproducts, which might could be used to other related problems. Finally, experimental results also support our theoretical analysis and show the effectiveness of our algorithms.