Scale-Invariant Fast Convergence in Games

Scale-invariance in games has recently emerged as a widely valued desirable property. Yet, almost all fast convergence guarantees in learning in games require prior knowledge of the utility scale. To address this, we develop learning dynamics that achieve fast convergence while being both scale-free, requiring no prior information about utilities, and scale-invariant, remaining unchanged under positive rescaling of utilities. For two-player zero-sum games, we obtain scale-free and scale-invariant dynamics with external regret bounded by $\tilde{O}(A_{\mathrm{diff}})$, where $A_{\mathrm{diff}}$ is the payoff range, which implies an $\tilde{O}(A_{\mathrm{diff}} / T)$ convergence rate to Nash equilibrium after $T$ rounds. For multiplayer general-sum games with $n$ players and $m$ actions, we obtain scale-free and scale-invariant dynamics with swap regret bounded by $O(U_{\mathrm{max}} \log T)$, where $U_{\mathrm{max}}$ is the range of the utilities, ignoring the dependence on the number of players and actions. This yields an $O(U_{\mathrm{max}} \log T / T)$ convergence rate to correlated equilibrium. Our learning dynamics are based on optimistic follow-the-regularized-leader with an adaptive learning rate that incorporates the squared path length of the opponents' gradient vectors, together with a new stopping-time analysis that exploits negative terms in regret bounds without scale-dependent tuning. For general-sum games, scale-free learning is enabled also by a technique called doubling clipping, which clips observed gradients based on past observations.

Adversarial Learning in Games with Bandit Feedback: Logarithmic Pure-Strategy Maximin Regret

Learning to play zero-sum games is a fundamental problem in game theory and machine learning. While significant progress has been made in minimizing external regret in the self-play settings or with full-information feedback, real-world applications often force learners to play against unknown, arbitrary opponents and restrict learners to bandit feedback where only the payoff of the realized action is observable. In such challenging settings, it is well-known that $Ω(\sqrt{T})$ external regret is unavoidable (where T is the number of rounds). To overcome this barrier, we investigate adversarial learning in zero-sum games under bandit feedback, aiming to minimize the deficit against the maximin pure strategy -- a metric we term Pure-Strategy Maximin Regret. We analyze this problem under two bandit feedback models: uninformed (only the realized reward is revealed) and informed (both the reward and the opponent's action are revealed). For uninformed bandit learning of normal-form games, we show that the Tsallis-INF algorithm achieves $O(c \log T)$ instance-dependent regret with a game-dependent parameter $c$. Crucially, we prove an information-theoretic lower bound showing that the dependence on c is necessary. To overcome this hardness, we turn to the informed setting and introduce Maximin-UCB, which obtains another regret bound of the form $O(c' \log T)$ for a different game-dependent parameter $c'$ that could potentially be much smaller than $c$. Finally, we generalize both results to bilinear games over an arbitrary, large action set, proposing Tsallis-FTRL-SPM and Maximin-LinUCB for the uninformed and informed setting respectively and establishing similar game-dependent logarithmic regret bounds.

Fast EXP3 Algorithms

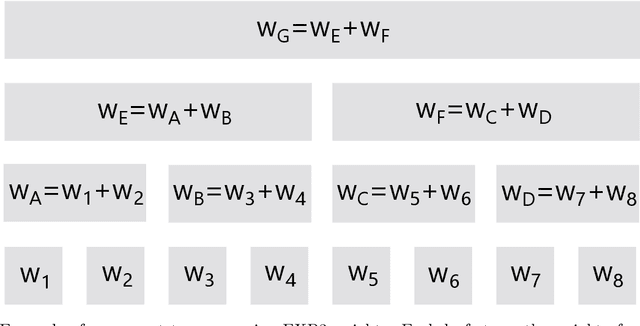
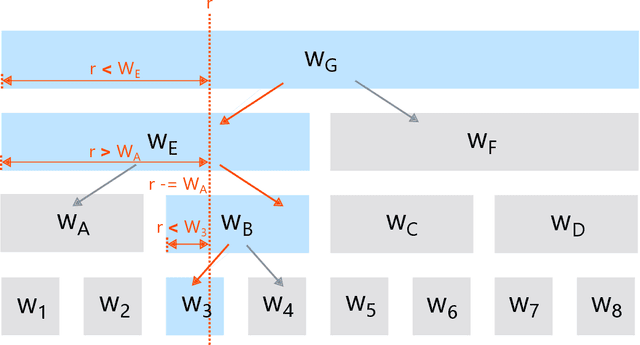
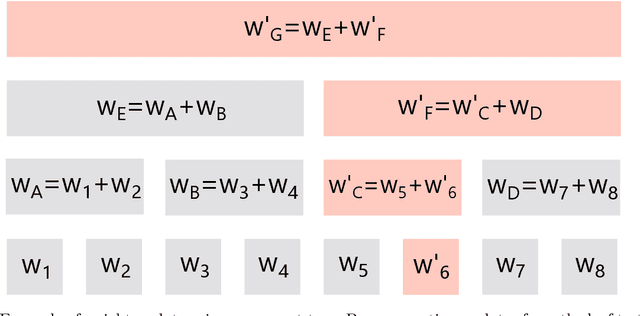
We point out that EXP3 can be implemented in constant time per round, propose more practical algorithms, and analyze the trade-offs between the regret bounds and time complexities of these algorithms.

Reinforcement Learning from Adversarial Preferences in Tabular MDPs

We introduce a new framework of episodic tabular Markov decision processes (MDPs) with adversarial preferences, which we refer to as preference-based MDPs (PbMDPs). Unlike standard episodic MDPs with adversarial losses, where the numerical value of the loss is directly observed, in PbMDPs the learner instead observes preferences between two candidate arms, which represent the choices being compared. In this work, we focus specifically on the setting where the reward functions are determined by Borda scores. We begin by establishing a regret lower bound for PbMDPs with Borda scores. As a preliminary step, we present a simple instance to prove a lower bound of $\Omega(\sqrt{HSAT})$ for episodic MDPs with adversarial losses, where $H$ is the number of steps per episode, $S$ is the number of states, $A$ is the number of actions, and $T$ is the number of episodes. Leveraging this construction, we then derive a regret lower bound of $\Omega( (H^2 S K)^{1/3} T^{2/3} )$ for PbMDPs with Borda scores, where $K$ is the number of arms. Next, we develop algorithms that achieve a regret bound of order $T^{2/3}$. We first propose a global optimization approach based on online linear optimization over the set of all occupancy measures, achieving a regret bound of $\tilde{O}((H^2 S^2 K)^{1/3} T^{2/3} )$ under known transitions. However, this approach suffers from suboptimal dependence on the potentially large number of states $S$ and computational inefficiency. To address this, we propose a policy optimization algorithm whose regret is roughly bounded by $\tilde{O}( (H^6 S K^5)^{1/3} T^{2/3} )$ under known transitions, and further extend the result to the unknown-transition setting.

Bandit Max-Min Fair Allocation

In this paper, we study a new decision-making problem called the bandit max-min fair allocation (BMMFA) problem. The goal of this problem is to maximize the minimum utility among agents with additive valuations by repeatedly assigning indivisible goods to them. One key feature of this problem is that each agent's valuation for each item can only be observed through the semi-bandit feedback, while existing work supposes that the item values are provided at the beginning of each round. Another key feature is that the algorithm's reward function is not additive with respect to rounds, unlike most bandit-setting problems. Our first contribution is to propose an algorithm that has an asymptotic regret bound of $O(m\sqrt{T}\ln T/n + m\sqrt{T \ln(mnT)})$, where $n$ is the number of agents, $m$ is the number of items, and $T$ is the time horizon. This is based on a novel combination of bandit techniques and a resource allocation algorithm studied in the literature on competitive analysis. Our second contribution is to provide the regret lower bound of $\Omega(m\sqrt{T}/n)$. When $T$ is sufficiently larger than $n$, the gap between the upper and lower bounds is a logarithmic factor of $T$.

Optimal Regret of Bernoulli Bandits under Global Differential Privacy

As sequential learning algorithms are increasingly applied to real life, ensuring data privacy while maintaining their utilities emerges as a timely question. In this context, regret minimisation in stochastic bandits under $\epsilon$-global Differential Privacy (DP) has been widely studied. Unlike bandits without DP, there is a significant gap between the best-known regret lower and upper bound in this setting, though they "match" in order. Thus, we revisit the regret lower and upper bounds of $\epsilon$-global DP algorithms for Bernoulli bandits and improve both. First, we prove a tighter regret lower bound involving a novel information-theoretic quantity characterising the hardness of $\epsilon$-global DP in stochastic bandits. Our lower bound strictly improves on the existing ones across all $\epsilon$ values. Then, we choose two asymptotically optimal bandit algorithms, i.e. DP-KLUCB and DP-IMED, and propose their DP versions using a unified blueprint, i.e., (a) running in arm-dependent phases, and (b) adding Laplace noise to achieve privacy. For Bernoulli bandits, we analyse the regrets of these algorithms and show that their regrets asymptotically match our lower bound up to a constant arbitrary close to 1. This refutes the conjecture that forgetting past rewards is necessary to design optimal bandit algorithms under global DP. At the core of our algorithms lies a new concentration inequality for sums of Bernoulli variables under Laplace mechanism, which is a new DP version of the Chernoff bound. This result is universally useful as the DP literature commonly treats the concentrations of Laplace noise and random variables separately, while we couple them to yield a tighter bound.

Influential Bandits: Pulling an Arm May Change the Environment

While classical formulations of multi-armed bandit problems assume that each arm's reward is independent and stationary, real-world applications often involve non-stationary environments and interdependencies between arms. In particular, selecting one arm may influence the future rewards of other arms, a scenario not adequately captured by existing models such as rotting bandits or restless bandits. To address this limitation, we propose the influential bandit problem, which models inter-arm interactions through an unknown, symmetric, positive semi-definite interaction matrix that governs the dynamics of arm losses. We formally define this problem and establish two regret lower bounds, including a superlinear $\Omega(T^2 / \log^2 T)$ bound for the standard UCB algorithm and an algorithm-independent $\Omega(T)$ bound, which highlight the inherent difficulty of the setting. We then introduce a new algorithm based on a lower confidence bound (LCB) estimator tailored to the structure of the loss dynamics. Under mild assumptions, our algorithm achieves a regret of $O(KT \log T)$, which is nearly optimal in terms of its dependence on the time horizon. The algorithm is simple to implement and computationally efficient. Empirical evaluations on both synthetic and real-world datasets demonstrate the presence of inter-arm influence and confirm the superior performance of our method compared to conventional bandit algorithms.

Instance-Dependent Regret Bounds for Learning Two-Player Zero-Sum Games with Bandit Feedback

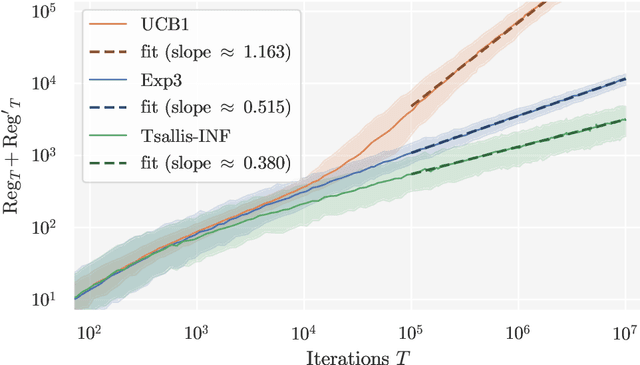
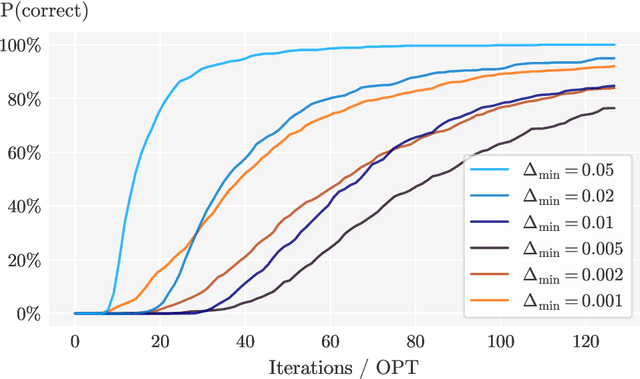
No-regret self-play learning dynamics have become one of the premier ways to solve large-scale games in practice. Accelerating their convergence via improving the regret of the players over the naive $O(\sqrt{T})$ bound after $T$ rounds has been extensively studied in recent years, but almost all studies assume access to exact gradient feedback. We address the question of whether acceleration is possible under bandit feedback only and provide an affirmative answer for two-player zero-sum normal-form games. Specifically, we show that if both players apply the Tsallis-INF algorithm of Zimmert and Seldin (2018, arXiv:1807.07623), then their regret is at most $O(c_1 \log T + \sqrt{c_2 T})$, where $c_1$ and $c_2$ are game-dependent constants that characterize the difficulty of learning -- $c_1$ resembles the complexity of learning a stochastic multi-armed bandit instance and depends inversely on some gap measures, while $c_2$ can be much smaller than the number of actions when the Nash equilibria have a small support or are close to the boundary. In particular, for the case when a pure strategy Nash equilibrium exists, $c_2$ becomes zero, leading to an optimal instance-dependent regret bound as we show. We additionally prove that in this case, our algorithm also enjoys last-iterate convergence and can identify the pure strategy Nash equilibrium with near-optimal sample complexity.

Data-dependent Bounds with $T$-Optimal Best-of-Both-Worlds Guarantees in Multi-Armed Bandits using Stability-Penalty Matching

Existing data-dependent and best-of-both-worlds regret bounds for multi-armed bandits problems have limited adaptivity as they are either data-dependent but not best-of-both-worlds (BOBW), BOBW but not data-dependent or have sub-optimal $O(\sqrt{T\ln{T}})$ worst-case guarantee in the adversarial regime. To overcome these limitations, we propose real-time stability-penalty matching (SPM), a new method for obtaining regret bounds that are simultaneously data-dependent, best-of-both-worlds and $T$-optimal for multi-armed bandits problems. In particular, we show that real-time SPM obtains bounds with worst-case guarantees of order $O(\sqrt{T})$ in the adversarial regime and $O(\ln{T})$ in the stochastic regime while simultaneously being adaptive to data-dependent quantities such as sparsity, variations, and small losses. Our results are obtained by extending the SPM technique for tuning the learning rates in the follow-the-regularized-leader (FTRL) framework, which further indicates that the combination of SPM and FTRL is a promising approach for proving new adaptive bounds in online learning problems.

Corrupted Learning Dynamics in Games

Learning in games is the problem where multiple players interact in a shared environment, each aiming to minimize their own regret, and it is known that an approximate equilibrium can be obtained when all players employ no-regret algorithms. Notably, by adopting optimistic follow-the-regularized-leader (OFTRL), the regret of each player after $T$ rounds is constant in two-player zero-sum games, implying that an equilibrium can be computed at a faster rate of $O(1/T)$. However, this acceleration is limited to the honest regime, where all players fully adhere to the given algorithms. To address this limitation, this paper presents corrupted learning dynamics that adaptively find an equilibrium at a rate dependent on the degree of deviation by each player from the given algorithm's output. First, in two-player zero-sum games, we provide learning dynamics where the external regret of the x-player (and similarly for the y-player) in the corrupted regime is roughly bounded by $O(\log (m_\mathrm{x} m_\mathrm{y}) + \sqrt{C_\mathrm{y}} + C_\mathrm{x})$, which implies a convergence rate of $\tilde{O}((\sqrt{C_\mathrm{y}} + C_\mathrm{x})/T)$ to a Nash equilibrium. Here, $m_\mathrm{x}$ and $m_\mathrm{y}$ are the number of actions of the x- and y-players, respectively, and $C_\mathrm{x}$ and $C_\mathrm{y}$ are the cumulative deviations of the x- and y-players from their given algorithms. Furthermore, we extend our approach to multi-player general-sum games, showing that the swap regret of player $i$ in the corrupted regime is bounded by $O(\log T + \sqrt{\sum_j C_j \log T} + C_i)$, where $C_i$ is the cumulative deviations of player $i$ from the given algorithm. This implies a convergence rate of $O((\log T + \sqrt{\sum_j C_j \log T} + C_i)/T)$ to a correlated equilibrium. Our learning dynamics are agnostic to the corruption levels and are based on OFTRL with new adaptive learning rates.