Online Fair Division with Contextual Bandits

This paper considers a novel online fair division problem involving multiple agents in which a learner observes an indivisible item that has to be irrevocably allocated to one of the agents while satisfying a fairness and efficiency constraint. Existing algorithms assume a small number of items with a sufficiently large number of copies, which ensures a good utility estimation for all item-agent pairs. However, such an assumption may not hold in many real-life applications, e.g., an online platform that has a large number of users (items) who only use the platform's service providers (agents) a few times (a few copies of items), which makes it difficult to estimate the utility for all item-agent pairs. To overcome this challenge, we model the online fair division problem using contextual bandits, assuming the utility is an unknown function of the item-agent features. We then propose algorithms for online fair division with sub-linear regret guarantees. Our experimental results also verify the different performance aspects of the proposed algorithms.

Solving a Stackelberg Game on Transportation Networks in a Dynamic Crime Scenario: A Mixed Approach on Multi-Layer Networks

Interdicting a criminal with limited police resources is a challenging task as the criminal changes location over time. The size of the large transportation network further adds to the difficulty of this scenario. To tackle this issue, we consider the concept of a layered graph. At each time stamp, we create a copy of the entire transportation network to track the possible movements of both players, the attacker and the defenders. We consider a Stackelberg game in a dynamic crime scenario where the attacker changes location over time while the defenders attempt to interdict the attacker on his escape route. Given a set of defender strategies, the optimal attacker strategy is determined by applying Dijkstra's algorithm on the layered networks. Here, the attacker aims to minimize while the defenders aim to maximize the probability of interdiction. We develop an approximation algorithm on the layered networks to find near-optimal strategy for defenders. The efficacy of the developed approach is compared with the adopted MILP approach. We compare the results in terms of computational time and solution quality. The quality of the results demonstrates the need for the developed approach, as it effectively solves the complex problem within a short amount of time.

Online $\mathrm{L}^{ atural}$-Convex Minimization

An online decision-making problem is a learning problem in which a player repeatedly makes decisions in order to minimize the long-term loss. These problems that emerge in applications often have nonlinear combinatorial objective functions, and developing algorithms for such problems has attracted considerable attention. An existing general framework for dealing with such objective functions is the online submodular minimization. However, practical problems are often out of the scope of this framework, since the domain of a submodular function is limited to a subset of the unit hypercube. To manage this limitation of the existing framework, we in this paper introduce the online $\mathrm{L}^{\natural}$-convex minimization, where an $\mathrm{L}^{\natural}$-convex function generalizes a submodular function so that the domain is a subset of the integer lattice. We propose computationally efficient algorithms for the online $\mathrm{L}^{\natural}$-convex function minimization in two major settings: the full information and the bandit settings. We analyze the regrets of these algorithms and show in particular that our algorithm for the full information setting obtains a tight regret bound up to a constant factor. We also demonstrate several motivating examples that illustrate the usefulness of the online $\mathrm{L}^{\natural}$-convex minimization.

Diffusion and Auction on Graphs

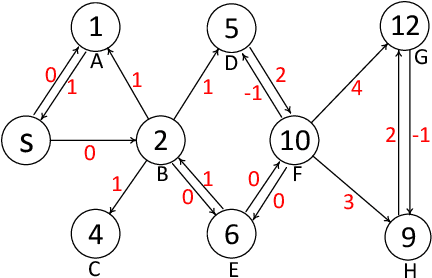
Auction is the common paradigm for resource allocation which is a fundamental problem in human society. Existing research indicates that the two primary objectives, the seller's revenue and the allocation efficiency, are generally conflicting in auction design. For the first time, we expand the domain of the classic auction to a social graph and formally identify a new class of auction mechanisms on graphs. All mechanisms in this class are incentive-compatible and also promote all buyers to diffuse the auction information to others, whereby both the seller's revenue and the allocation efficiency are significantly improved comparing with the Vickrey auction. It is found that the recently proposed information diffusion mechanism is an extreme case with the lowest revenue in this new class. Our work could potentially inspire a new perspective for the efficient and optimal auction design and could be applied into the prevalent online social and economic networks.

Distributed Constraint Problems for Utilitarian Agents with Privacy Concerns, Recast as POMDPs

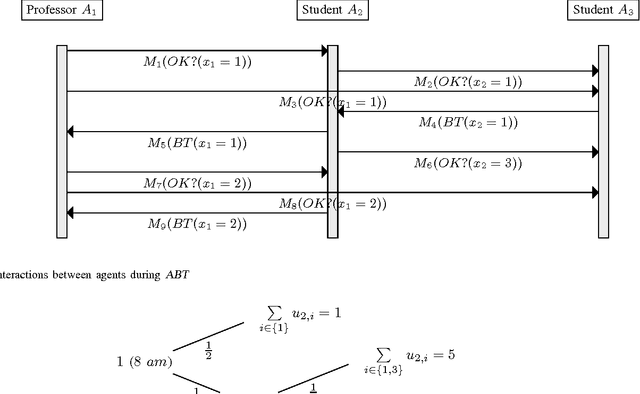
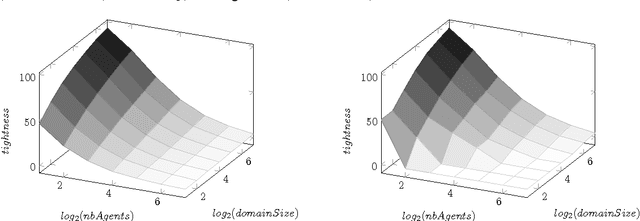
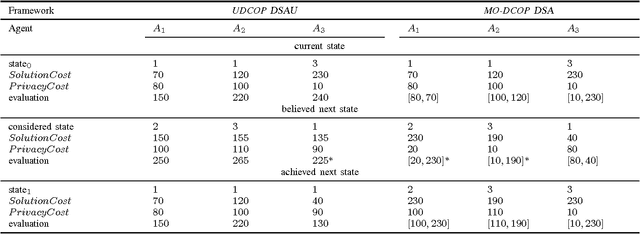
Privacy has traditionally been a major motivation for distributed problem solving. Distributed Constraint Satisfaction Problem (DisCSP) as well as Distributed Constraint Optimization Problem (DCOP) are fundamental models used to solve various families of distributed problems. Even though several approaches have been proposed to quantify and preserve privacy in such problems, none of them is exempt from limitations. Here we approach the problem by assuming that computation is performed among utilitarian agents. We introduce a utilitarian approach where the utility of each state is estimated as the difference between the reward for reaching an agreement on assignments of shared variables and the cost of privacy loss. We investigate extensions to solvers where agents integrate the utility function to guide their search and decide which action to perform, defining thereby their policy. We show that these extended solvers succeed in significantly reducing privacy loss without significant degradation of the solution quality.

DisCSPs with Privacy Recast as Planning Problems for Utility-based Agents

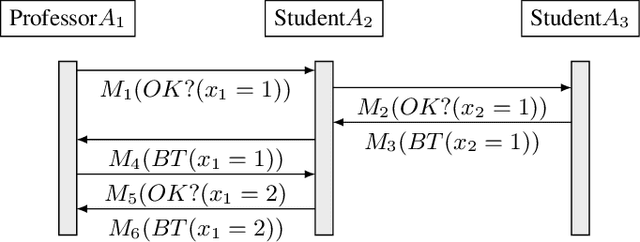
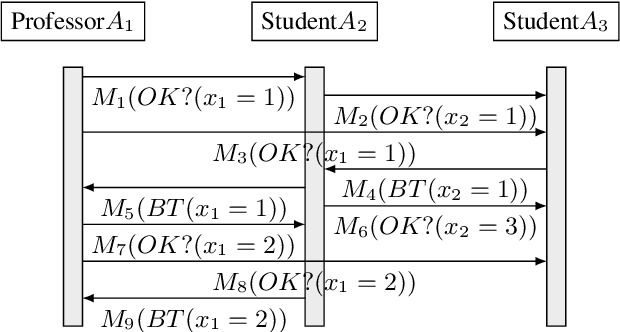
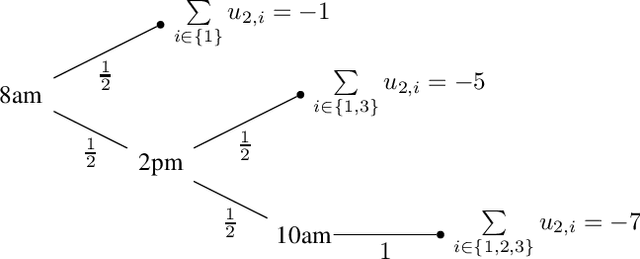
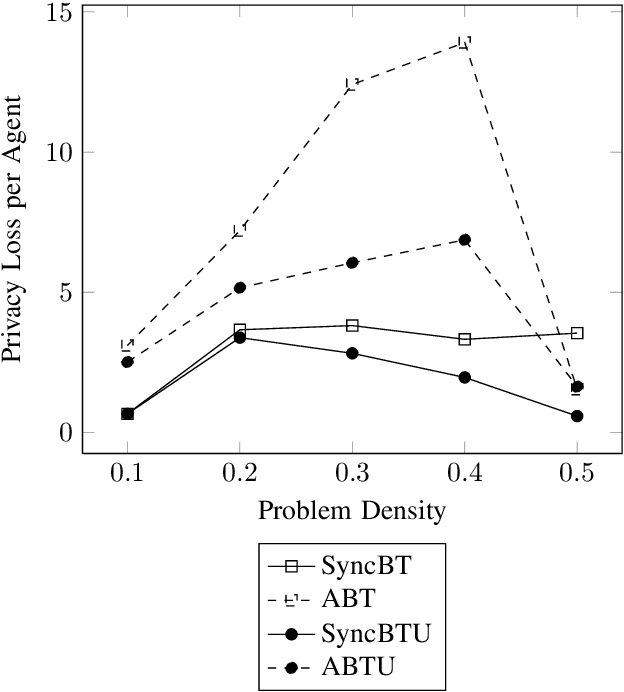
Privacy has traditionally been a major motivation for decentralized problem solving. However, even though several metrics have been proposed to quantify it, none of them is easily integrated with common solvers. Constraint programming is a fundamental paradigm used to approach various families of problems. We introduce Utilitarian Distributed Constraint Satisfaction Problems (UDisCSP) where the utility of each state is estimated as the difference between the the expected rewards for agreements on assignments for shared variables, and the expected cost of privacy loss. Therefore, a traditional DisCSP with privacy requirements is viewed as a planning problem. The actions available to agents are: communication and local inference. Common decentralized solvers are evaluated here from the point of view of their interpretation as greedy planners. Further, we investigate some simple extensions where these solvers start taking into account the utility function. In these extensions we assume that the planning problem is further restricting the set of communication actions to only the communication primitives present in the corresponding solver protocols. The solvers obtained for the new type of problems propose the action (communication/inference) to be performed in each situation, defining thereby the policy.

Utilitarian Distributed Constraint Optimization Problems

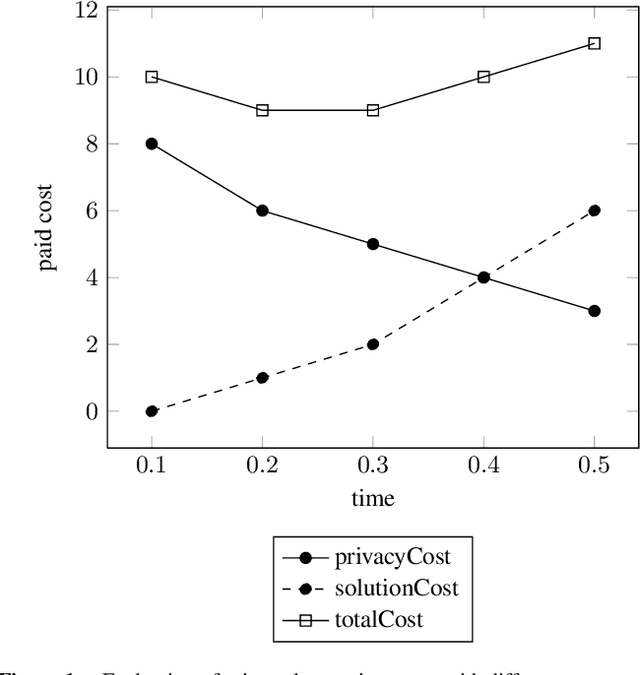
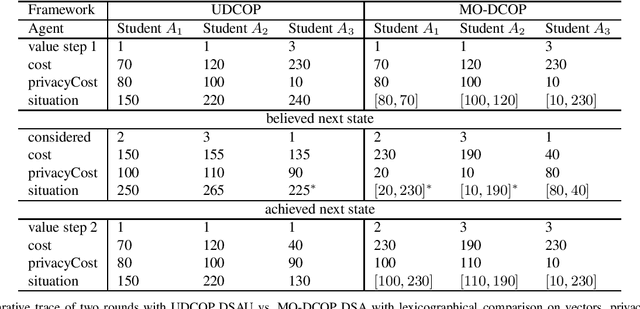
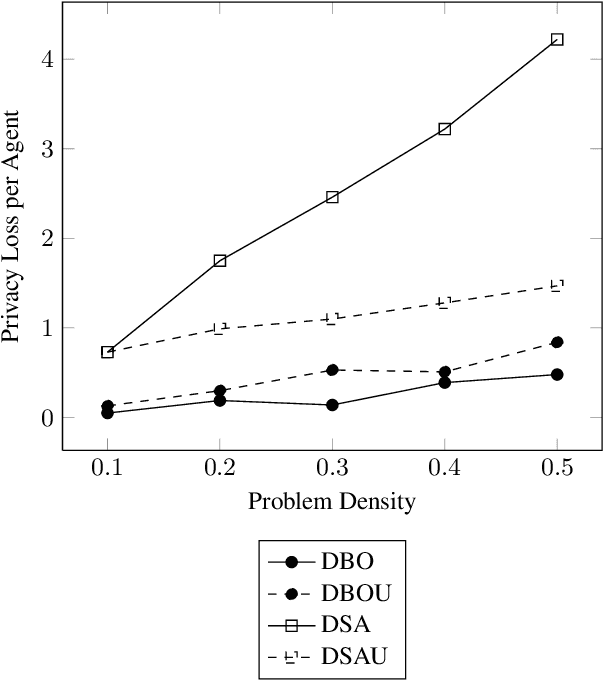
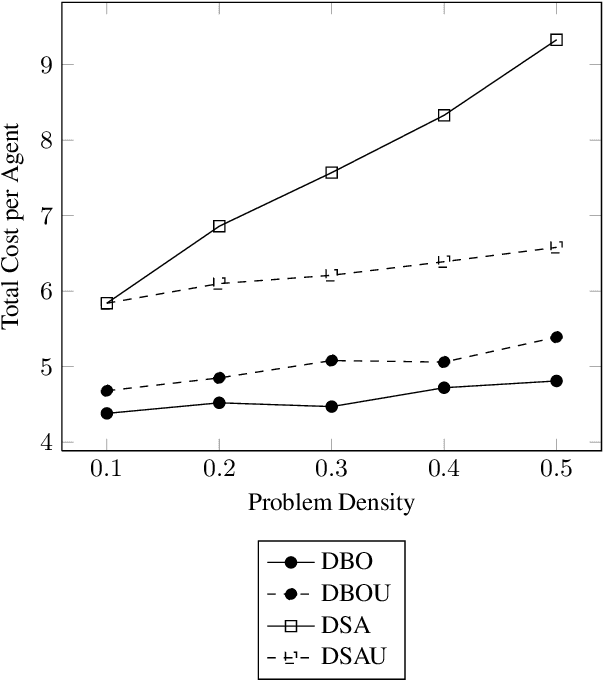
Privacy has been a major motivation for distributed problem optimization. However, even though several methods have been proposed to evaluate it, none of them is widely used. The Distributed Constraint Optimization Problem (DCOP) is a fundamental model used to approach various families of distributed problems. As privacy loss does not occur when a solution is accepted, but when it is proposed, privacy requirements cannot be interpreted as a criteria of the objective function of the DCOP. Here we approach the problem by letting both the optimized costs found in DCOPs and the privacy requirements guide the agents' exploration of the search space. We introduce Utilitarian Distributed Constraint Optimization Problem (UDCOP) where the costs and the privacy requirements are used as parameters to a heuristic modifying the search process. Common stochastic algorithms for decentralized constraint optimization problems are evaluated here according to how well they preserve privacy. Further, we propose some extensions where these solvers modify their search process to take into account their privacy requirements, succeeding in significantly reducing their privacy loss without significant degradation of the solution quality.