Online $\mathrm{L}^{ atural}$-Convex Minimization

An online decision-making problem is a learning problem in which a player repeatedly makes decisions in order to minimize the long-term loss. These problems that emerge in applications often have nonlinear combinatorial objective functions, and developing algorithms for such problems has attracted considerable attention. An existing general framework for dealing with such objective functions is the online submodular minimization. However, practical problems are often out of the scope of this framework, since the domain of a submodular function is limited to a subset of the unit hypercube. To manage this limitation of the existing framework, we in this paper introduce the online $\mathrm{L}^{\natural}$-convex minimization, where an $\mathrm{L}^{\natural}$-convex function generalizes a submodular function so that the domain is a subset of the integer lattice. We propose computationally efficient algorithms for the online $\mathrm{L}^{\natural}$-convex function minimization in two major settings: the full information and the bandit settings. We analyze the regrets of these algorithms and show in particular that our algorithm for the full information setting obtains a tight regret bound up to a constant factor. We also demonstrate several motivating examples that illustrate the usefulness of the online $\mathrm{L}^{\natural}$-convex minimization.

Computational Complexity of Normalizing Constants for the Product of Determinantal Point Processes

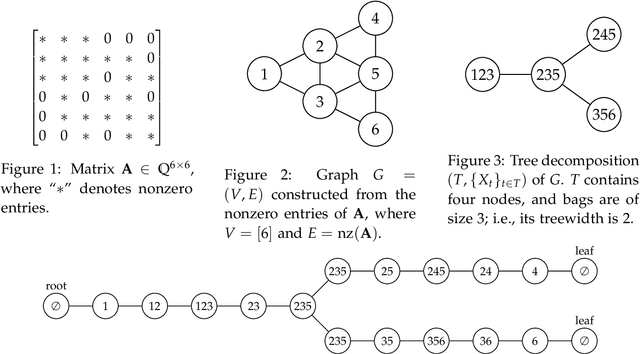
We consider the product of determinantal point processes (DPPs), a point process whose probability mass is proportional to the product of principal minors of multiple matrices, as a natural, promising generalization of DPPs. We study the computational complexity of computing its normalizing constant, which is among the most essential probabilistic inference tasks. Our complexity-theoretic results (almost) rule out the existence of efficient algorithms for this task unless the input matrices are forced to have favorable structures. In particular, we prove the following: (1) Computing $\sum_S\det({\bf A}_{S,S})^p$ exactly for every (fixed) positive even integer $p$ is UP-hard and Mod$_3$P-hard, which gives a negative answer to an open question posed by Kulesza and Taskar. (2) $\sum_S\det({\bf A}_{S,S})\det({\bf B}_{S,S})\det({\bf C}_{S,S})$ is NP-hard to approximate within a factor of $2^{O(|I|^{1-\epsilon})}$ or $2^{O(n^{1/\epsilon})}$ for any $\epsilon>0$, where $|I|$ is the input size and $n$ is the order of the input matrix. This result is stronger than the #P-hardness for the case of two matrices derived by Gillenwater. (3) There exists a $k^{O(k)}n^{O(1)}$-time algorithm for computing $\sum_S\det({\bf A}_{S,S})\det({\bf B}_{S,S})$, where $k$ is the maximum rank of $\bf A$ and $\bf B$ or the treewidth of the graph formed by nonzero entries of $\bf A$ and $\bf B$. Such parameterized algorithms are said to be fixed-parameter tractable. These results can be extended to the fixed-size case. Further, we present two applications of fixed-parameter tractable algorithms given a matrix $\bf A$ of treewidth $w$: (4) We can compute a $2^{\frac{n}{2p-1}}$-approximation to $\sum_S\det({\bf A}_{S,S})^p$ for any fractional number $p>1$ in $w^{O(wp)}n^{O(1)}$ time. (5) We can find a $2^{\sqrt n}$-approximation to unconstrained MAP inference in $w^{O(w\sqrt n)}n^{O(1)}$ time.

Spanning Tree Constrained Determinantal Point Processes are Hard to (Approximately) Evaluate

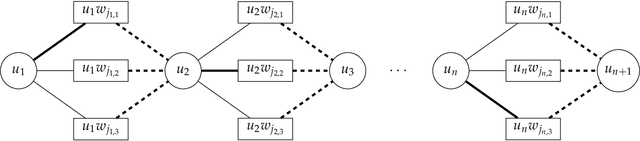
We consider determinantal point processes (DPPs) constrained by spanning trees. Given a graph $G=(V,E)$ and a positive semi-definite matrix $\mathbf{A}$ indexed by $E$, a spanning-tree DPP defines a distribution such that we draw $S\subseteq E$ with probability proportional to $\det(\mathbf{A}_S)$ only if $S$ induces a spanning tree. We prove $\sharp\textsf{P}$-hardness of computing the normalizing constant for spanning-tree DPPs and provide an approximation-preserving reduction from the mixed discriminant, for which FPRAS is not known. We show similar results for DPPs constrained by forests.