COBRA: Contextual Bandit Algorithm for Ensuring Truthful Strategic Agents

This paper considers a contextual bandit problem involving multiple agents, where a learner sequentially observes the contexts and the agent's reported arms, and then selects the arm that maximizes the system's overall reward. Existing work in contextual bandits assumes that agents truthfully report their arms, which is unrealistic in many real-life applications. For instance, consider an online platform with multiple sellers; some sellers may misrepresent product quality to gain an advantage, such as having the platform preferentially recommend their products to online users. To address this challenge, we propose an algorithm, COBRA, for contextual bandit problems involving strategic agents that disincentivize their strategic behavior without using any monetary incentives, while having incentive compatibility and a sub-linear regret guarantee. Our experimental results also validate the different performance aspects of our proposed algorithm.

ActiveDPO: Active Direct Preference Optimization for Sample-Efficient Alignment

The recent success of using human preferences to align large language models (LLMs) has significantly improved their performance in various downstream tasks like question answering, mathematical reasoning, and code generation. However,3 achieving effective LLM alignment depends on high-quality human preference datasets. Collecting these datasets requires human preference annotation, which is costly and resource-intensive, necessitating efficient active data selection methods. Existing methods either lack a strong theoretical foundation or depend on restrictive reward function assumptions (e.g., linearity). To this end, we propose an algorithm, ActiveDPO, that uses a theoretically grounded data selection criterion for non-linear reward functions while directly leveraging the LLM itself to parameterize the reward model that is used for active data selection. As a result, ActiveDPO explicitly accounts for the influence of LLM on data selection, unlike methods that select the data without considering the LLM that is being aligned, thereby leading to more effective and efficient data collection. Extensive experiments show that ActiveDPO outperforms existing methods across various models and datasets.

Active Human Feedback Collection via Neural Contextual Dueling Bandits

Collecting human preference feedback is often expensive, leading recent works to develop principled algorithms to select them more efficiently. However, these works assume that the underlying reward function is linear, an assumption that does not hold in many real-life applications, such as online recommendation and LLM alignment. To address this limitation, we propose Neural-ADB, an algorithm based on the neural contextual dueling bandit framework that provides a principled and practical method for collecting human preference feedback when the underlying latent reward function is non-linear. We theoretically show that when preference feedback follows the Bradley-Terry-Luce model, the worst sub-optimality gap of the policy learned by Neural-ADB decreases at a sub-linear rate as the preference dataset increases. Our experimental results on problem instances derived from synthetic preference datasets further validate the effectiveness of Neural-ADB.

TETRIS: Optimal Draft Token Selection for Batch Speculative Decoding

We propose TETRIS, a novel method that optimizes the total throughput of batch speculative decoding in multi-request settings. Unlike existing methods that optimize for a single request or a group of requests as a whole, TETRIS actively selects the most promising draft tokens (for every request in a batch) to be accepted when verified in parallel, resulting in fewer rejected tokens and hence less wasted computing resources. Such an effective resource utilization to achieve fast inference in large language models (LLMs) is especially important to service providers with limited inference capacity. Compared to baseline speculative decoding, TETRIS yields a consistently higher acceptance rate and more effective utilization of the limited inference capacity. We show theoretically and empirically that TETRIS outperforms baseline speculative decoding and existing methods that dynamically select draft tokens, leading to a more efficient batch inference in LLMs.

Online Fair Division with Contextual Bandits

This paper considers a novel online fair division problem involving multiple agents in which a learner observes an indivisible item that has to be irrevocably allocated to one of the agents while satisfying a fairness and efficiency constraint. Existing algorithms assume a small number of items with a sufficiently large number of copies, which ensures a good utility estimation for all item-agent pairs. However, such an assumption may not hold in many real-life applications, e.g., an online platform that has a large number of users (items) who only use the platform's service providers (agents) a few times (a few copies of items), which makes it difficult to estimate the utility for all item-agent pairs. To overcome this challenge, we model the online fair division problem using contextual bandits, assuming the utility is an unknown function of the item-agent features. We then propose algorithms for online fair division with sub-linear regret guarantees. Our experimental results also verify the different performance aspects of the proposed algorithms.

Neural Dueling Bandits

Contextual dueling bandit is used to model the bandit problems, where a learner's goal is to find the best arm for a given context using observed noisy preference feedback over the selected arms for the past contexts. However, existing algorithms assume the reward function is linear, which can be complex and non-linear in many real-life applications like online recommendations or ranking web search results. To overcome this challenge, we use a neural network to estimate the reward function using preference feedback for the previously selected arms. We propose upper confidence bound- and Thompson sampling-based algorithms with sub-linear regret guarantees that efficiently select arms in each round. We then extend our theoretical results to contextual bandit problems with binary feedback, which is in itself a non-trivial contribution. Experimental results on the problem instances derived from synthetic datasets corroborate our theoretical results.

Understanding the Relationship between Prompts and Response Uncertainty in Large Language Models

Large language models (LLMs) are widely used in decision-making, but their reliability, especially in critical tasks like healthcare, is not well-established. Therefore, understanding how LLMs reason and make decisions is crucial for their safe deployment. This paper investigates how the uncertainty of responses generated by LLMs relates to the information provided in the input prompt. Leveraging the insight that LLMs learn to infer latent concepts during pretraining, we propose a prompt-response concept model that explains how LLMs generate responses and helps understand the relationship between prompts and response uncertainty. We show that the uncertainty decreases as the prompt's informativeness increases, similar to epistemic uncertainty. Our detailed experimental results on real datasets validate our proposed model.

Data-Centric AI in the Age of Large Language Models

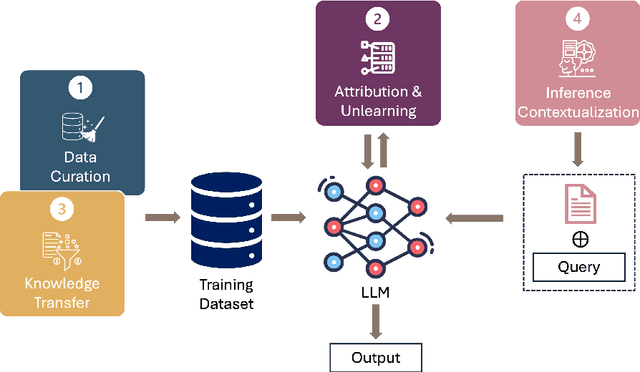
This position paper proposes a data-centric viewpoint of AI research, focusing on large language models (LLMs). We start by making the key observation that data is instrumental in the developmental (e.g., pretraining and fine-tuning) and inferential stages (e.g., in-context learning) of LLMs, and yet it receives disproportionally low attention from the research community. We identify four specific scenarios centered around data, covering data-centric benchmarks and data curation, data attribution, knowledge transfer, and inference contextualization. In each scenario, we underscore the importance of data, highlight promising research directions, and articulate the potential impacts on the research community and, where applicable, the society as a whole. For instance, we advocate for a suite of data-centric benchmarks tailored to the scale and complexity of data for LLMs. These benchmarks can be used to develop new data curation methods and document research efforts and results, which can help promote openness and transparency in AI and LLM research.

Prompt Optimization with Human Feedback

Large language models (LLMs) have demonstrated remarkable performances in various tasks. However, the performance of LLMs heavily depends on the input prompt, which has given rise to a number of recent works on prompt optimization. However, previous works often require the availability of a numeric score to assess the quality of every prompt. Unfortunately, when a human user interacts with a black-box LLM, attaining such a score is often infeasible and unreliable. Instead, it is usually significantly easier and more reliable to obtain preference feedback from a human user, i.e., showing the user the responses generated from a pair of prompts and asking the user which one is preferred. Therefore, in this paper, we study the problem of prompt optimization with human feedback (POHF), in which we aim to optimize the prompt for a black-box LLM using only human preference feedback. Drawing inspiration from dueling bandits, we design a theoretically principled strategy to select a pair of prompts to query for preference feedback in every iteration, and hence introduce our algorithm named automated POHF (APOHF). We apply our APOHF algorithm to various tasks, including optimizing user instructions, prompt optimization for text-to-image generative models, and response optimization with human feedback (i.e., further refining the response using a variant of our APOHF). The results demonstrate that our APOHF can efficiently find a good prompt using a small number of preference feedback instances. Our code can be found at \url{https://github.com/xqlin98/APOHF}.

Exploiting Correlated Auxiliary Feedback in Parameterized Bandits

We study a novel variant of the parameterized bandits problem in which the learner can observe additional auxiliary feedback that is correlated with the observed reward. The auxiliary feedback is readily available in many real-life applications, e.g., an online platform that wants to recommend the best-rated services to its users can observe the user's rating of service (rewards) and collect additional information like service delivery time (auxiliary feedback). In this paper, we first develop a method that exploits auxiliary feedback to build a reward estimator with tight confidence bounds, leading to a smaller regret. We then characterize the regret reduction in terms of the correlation coefficient between reward and its auxiliary feedback. Experimental results in different settings also verify the performance gain achieved by our proposed method.