Distributed Constraint Problems for Utilitarian Agents with Privacy Concerns, Recast as POMDPs

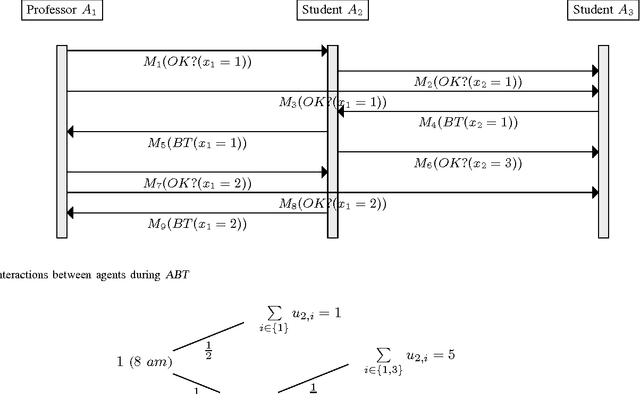
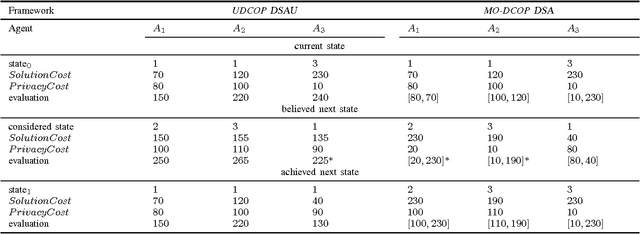
Privacy has traditionally been a major motivation for distributed problem solving. Distributed Constraint Satisfaction Problem (DisCSP) as well as Distributed Constraint Optimization Problem (DCOP) are fundamental models used to solve various families of distributed problems. Even though several approaches have been proposed to quantify and preserve privacy in such problems, none of them is exempt from limitations. Here we approach the problem by assuming that computation is performed among utilitarian agents. We introduce a utilitarian approach where the utility of each state is estimated as the difference between the reward for reaching an agreement on assignments of shared variables and the cost of privacy loss. We investigate extensions to solvers where agents integrate the utility function to guide their search and decide which action to perform, defining thereby their policy. We show that these extended solvers succeed in significantly reducing privacy loss without significant degradation of the solution quality.

DisCSPs with Privacy Recast as Planning Problems for Utility-based Agents

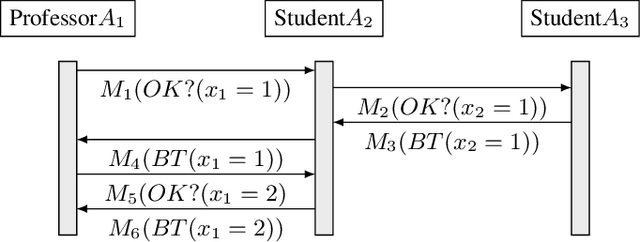
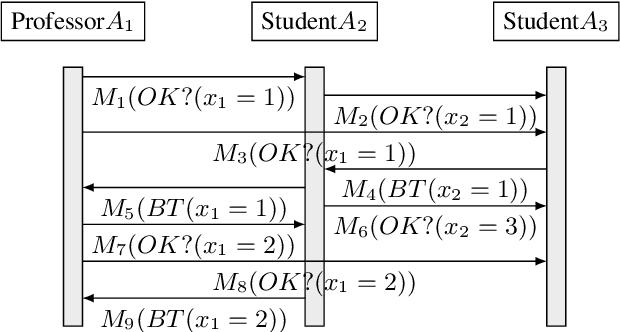
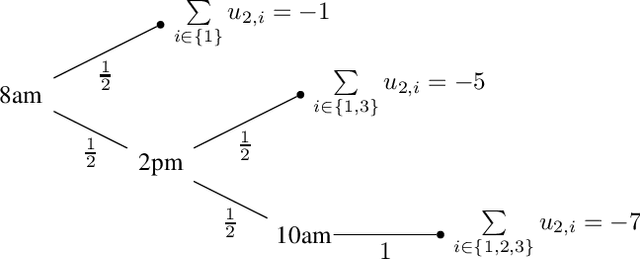
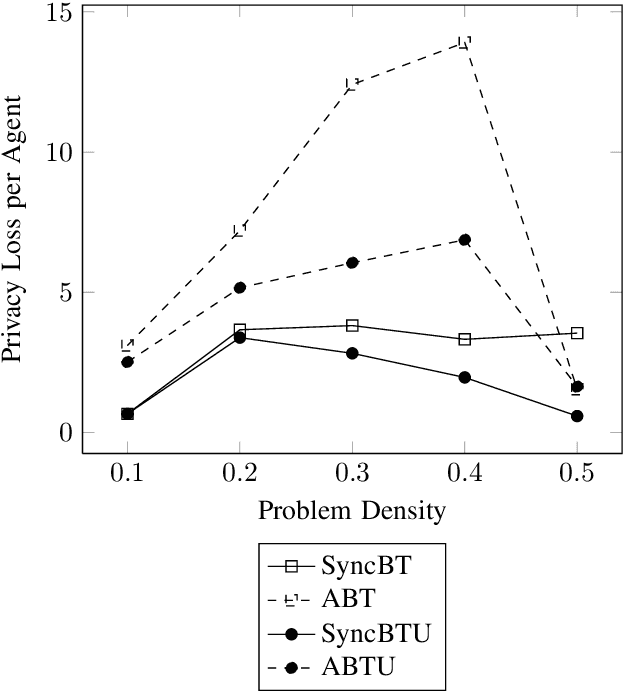
Privacy has traditionally been a major motivation for decentralized problem solving. However, even though several metrics have been proposed to quantify it, none of them is easily integrated with common solvers. Constraint programming is a fundamental paradigm used to approach various families of problems. We introduce Utilitarian Distributed Constraint Satisfaction Problems (UDisCSP) where the utility of each state is estimated as the difference between the the expected rewards for agreements on assignments for shared variables, and the expected cost of privacy loss. Therefore, a traditional DisCSP with privacy requirements is viewed as a planning problem. The actions available to agents are: communication and local inference. Common decentralized solvers are evaluated here from the point of view of their interpretation as greedy planners. Further, we investigate some simple extensions where these solvers start taking into account the utility function. In these extensions we assume that the planning problem is further restricting the set of communication actions to only the communication primitives present in the corresponding solver protocols. The solvers obtained for the new type of problems propose the action (communication/inference) to be performed in each situation, defining thereby the policy.

Utilitarian Distributed Constraint Optimization Problems

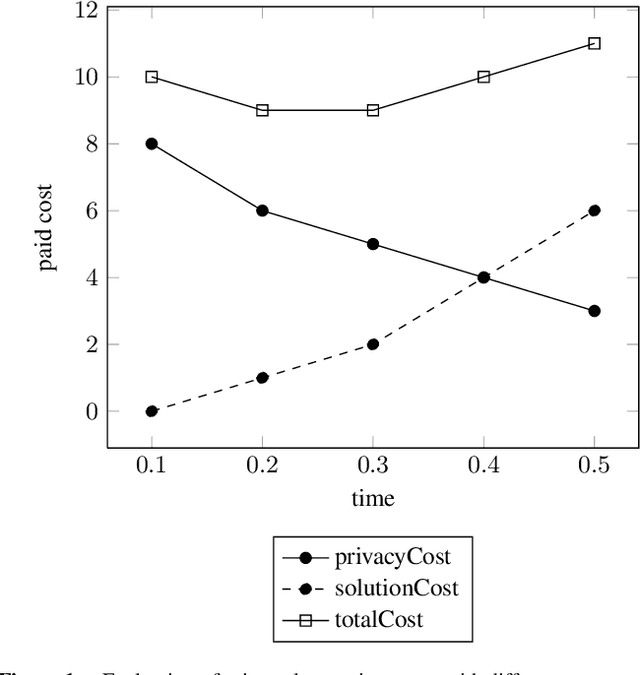
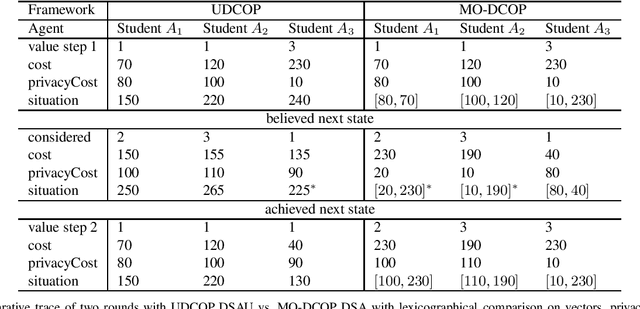
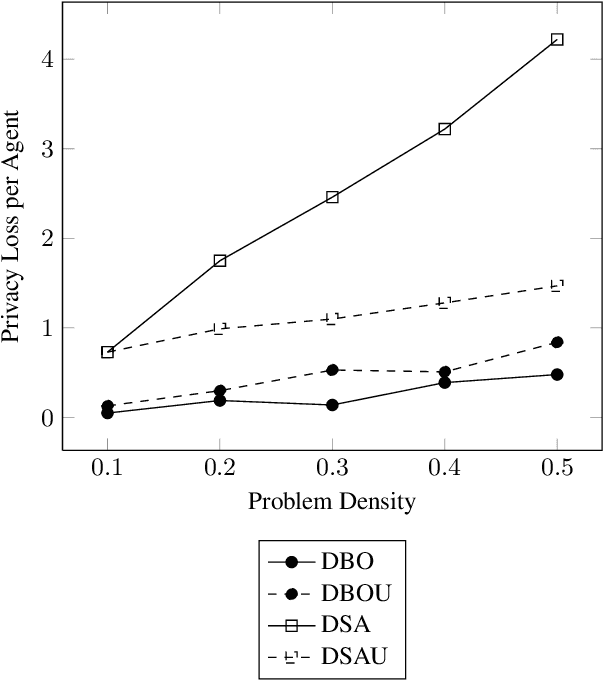
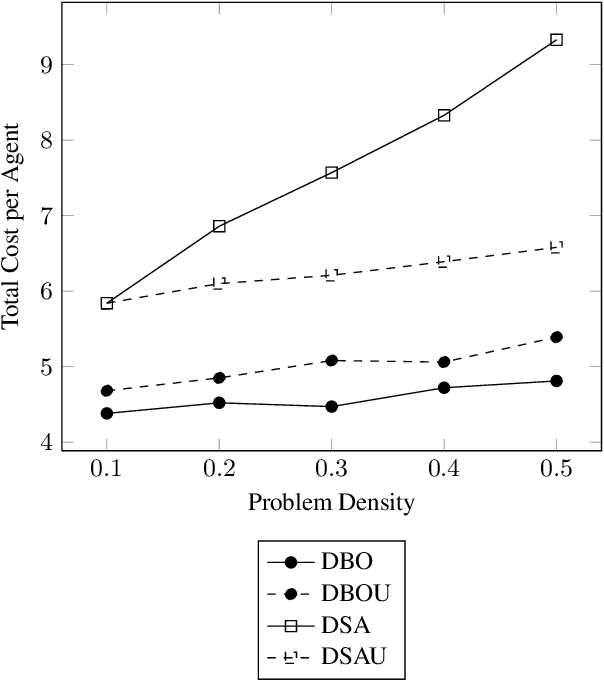
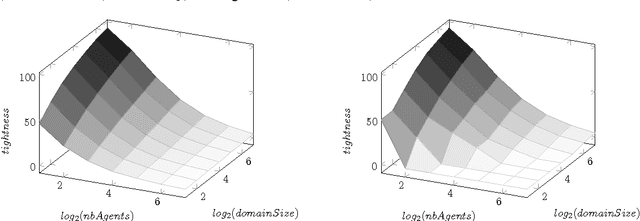
Privacy has been a major motivation for distributed problem optimization. However, even though several methods have been proposed to evaluate it, none of them is widely used. The Distributed Constraint Optimization Problem (DCOP) is a fundamental model used to approach various families of distributed problems. As privacy loss does not occur when a solution is accepted, but when it is proposed, privacy requirements cannot be interpreted as a criteria of the objective function of the DCOP. Here we approach the problem by letting both the optimized costs found in DCOPs and the privacy requirements guide the agents' exploration of the search space. We introduce Utilitarian Distributed Constraint Optimization Problem (UDCOP) where the costs and the privacy requirements are used as parameters to a heuristic modifying the search process. Common stochastic algorithms for decentralized constraint optimization problems are evaluated here according to how well they preserve privacy. Further, we propose some extensions where these solvers modify their search process to take into account their privacy requirements, succeeding in significantly reducing their privacy loss without significant degradation of the solution quality.

Second-Order Consistencies

In this paper, we propose a comprehensive study of second-order consistencies (i.e., consistencies identifying inconsistent pairs of values) for constraint satisfaction. We build a full picture of the relationships existing between four basic second-order consistencies, namely path consistency (PC), 3-consistency (3C), dual consistency (DC) and 2-singleton arc consistency (2SAC), as well as their conservative and strong variants. Interestingly, dual consistency is an original property that can be established by using the outcome of the enforcement of generalized arc consistency (GAC), which makes it rather easy to obtain since constraint solvers typically maintain GAC during search. On binary constraint networks, DC is equivalent to PC, but its restriction to existing constraints, called conservative dual consistency (CDC), is strictly stronger than traditional conservative consistencies derived from path consistency, namely partial path consistency (PPC) and conservative path consistency (CPC). After introducing a general algorithm to enforce strong (C)DC, we present the results of an experimentation over a wide range of benchmarks that demonstrate the interest of (conservative) dual consistency. In particular, we show that enforcing (C)DC before search clearly improves the performance of MAC (the algorithm that maintains GAC during search) on several binary and non-binary structured problems.