DisCSPs with Privacy Recast as Planning Problems for Utility-based Agents
Paper and Code
Apr 22, 2016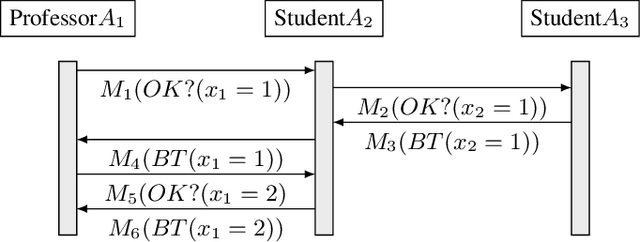
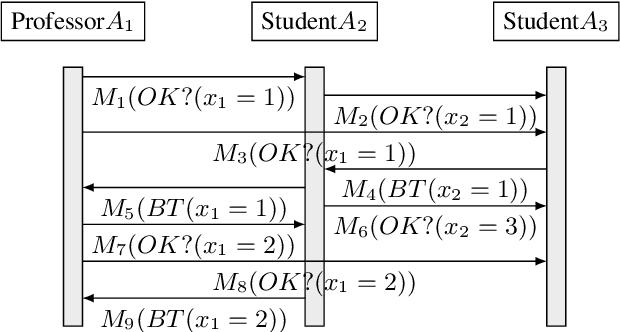
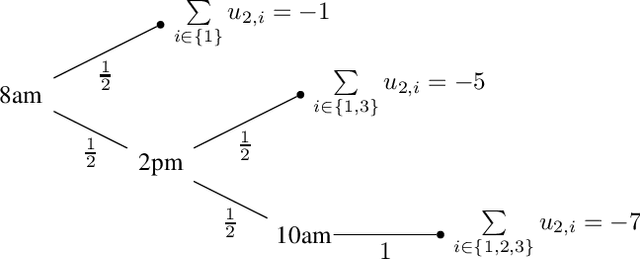
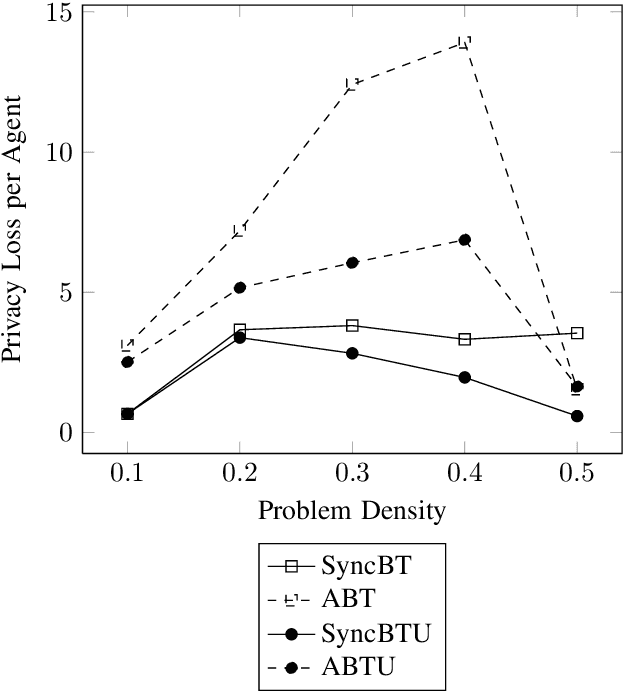
Privacy has traditionally been a major motivation for decentralized problem solving. However, even though several metrics have been proposed to quantify it, none of them is easily integrated with common solvers. Constraint programming is a fundamental paradigm used to approach various families of problems. We introduce Utilitarian Distributed Constraint Satisfaction Problems (UDisCSP) where the utility of each state is estimated as the difference between the the expected rewards for agreements on assignments for shared variables, and the expected cost of privacy loss. Therefore, a traditional DisCSP with privacy requirements is viewed as a planning problem. The actions available to agents are: communication and local inference. Common decentralized solvers are evaluated here from the point of view of their interpretation as greedy planners. Further, we investigate some simple extensions where these solvers start taking into account the utility function. In these extensions we assume that the planning problem is further restricting the set of communication actions to only the communication primitives present in the corresponding solver protocols. The solvers obtained for the new type of problems propose the action (communication/inference) to be performed in each situation, defining thereby the policy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge