No-regret incentive-compatible online learning under exact truthfulness with non-myopic experts

We study an online forecasting setting in which, over $T$ rounds, $N$ strategic experts each report a forecast to a mechanism, the mechanism selects one forecast, and then the outcome is revealed. In any given round, each expert has a belief about the outcome, but the expert wishes to select its report so as to maximize the total number of times it is selected. The goal of the mechanism is to obtain low belief regret: the difference between its cumulative loss (based on its selected forecasts) and the cumulative loss of the best expert in hindsight (as measured by the experts' beliefs). We consider exactly truthful mechanisms for non-myopic experts, meaning that truthfully reporting its belief strictly maximizes the expert's subjective probability of being selected in any future round. Even in the full-information setting, it is an open problem to obtain the first no-regret exactly truthful mechanism in this setting. We develop the first no-regret mechanism for this setting via an online extension of the Independent-Event Lotteries Forecasting Competition Mechanism (I-ELF). By viewing this online I-ELF as a novel instance of Follow the Perturbed Leader (FPL) with noise based on random walks with loss-dependent perturbations, we obtain $\tilde{O}(\sqrt{T N})$ regret. Our results are fueled by new tail bounds for Poisson binomial random variables that we develop. We extend our results to the bandit setting, where we give an exactly truthful mechanism obtaining $\tilde{O}(T^{2/3} N^{1/3})$ regret; this is the first no-regret result even among approximately truthful mechanisms.

Data-dependent Bounds with $T$-Optimal Best-of-Both-Worlds Guarantees in Multi-Armed Bandits using Stability-Penalty Matching

Existing data-dependent and best-of-both-worlds regret bounds for multi-armed bandits problems have limited adaptivity as they are either data-dependent but not best-of-both-worlds (BOBW), BOBW but not data-dependent or have sub-optimal $O(\sqrt{T\ln{T}})$ worst-case guarantee in the adversarial regime. To overcome these limitations, we propose real-time stability-penalty matching (SPM), a new method for obtaining regret bounds that are simultaneously data-dependent, best-of-both-worlds and $T$-optimal for multi-armed bandits problems. In particular, we show that real-time SPM obtains bounds with worst-case guarantees of order $O(\sqrt{T})$ in the adversarial regime and $O(\ln{T})$ in the stochastic regime while simultaneously being adaptive to data-dependent quantities such as sparsity, variations, and small losses. Our results are obtained by extending the SPM technique for tuning the learning rates in the follow-the-regularized-leader (FTRL) framework, which further indicates that the combination of SPM and FTRL is a promising approach for proving new adaptive bounds in online learning problems.

Beyond Minimax Rates in Group Distributionally Robust Optimization via a Novel Notion of Sparsity

The minimax sample complexity of group distributionally robust optimization (GDRO) has been determined up to a $\log(K)$ factor, for $K$ the number of groups. In this work, we venture beyond the minimax perspective via a novel notion of sparsity that we dub $(\lambda, \beta)$-sparsity. In short, this condition means that at any parameter $\theta$, there is a set of at most $\beta$ groups whose risks at $\theta$ all are at least $\lambda$ larger than the risks of the other groups. To find an $\epsilon$-optimal $\theta$, we show via a novel algorithm and analysis that the $\epsilon$-dependent term in the sample complexity can swap a linear dependence on $K$ for a linear dependence on the potentially much smaller $\beta$. This improvement leverages recent progress in sleeping bandits, showing a fundamental connection between the two-player zero-sum game optimization framework for GDRO and per-action regret bounds in sleeping bandits. The aforementioned result assumes having a particular $\lambda$ as input. Perhaps surprisingly, we next show an adaptive algorithm which, up to log factors, gets sample complexity that adapts to the best $(\lambda, \beta)$-sparsity condition that holds. Finally, for a particular input $\lambda$, we also show how to get a dimension-free sample complexity result.

On the price of exact truthfulness in incentive-compatible online learning with bandit feedback: A regret lower bound for WSU-UX

In one view of the classical game of prediction with expert advice with binary outcomes, in each round, each expert maintains an adversarially chosen belief and honestly reports this belief. We consider a recently introduced, strategic variant of this problem with selfish (reputation-seeking) experts, where each expert strategically reports in order to maximize their expected future reputation based on their belief. In this work, our goal is to design an algorithm for the selfish experts problem that is incentive-compatible (IC, or \emph{truthful}), meaning each expert's best strategy is to report truthfully, while also ensuring the algorithm enjoys sublinear regret with respect to the expert with the best belief. Freeman et al. (2020) recently studied this problem in the full information and bandit settings and obtained truthful, no-regret algorithms by leveraging prior work on wagering mechanisms. While their results under full information match the minimax rate for the classical ("honest experts") problem, the best-known regret for their bandit algorithm WSU-UX is $O(T^{2/3})$, which does not match the minimax rate for the classical ("honest bandits") setting. It was unclear whether the higher regret was an artifact of their analysis or a limitation of WSU-UX. We show, via explicit construction of loss sequences, that the algorithm suffers a worst-case $\Omega(T^{2/3})$ lower bound. Left open is the possibility that a different IC algorithm obtains $O(\sqrt{T})$ regret. Yet, WSU-UX was a natural choice for such an algorithm owing to the limited design room for IC algorithms in this setting.

Near-optimal Per-Action Regret Bounds for Sleeping Bandits

We derive near-optimal per-action regret bounds for sleeping bandits, in which both the sets of available arms and their losses in every round are chosen by an adversary. In a setting with $K$ total arms and at most $A$ available arms in each round over $T$ rounds, the best known upper bound is $O(K\sqrt{TA\ln{K}})$, obtained indirectly via minimizing internal sleeping regrets. Compared to the minimax $\Omega(\sqrt{TA})$ lower bound, this upper bound contains an extra multiplicative factor of $K\ln{K}$. We address this gap by directly minimizing the per-action regret using generalized versions of EXP3, EXP3-IX and FTRL with Tsallis entropy, thereby obtaining near-optimal bounds of order $O(\sqrt{TA\ln{K}})$ and $O(\sqrt{T\sqrt{AK}})$. We extend our results to the setting of bandits with advice from sleeping experts, generalizing EXP4 along the way. This leads to new proofs for a number of existing adaptive and tracking regret bounds for standard non-sleeping bandits. Extending our results to the bandit version of experts that report their confidences leads to new bounds for the confidence regret that depends primarily on the sum of experts' confidences. We prove a lower bound, showing that for any minimax optimal algorithms, there exists an action whose regret is sublinear in $T$ but linear in the number of its active rounds.

An improved regret analysis for UCB-N and TS-N

In the setting of stochastic online learning with undirected feedback graphs, Lykouris et al. (2020) previously analyzed the pseudo-regret of the upper confidence bound-based algorithm UCB-N and the Thompson Sampling-based algorithm TS-N. In this note, we show how to improve their pseudo-regret analysis. Our improvement involves refining a key lemma of the previous analysis, allowing a $\log(T)$ factor to be replaced by a factor $\log_2(\alpha) + 3$ for $\alpha$ the independence number of the feedback graph.

Adversarial Online Multi-Task Reinforcement Learning

We consider the adversarial online multi-task reinforcement learning setting, where in each of $K$ episodes the learner is given an unknown task taken from a finite set of $M$ unknown finite-horizon MDP models. The learner's objective is to minimize its regret with respect to the optimal policy for each task. We assume the MDPs in $\mathcal{M}$ are well-separated under a notion of $\lambda$-separability, and show that this notion generalizes many task-separability notions from previous works. We prove a minimax lower bound of $\Omega(K\sqrt{DSAH})$ on the regret of any learning algorithm and an instance-specific lower bound of $\Omega(\frac{K}{\lambda^2})$ in sample complexity for a class of uniformly-good cluster-then-learn algorithms. We use a novel construction called 2-JAO MDP for proving the instance-specific lower bound. The lower bounds are complemented with a polynomial time algorithm that obtains $\tilde{O}(\frac{K}{\lambda^2})$ sample complexity guarantee for the clustering phase and $\tilde{O}(\sqrt{MK})$ regret guarantee for the learning phase, indicating that the dependency on $K$ and $\frac{1}{\lambda^2}$ is tight.

Best-Case Lower Bounds in Online Learning

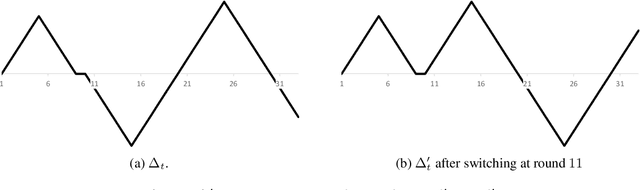
Much of the work in online learning focuses on the study of sublinear upper bounds on the regret. In this work, we initiate the study of best-case lower bounds in online convex optimization, wherein we bound the largest improvement an algorithm can obtain relative to the single best action in hindsight. This problem is motivated by the goal of better understanding the adaptivity of a learning algorithm. Another motivation comes from fairness: it is known that best-case lower bounds are instrumental in obtaining algorithms for decision-theoretic online learning (DTOL) that satisfy a notion of group fairness. Our contributions are a general method to provide best-case lower bounds in Follow The Regularized Leader (FTRL) algorithms with time-varying regularizers, which we use to show that best-case lower bounds are of the same order as existing upper regret bounds: this includes situations with a fixed learning rate, decreasing learning rates, timeless methods, and adaptive gradient methods. In stark contrast, we show that the linearized version of FTRL can attain negative linear regret. Finally, in DTOL with two experts and binary predictions, we fully characterize the best-case sequences, which provides a finer understanding of the best-case lower bounds.

Optimal Algorithms for Private Online Learning in a Stochastic Environment

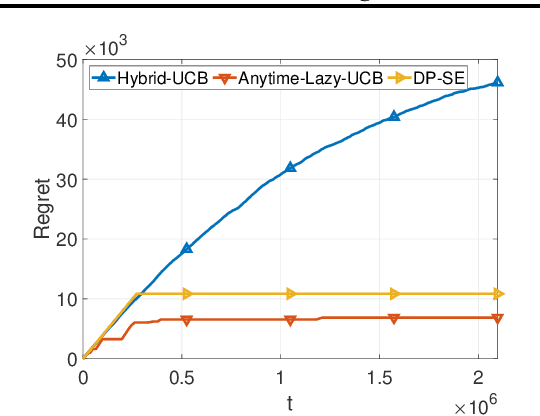
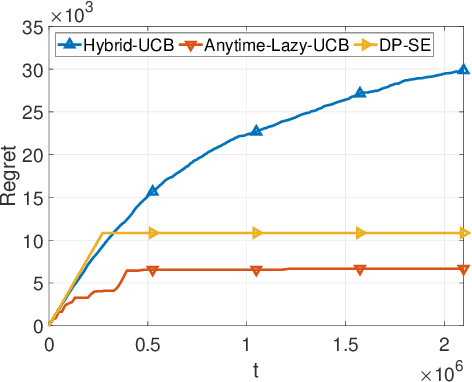
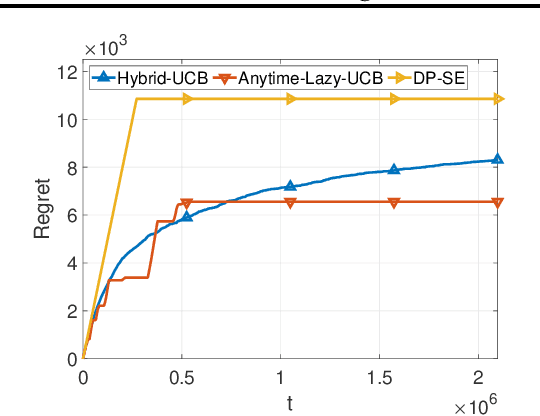
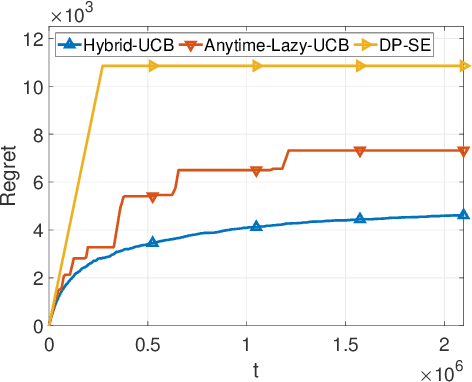
We consider two variants of private stochastic online learning. The first variant is differentially private stochastic bandits. Previously, Sajed and Sheffet (2019) devised the DP Successive Elimination (DP-SE) algorithm that achieves the optimal $ O \biggl(\sum\limits_{1\le j \le K: \Delta_j >0} \frac{ \log T}{ \Delta_j} + \frac{ K\log T}{\epsilon} \biggr)$ problem-dependent regret bound, where $K$ is the number of arms, $\Delta_j$ is the mean reward gap of arm $j$, $T$ is the time horizon, and $\epsilon$ is the required privacy parameter. However, like other elimination style algorithms, it is not an anytime algorithm. Until now, it was not known whether UCB-based algorithms could achieve this optimal regret bound. We present an anytime, UCB-based algorithm that achieves optimality. Our experiments show that the UCB-based algorithm is competitive with DP-SE. The second variant is the full information version of private stochastic online learning. Specifically, for the problems of decision-theoretic online learning with stochastic rewards, we present the first algorithm that achieves an $ O \left( \frac{ \log K}{ \Delta_{\min}} + \frac{ \log K}{\epsilon} \right)$ regret bound, where $\Delta_{\min}$ is the minimum mean reward gap. The key idea behind our good theoretical guarantees in both settings is the forgetfulness, i.e., decisions are made based on a certain amount of newly obtained observations instead of all the observations obtained from the very beginning.

A Farewell to Arms: Sequential Reward Maximization on a Budget with a Giving Up Option

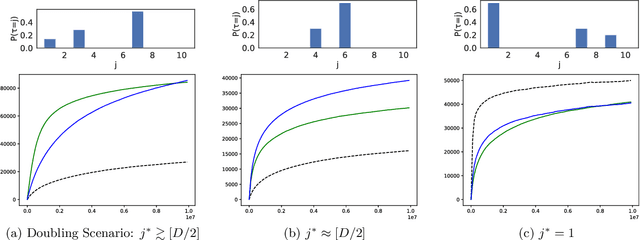
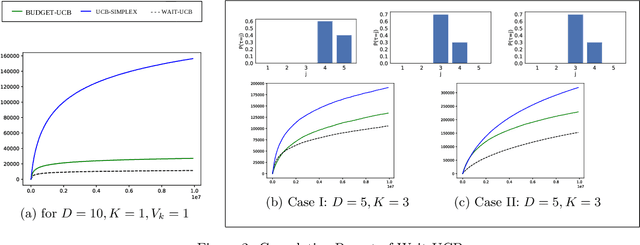
We consider a sequential decision-making problem where an agent can take one action at a time and each action has a stochastic temporal extent, i.e., a new action cannot be taken until the previous one is finished. Upon completion, the chosen action yields a stochastic reward. The agent seeks to maximize its cumulative reward over a finite time budget, with the option of "giving up" on a current action --- hence forfeiting any reward -- in order to choose another action. We cast this problem as a variant of the stochastic multi-armed bandits problem with stochastic consumption of resource. For this problem, we first establish that the optimal arm is the one that maximizes the ratio of the expected reward of the arm to the expected waiting time before the agent sees the reward due to pulling that arm. Using a novel upper confidence bound on this ratio, we then introduce an upper confidence based-algorithm, WAIT-UCB, for which we establish logarithmic, problem-dependent regret bound which has an improved dependence on problem parameters compared to previous works. Simulations on various problem configurations comparing WAIT-UCB against the state-of-the-art algorithms are also presented.