No-regret incentive-compatible online learning under exact truthfulness with non-myopic experts

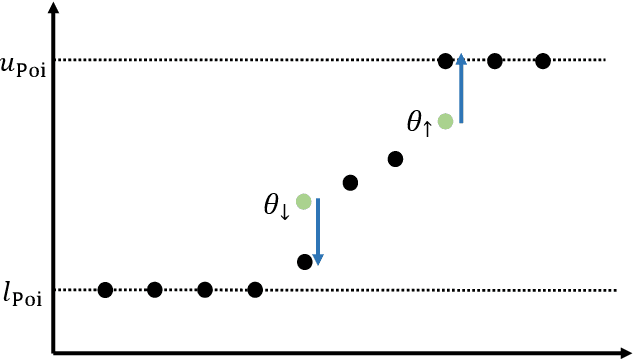
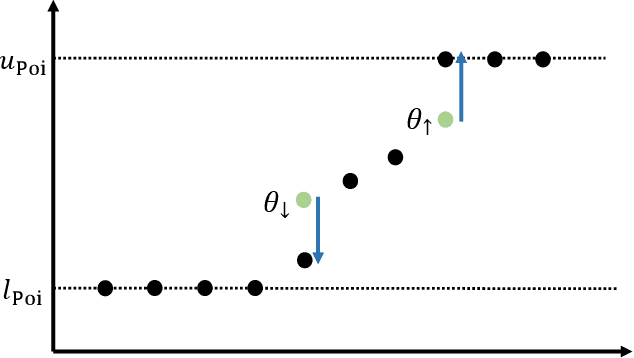
We study an online forecasting setting in which, over $T$ rounds, $N$ strategic experts each report a forecast to a mechanism, the mechanism selects one forecast, and then the outcome is revealed. In any given round, each expert has a belief about the outcome, but the expert wishes to select its report so as to maximize the total number of times it is selected. The goal of the mechanism is to obtain low belief regret: the difference between its cumulative loss (based on its selected forecasts) and the cumulative loss of the best expert in hindsight (as measured by the experts' beliefs). We consider exactly truthful mechanisms for non-myopic experts, meaning that truthfully reporting its belief strictly maximizes the expert's subjective probability of being selected in any future round. Even in the full-information setting, it is an open problem to obtain the first no-regret exactly truthful mechanism in this setting. We develop the first no-regret mechanism for this setting via an online extension of the Independent-Event Lotteries Forecasting Competition Mechanism (I-ELF). By viewing this online I-ELF as a novel instance of Follow the Perturbed Leader (FPL) with noise based on random walks with loss-dependent perturbations, we obtain $\tilde{O}(\sqrt{T N})$ regret. Our results are fueled by new tail bounds for Poisson binomial random variables that we develop. We extend our results to the bandit setting, where we give an exactly truthful mechanism obtaining $\tilde{O}(T^{2/3} N^{1/3})$ regret; this is the first no-regret result even among approximately truthful mechanisms.

Data-dependent Bounds with $T$-Optimal Best-of-Both-Worlds Guarantees in Multi-Armed Bandits using Stability-Penalty Matching

Existing data-dependent and best-of-both-worlds regret bounds for multi-armed bandits problems have limited adaptivity as they are either data-dependent but not best-of-both-worlds (BOBW), BOBW but not data-dependent or have sub-optimal $O(\sqrt{T\ln{T}})$ worst-case guarantee in the adversarial regime. To overcome these limitations, we propose real-time stability-penalty matching (SPM), a new method for obtaining regret bounds that are simultaneously data-dependent, best-of-both-worlds and $T$-optimal for multi-armed bandits problems. In particular, we show that real-time SPM obtains bounds with worst-case guarantees of order $O(\sqrt{T})$ in the adversarial regime and $O(\ln{T})$ in the stochastic regime while simultaneously being adaptive to data-dependent quantities such as sparsity, variations, and small losses. Our results are obtained by extending the SPM technique for tuning the learning rates in the follow-the-regularized-leader (FTRL) framework, which further indicates that the combination of SPM and FTRL is a promising approach for proving new adaptive bounds in online learning problems.

Fixed Confidence Best Arm Identification in the Bayesian Setting

We consider the fixed-confidence best arm identification (FC-BAI) problem in the Bayesian Setting. This problem aims to find the arm of the largest mean with a fixed confidence level when the bandit model has been sampled from the known prior. Most studies on the FC-BAI problem have been conducted in the frequentist setting, where the bandit model is predetermined before the game starts. We show that the traditional FC-BAI algorithms studied in the frequentist setting, such as track-and-stop and top-two algorithms, result in arbitrary suboptimal performances in the Bayesian setting. We also prove a lower bound of the expected number of samples in the Bayesian setting and introduce a variant of successive elimination that has a matching performance with the lower bound up to a logarithmic factor. Simulations verify the theoretical results.

Replicability is Asymptotically Free in Multi-armed Bandits

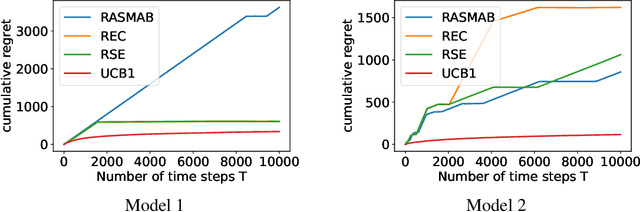
This work is motivated by the growing demand for reproducible machine learning. We study the stochastic multi-armed bandit problem. In particular, we consider a replicable algorithm that ensures, with high probability, that the algorithm's sequence of actions is not affected by the randomness inherent in the dataset. We observe that existing algorithms require $O(1/\rho^2)$ times more regret than nonreplicable algorithms, where $\rho$ is the level of nonreplication. However, we demonstrate that this additional cost is unnecessary when the time horizon $T$ is sufficiently large for a given $\rho$, provided that the magnitude of the confidence bounds is chosen carefully. We introduce an explore-then-commit algorithm that draws arms uniformly before committing to a single arm. Additionally, we examine a successive elimination algorithm that eliminates suboptimal arms at the end of each phase. To ensure the replicability of these algorithms, we incorporate randomness into their decision-making processes. We extend the use of successive elimination to the linear bandit problem as well. For the analysis of these algorithms, we propose a principled approach to limiting the probability of nonreplication. This approach elucidates the steps that existing research has implicitly followed. Furthermore, we derive the first lower bound for the two-armed replicable bandit problem, which implies the optimality of the proposed algorithms up to a $\log\log T$ factor for the two-armed case.

Learning Fair Division from Bandit Feedback

This work addresses learning online fair division under uncertainty, where a central planner sequentially allocates items without precise knowledge of agents' values or utilities. Departing from conventional online algorithm, the planner here relies on noisy, estimated values obtained after allocating items. We introduce wrapper algorithms utilizing \textit{dual averaging}, enabling gradual learning of both the type distribution of arriving items and agents' values through bandit feedback. This approach enables the algorithms to asymptotically achieve optimal Nash social welfare in linear Fisher markets with agents having additive utilities. We establish regret bounds in Nash social welfare and empirically validate the superior performance of our proposed algorithms across synthetic and empirical datasets.

High-dimensional Contextual Bandit Problem without Sparsity

In this research, we investigate the high-dimensional linear contextual bandit problem where the number of features $p$ is greater than the budget $T$, or it may even be infinite. Differing from the majority of previous works in this field, we do not impose sparsity on the regression coefficients. Instead, we rely on recent findings on overparameterized models, which enables us to analyze the performance the minimum-norm interpolating estimator when data distributions have small effective ranks. We propose an explore-then-commit (EtC) algorithm to address this problem and examine its performance. Through our analysis, we derive the optimal rate of the ETC algorithm in terms of $T$ and show that this rate can be achieved by balancing exploration and exploitation. Moreover, we introduce an adaptive explore-then-commit (AEtC) algorithm that adaptively finds the optimal balance. We assess the performance of the proposed algorithms through a series of simulations.

Globally Optimal Algorithms for Fixed-Budget Best Arm Identification

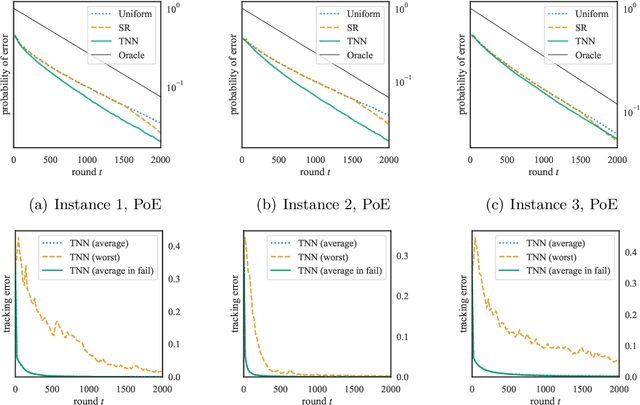
We consider the fixed-budget best arm identification problem where the goal is to find the arm of the largest mean with a fixed number of samples. It is known that the probability of misidentifying the best arm is exponentially small to the number of rounds. However, limited characterizations have been discussed on the rate (exponent) of this value. In this paper, we characterize the optimal rate as a result of global optimization over all possible parameters. We introduce two rates, $R^{\mathrm{go}}$ and $R^{\mathrm{go}}_{\infty}$, corresponding to lower bounds on the misidentification probability, each of which is associated with a proposed algorithm. The rate $R^{\mathrm{go}}$ is associated with $R^{\mathrm{go}}$-tracking, which can be efficiently implemented by a neural network and is shown to outperform existing algorithms. However, this rate requires a nontrivial condition to be achievable. To deal with this issue, we introduce the second rate $R^{\mathrm{go}}_\infty$. We show that this rate is indeed achievable by introducing a conceptual algorithm called delayed optimal tracking (DOT).

Anytime Capacity Expansion in Medical Residency Match by Monte Carlo Tree Search

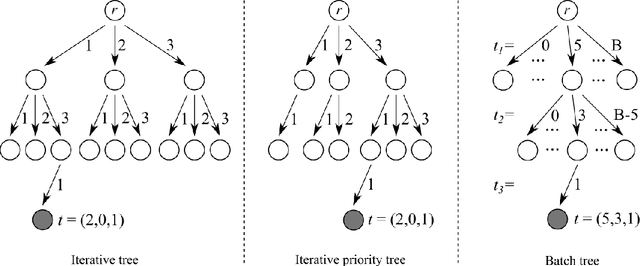
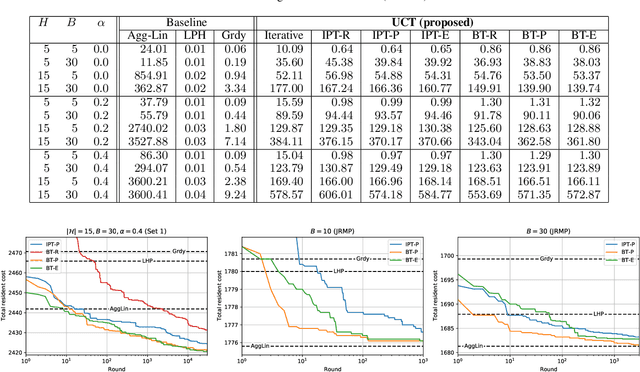
This paper considers the capacity expansion problem in two-sided matchings, where the policymaker is allowed to allocate some extra seats as well as the standard seats. In medical residency match, each hospital accepts a limited number of doctors. Such capacity constraints are typically given in advance. However, such exogenous constraints can compromise the welfare of the doctors; some popular hospitals inevitably dismiss some of their favorite doctors. Meanwhile, it is often the case that the hospitals are also benefited to accept a few extra doctors. To tackle the problem, we propose an anytime method that the upper confidence tree searches the space of capacity expansions, each of which has a resident-optimal stable assignment that the deferred acceptance method finds. Constructing a good search tree representation significantly boosts the performance of the proposed method. Our simulation shows that the proposed method identifies an almost optimal capacity expansion with a significantly smaller computational budget than exact methods based on mixed-integer programming.

Bayes Optimal Algorithm is Suboptimal in Frequentist Best Arm Identification

We consider the fixed-budget best arm identification problem with Normal rewards. In this problem, the forecaster is given $K$ arms (treatments) and $T$ time steps. The forecaster attempts to find the best arm in terms of the largest mean via an adaptive experiment conducted with an algorithm. The performance of the algorithm is measured by the simple regret, or the quality of the estimated best arm. It is known that the frequentist simple regret can be exponentially small to $T$ for any fixed parameters, whereas the Bayesian simple regret is $\Theta(T^{-1})$ over a continuous prior distribution. This paper shows that Bayes optimal algorithm, which minimizes the Bayesian simple regret, does not have an exponential simple regret for some parameters. This finding contrasts with the many results indicating the asymptotic equivalence of Bayesian and frequentist algorithms in fixed sampling regimes. While the Bayes optimal algorithm is described in terms of a recursive equation that is virtually impossible to compute exactly, we pave the way to an analysis by introducing a key quantity that we call the expected Bellman improvement.

Optimal Simple Regret in Bayesian Best Arm Identification

We consider Bayesian best arm identification in the multi-armed bandit problem. Assuming certain continuity conditions of the prior, we characterize the rate of the Bayesian simple regret. Differing from Bayesian regret minimization (Lai, 1987), the leading factor in Bayesian simple regret derives from the region where the gap between optimal and sub-optimal arms is smaller than $\sqrt{\frac{\log T}{T}}$. We propose a simple and easy-to-compute algorithm with its leading factor matches with the lower bound up to a constant factor; simulation results support our theoretical findings.