Approximate State Abstraction for Markov Games

This paper introduces state abstraction for two-player zero-sum Markov games (TZMGs), where the payoffs for the two players are determined by the state representing the environment and their respective actions, with state transitions following Markov decision processes. For example, in games like soccer, the value of actions changes according to the state of play, and thus such games should be described as Markov games. In TZMGs, as the number of states increases, computing equilibria becomes more difficult. Therefore, we consider state abstraction, which reduces the number of states by treating multiple different states as a single state. There is a substantial body of research on finding optimal policies for Markov decision processes using state abstraction. However, in the multi-player setting, the game with state abstraction may yield different equilibrium solutions from those of the ground game. To evaluate the equilibrium solutions of the game with state abstraction, we derived bounds on the duality gap, which represents the distance from the equilibrium solutions of the ground game. Finally, we demonstrate our state abstraction with Markov Soccer, compute equilibrium policies, and examine the results.

Learning Fair Division from Bandit Feedback

This work addresses learning online fair division under uncertainty, where a central planner sequentially allocates items without precise knowledge of agents' values or utilities. Departing from conventional online algorithm, the planner here relies on noisy, estimated values obtained after allocating items. We introduce wrapper algorithms utilizing \textit{dual averaging}, enabling gradual learning of both the type distribution of arriving items and agents' values through bandit feedback. This approach enables the algorithms to asymptotically achieve optimal Nash social welfare in linear Fisher markets with agents having additive utilities. We establish regret bounds in Nash social welfare and empirically validate the superior performance of our proposed algorithms across synthetic and empirical datasets.

A Slingshot Approach to Learning in Monotone Games

In this paper, we address the problem of computing equilibria in monotone games. The traditional Follow the Regularized Leader algorithms fail to converge to an equilibrium even in two-player zero-sum games. Although optimistic versions of these algorithms have been proposed with last-iterate convergence guarantees, they require noiseless gradient feedback. To overcome this limitation, we present a novel framework that achieves last-iterate convergence even in the presence of noise. Our key idea involves perturbing or regularizing the payoffs or utilities of the games. This perturbation serves to pull the current strategy to an anchored strategy, which we refer to as a {\it slingshot} strategy. First, we establish the convergence rates of our framework to a stationary point near an equilibrium, regardless of the presence or absence of noise. Next, we introduce an approach to periodically update the slingshot strategy with the current strategy. We interpret this approach as a proximal point method and demonstrate its last-iterate convergence. Our framework is comprehensive, incorporating existing payoff-regularized algorithms and enabling the development of new algorithms with last-iterate convergence properties. Finally, we show that our algorithms, based on this framework, empirically exhibit faster convergence.

Last-Iterate Convergence with Full- and Noisy-Information Feedback in Two-Player Zero-Sum Games

The theory of learning in games is prominent in the AI community, motivated by several rising applications such as multi-agent reinforcement learning and Generative Adversarial Networks. We propose Mutation-driven Multiplicative Weights Update (M2WU) for learning an equilibrium in two-player zero-sum normal-form games and prove that it exhibits the last-iterate convergence property in both full- and noisy-information feedback settings. In the full-information feedback setting, the players observe their exact gradient vectors of the utility functions. On the other hand, in the noisy-information feedback setting, they can only observe the noisy gradient vectors. Existing algorithms, including the well-known Multiplicative Weights Update (MWU) and Optimistic MWU (OMWU) algorithms, fail to converge to a Nash equilibrium with noisy-information feedback. In contrast, M2WU exhibits the last-iterate convergence to a stationary point near a Nash equilibrium in both of the feedback settings. We then prove that it converges to an exact Nash equilibrium by adapting the mutation term iteratively. We empirically confirm that M2WU outperforms MWU and OMWU in exploitability and convergence rates.

Mutation-Driven Follow the Regularized Leader for Last-Iterate Convergence in Zero-Sum Games

In this study, we consider a variant of the Follow the Regularized Leader (FTRL) dynamics in two-player zero-sum games. FTRL is guaranteed to converge to a Nash equilibrium when time-averaging the strategies, while a lot of variants suffer from the issue of limit cycling behavior, i.e., lack the last-iterate convergence guarantee. To this end, we propose mutant FTRL (M-FTRL), an algorithm that introduces mutation for the perturbation of action probabilities. We then investigate the continuous-time dynamics of M-FTRL and provide the strong convergence guarantees toward stationary points that approximate Nash equilibria under full-information feedback. Furthermore, our simulation demonstrates that M-FTRL can enjoy faster convergence rates than FTRL and optimistic FTRL under full-information feedback and surprisingly exhibits clear convergence under bandit feedback.

Anytime Capacity Expansion in Medical Residency Match by Monte Carlo Tree Search

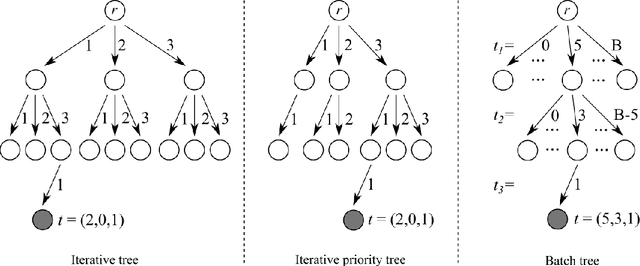
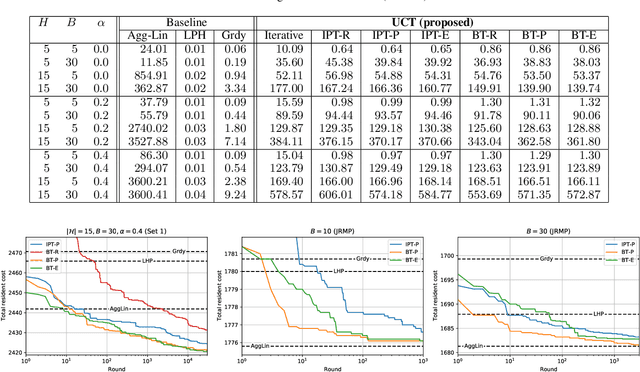
This paper considers the capacity expansion problem in two-sided matchings, where the policymaker is allowed to allocate some extra seats as well as the standard seats. In medical residency match, each hospital accepts a limited number of doctors. Such capacity constraints are typically given in advance. However, such exogenous constraints can compromise the welfare of the doctors; some popular hospitals inevitably dismiss some of their favorite doctors. Meanwhile, it is often the case that the hospitals are also benefited to accept a few extra doctors. To tackle the problem, we propose an anytime method that the upper confidence tree searches the space of capacity expansions, each of which has a resident-optimal stable assignment that the deferred acceptance method finds. Constructing a good search tree representation significantly boosts the performance of the proposed method. Our simulation shows that the proposed method identifies an almost optimal capacity expansion with a significantly smaller computational budget than exact methods based on mixed-integer programming.