Anytime Capacity Expansion in Medical Residency Match by Monte Carlo Tree Search
Paper and Code
Feb 14, 2022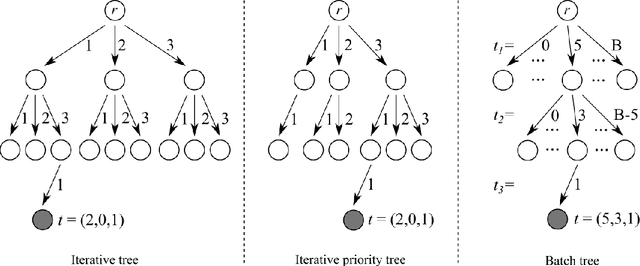

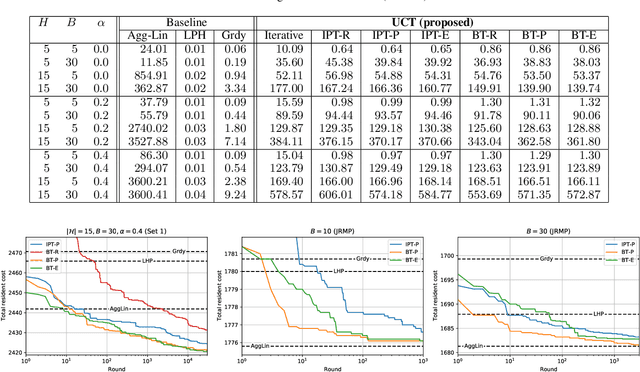

This paper considers the capacity expansion problem in two-sided matchings, where the policymaker is allowed to allocate some extra seats as well as the standard seats. In medical residency match, each hospital accepts a limited number of doctors. Such capacity constraints are typically given in advance. However, such exogenous constraints can compromise the welfare of the doctors; some popular hospitals inevitably dismiss some of their favorite doctors. Meanwhile, it is often the case that the hospitals are also benefited to accept a few extra doctors. To tackle the problem, we propose an anytime method that the upper confidence tree searches the space of capacity expansions, each of which has a resident-optimal stable assignment that the deferred acceptance method finds. Constructing a good search tree representation significantly boosts the performance of the proposed method. Our simulation shows that the proposed method identifies an almost optimal capacity expansion with a significantly smaller computational budget than exact methods based on mixed-integer programming.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge