Policy Testing in Markov Decision Processes

We study the policy testing problem in discounted Markov decision processes (MDPs) under the fixed-confidence setting. The goal is to determine whether the value of a given policy exceeds a specified threshold while minimizing the number of observations. We begin by deriving an instance-specific lower bound that any algorithm must satisfy. This lower bound is characterized as the solution to an optimization problem with non-convex constraints. We propose a policy testing algorithm inspired by this optimization problem--a common approach in pure exploration problems such as best-arm identification, where asymptotically optimal algorithms often stem from such optimization-based characterizations. As for other pure exploration tasks in MDPs, however, the non-convex constraints in the lower-bound problem present significant challenges, raising doubts about whether statistically optimal and computationally tractable algorithms can be designed. To address this, we reformulate the lower-bound problem by interchanging the roles of the objective and the constraints, yielding an alternative problem with a non-convex objective but convex constraints. Strikingly, this reformulated problem admits an interpretation as a policy optimization task in a newly constructed reversed MDP. Leveraging recent advances in policy gradient methods, we efficiently solve this problem and use it to design a policy testing algorithm that is statistically optimal--matching the instance-specific lower bound on sample complexity--while remaining computationally tractable. We validate our approach with numerical experiments.

Evaluation of Best-of-N Sampling Strategies for Language Model Alignment

Best-of-N (BoN) sampling with a reward model has been shown to be an effective strategy for aligning Large Language Models (LLMs) with human preferences at the time of decoding. BoN sampling is susceptible to a problem known as reward hacking. Since the reward model is an imperfect proxy for the true objective, an excessive focus on optimizing its value can lead to a compromise of its performance on the true objective. Previous work proposes Regularized BoN sampling (RBoN), a BoN sampling with regularization to the objective, and shows that it outperforms BoN sampling so that it mitigates reward hacking and empirically (Jinnai et al., 2024). However, Jinnai et al. (2024) introduce RBoN based on a heuristic and they lack the analysis of why such regularization strategy improves the performance of BoN sampling. The aim of this study is to analyze the effect of BoN sampling on regularization strategies. Using the regularization strategies corresponds to robust optimization, which maximizes the worst case over a set of possible perturbations in the proxy reward. Although the theoretical guarantees are not directly applicable to RBoN, RBoN corresponds to a practical implementation. This paper proposes an extension of the RBoN framework, called Stochastic RBoN sampling (SRBoN), which is a theoretically guaranteed approach to worst-case RBoN in proxy reward. We then perform an empirical evaluation using the AlpacaFarm and Anthropic's hh-rlhf datasets to evaluate which factors of the regularization strategies contribute to the improvement of the true proxy reward. In addition, we also propose another simple RBoN method, the Sentence Length Regularized BoN, which has a better performance in the experiment as compared to the previous methods.

Theoretical Guarantees for Minimum Bayes Risk Decoding

Minimum Bayes Risk (MBR) decoding optimizes output selection by maximizing the expected utility value of an underlying human distribution. While prior work has shown the effectiveness of MBR decoding through empirical evaluation, few studies have analytically investigated why the method is effective. As a result of our analysis, we show that, given the size $n$ of the reference hypothesis set used in computation, MBR decoding approaches the optimal solution with high probability at a rate of $O\left(n^{-\frac{1}{2}}\right)$, under certain assumptions, even though the language space $Y$ is significantly larger $Y\gg n$. This result helps to theoretically explain the strong performance observed in several prior empirical studies on MBR decoding. In addition, we provide the performance gap for maximum-a-posteriori (MAP) decoding and compare it to MBR decoding. The result of this paper indicates that MBR decoding tends to converge to the optimal solution faster than MAP decoding in several cases.

The Power of Perturbation under Sampling in Solving Extensive-Form Games

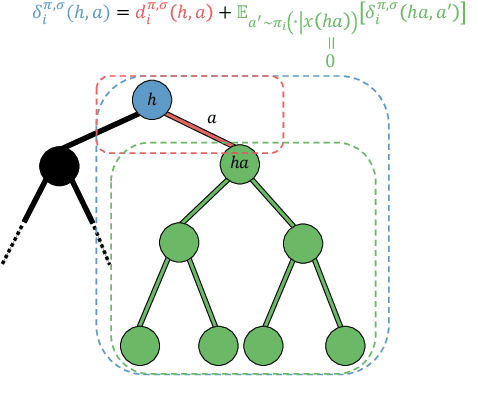
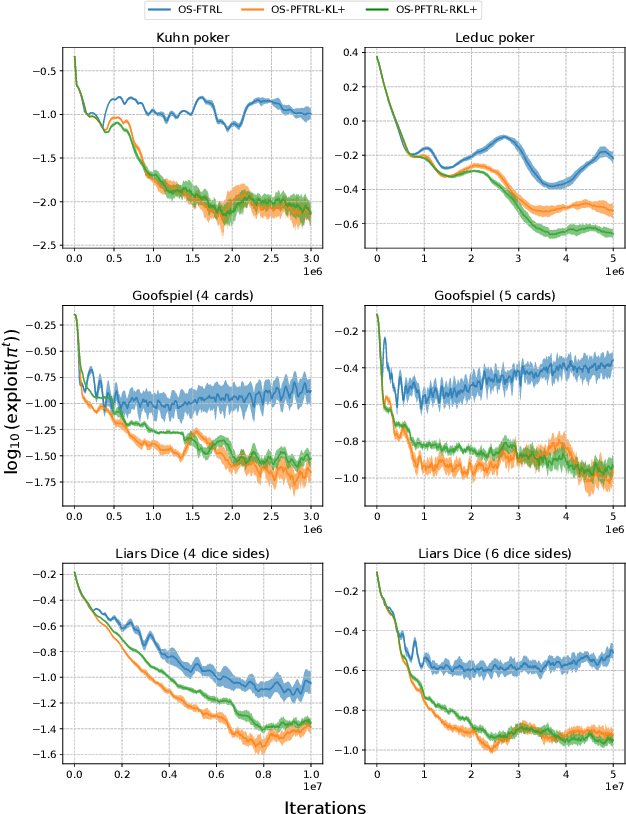
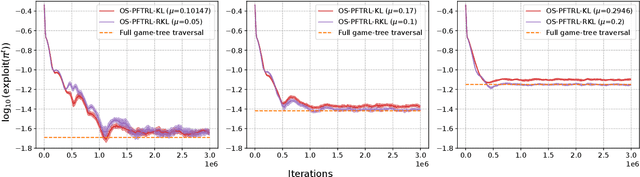
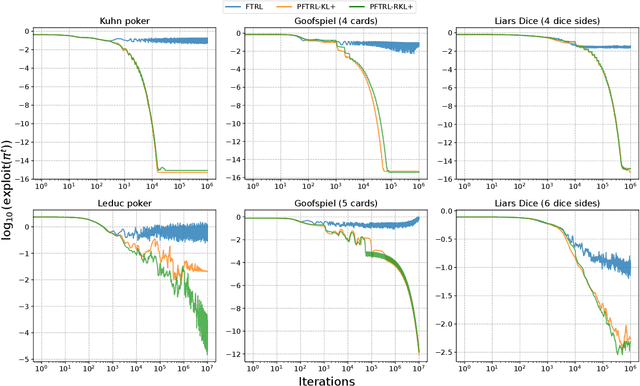
This paper investigates how perturbation does and does not improve the Follow-the-Regularized-Leader (FTRL) algorithm in imperfect-information extensive-form games. Perturbing the expected payoffs guarantees that the FTRL dynamics reach an approximate equilibrium, and proper adjustments of the magnitude of the perturbation lead to a Nash equilibrium (\textit{last-iterate convergence}). This approach is robust even when payoffs are estimated using sampling -- as is the case for large games -- while the optimistic approach often becomes unstable. Building upon those insights, we first develop a general framework for perturbed FTRL algorithms under \textit{sampling}. We then empirically show that in the last-iterate sense, the perturbed FTRL consistently outperforms the non-perturbed FTRL. We further identify a divergence function that reduces the variance of the estimates for perturbed payoffs, with which it significantly outperforms the prior algorithms on Leduc poker (whose structure is more asymmetric in a sense than that of the other benchmark games) and consistently performs smooth convergence behavior on all the benchmark games.

Last Iterate Convergence in Monotone Mean Field Games

Mean Field Game (MFG) is a framework utilized to model and approximate the behavior of a large number of agents, and the computation of equilibria in MFG has been a subject of interest. Despite the proposal of methods to approximate the equilibria, algorithms where the sequence of updated policy converges to equilibrium, specifically those exhibiting last-iterate convergence, have been limited. We propose the use of a simple, proximal-point-type algorithm to compute equilibria for MFGs. Subsequently, we provide the first last-iterate convergence guarantee under the Lasry--Lions-type monotonicity condition. We further employ the Mirror Descent algorithm for the regularized MFG to efficiently approximate the update rules of the proximal point method for MFGs. We demonstrate that the algorithm can approximate with an accuracy of $\varepsilon$ after $\mathcal{O}({\log(1/\varepsilon)})$ iterations. This research offers a tractable approach for large-scale and large-population games.

Matroid Semi-Bandits in Sublinear Time

We study the matroid semi-bandits problem, where at each round the learner plays a subset of $K$ arms from a feasible set, and the goal is to maximize the expected cumulative linear rewards. Existing algorithms have per-round time complexity at least $\Omega(K)$, which becomes expensive when $K$ is large. To address this computational issue, we propose FasterCUCB whose sampling rule takes time sublinear in $K$ for common classes of matroids: $O(D\text{ polylog}(K)\text{ polylog}(T))$ for uniform matroids, partition matroids, and graphical matroids, and $O(D\sqrt{K}\text{ polylog}(T))$ for transversal matroids. Here, $D$ is the maximum number of elements in any feasible subset of arms, and $T$ is the horizon. Our technique is based on dynamic maintenance of an approximate maximum-weight basis over inner-product weights. Although the introduction of an approximate maximum-weight basis presents a challenge in regret analysis, we can still guarantee an upper bound on regret as tight as CUCB in the sense that it matches the gap-dependent lower bound by Kveton et al. (2014a) asymptotically.

Filtered Direct Preference Optimization

Reinforcement learning from human feedback (RLHF) plays a crucial role in aligning language models with human preferences. While the significance of dataset quality is generally recognized, explicit investigations into its impact within the RLHF framework, to our knowledge, have been limited. This paper addresses the issue of text quality within the preference dataset by focusing on Direct Preference Optimization (DPO), an increasingly adopted reward-model-free RLHF method. We confirm that text quality significantly influences the performance of models optimized with DPO more than those optimized with reward-model-based RLHF. Building on this new insight, we propose an extension of DPO, termed filtered direct preference optimization (fDPO). fDPO uses a trained reward model to monitor the quality of texts within the preference dataset during DPO training. Samples of lower quality are discarded based on comparisons with texts generated by the model being optimized, resulting in a more accurate dataset. Experimental results demonstrate that fDPO enhances the final model performance. Our code is available at https://github.com/CyberAgentAILab/filtered-dpo.

Regularized Best-of-N Sampling to Mitigate Reward Hacking for Language Model Alignment

Best-of-N (BoN) sampling with a reward model has been shown to be an effective strategy for aligning Large Language Models (LLMs) to human preferences at the time of decoding. BoN sampling is susceptible to a problem known as reward hacking. Because the reward model is an imperfect proxy for the true objective, over-optimizing its value can compromise its performance on the true objective. A common solution to prevent reward hacking in preference learning techniques is to optimize a reward using proximity regularization (e.g., KL regularization), which ensures that the language model remains close to the reference model. In this research, we propose Regularized Best-of-N (RBoN), a variant of BoN that aims to mitigate reward hacking by incorporating a proximity term in response selection, similar to preference learning techniques. We evaluate two variants of RBoN on the AlpacaFarm dataset and find that they outperform BoN, especially when the proxy reward model has a low correlation with the true objective.

Return-Aligned Decision Transformer

Traditional approaches in offline reinforcement learning aim to learn the optimal policy that maximizes the cumulative reward, also known as return. However, as applications broaden, it becomes increasingly crucial to train agents that not only maximize the returns, but align the actual return with a specified target return, giving control over the agent's performance. Decision Transformer (DT) optimizes a policy that generates actions conditioned on the target return through supervised learning and is equipped with a mechanism to control the agent using the target return. Despite being designed to align the actual return with the target return, we have empirically identified a discrepancy between the actual return and the target return in DT. In this paper, we propose Return-Aligned Decision Transformer (RADT), designed to effectively align the actual return with the target return. Our model decouples returns from the conventional input sequence, which typically consists of returns, states, and actions, to enhance the relationships between returns and states, as well as returns and actions. Extensive experiments show that RADT reduces the discrepancies between the actual return and the target return of DT-based methods.

Hyperparameter-Free Approach for Faster Minimum Bayes Risk Decoding

Minimum Bayes-Risk (MBR) decoding is shown to be a powerful alternative to beam search decoding for a wide range of text generation tasks. However, MBR requires a huge amount of time for inference to compute the MBR objective, which makes the method infeasible in many situations where response time is critical. Confidence-based pruning (CBP) (Cheng and Vlachos, 2023) has recently been proposed to reduce the inference time in machine translation tasks. Although it is shown to significantly reduce the amount of computation, it requires hyperparameter tuning using a development set to be effective. To this end, we propose Approximate Minimum Bayes-Risk (AMBR) decoding, a hyperparameter-free method to run MBR decoding approximately. AMBR is derived from the observation that the problem of computing the sample-based MBR objective is the medoid identification problem. AMBR uses the Correlated Sequential Halving (CSH) algorithm (Baharav and Tse, 2019), the best approximation algorithm to date for the medoid identification problem, to compute the sample-based MBR objective. We evaluate AMBR on machine translation, text summarization, and image captioning tasks. The results show that AMBR achieves on par with CBP, with CBP selecting hyperparameters through an Oracle for each given computation budget.