Sinkhorn Algorithm for Sequentially Composed Optimal Transports

Sinkhorn algorithm is the de-facto standard approximation algorithm for optimal transport, which has been applied to a variety of applications, including image processing and natural language processing. In theory, the proof of its convergence follows from the convergence of the Sinkhorn--Knopp algorithm for the matrix scaling problem, and Altschuler et al. show that its worst-case time complexity is in near-linear time. Very recently, sequentially composed optimal transports were proposed by Watanabe and Isobe as a hierarchical extension of optimal transports. In this paper, we present an efficient approximation algorithm, namely Sinkhorn algorithm for sequentially composed optimal transports, for its entropic regularization. Furthermore, we present a theoretical analysis of the Sinkhorn algorithm, namely (i) its exponential convergence to the optimal solution with respect to the Hilbert pseudometric, and (ii) a worst-case complexity analysis for the case of one sequential composition.

Last Iterate Convergence in Monotone Mean Field Games

Mean Field Game (MFG) is a framework utilized to model and approximate the behavior of a large number of agents, and the computation of equilibria in MFG has been a subject of interest. Despite the proposal of methods to approximate the equilibria, algorithms where the sequence of updated policy converges to equilibrium, specifically those exhibiting last-iterate convergence, have been limited. We propose the use of a simple, proximal-point-type algorithm to compute equilibria for MFGs. Subsequently, we provide the first last-iterate convergence guarantee under the Lasry--Lions-type monotonicity condition. We further employ the Mirror Descent algorithm for the regularized MFG to efficiently approximate the update rules of the proximal point method for MFGs. We demonstrate that the algorithm can approximate with an accuracy of $\varepsilon$ after $\mathcal{O}({\log(1/\varepsilon)})$ iterations. This research offers a tractable approach for large-scale and large-population games.

String Diagram of Optimal Transports

We propose a hierarchical framework of optimal transports (OTs), namely string diagrams of OTs. Our target problem is a safety problem on string diagrams of OTs, which requires proving or disproving that the minimum transportation cost in a given string diagram of OTs is above a given threshold. We reduce the safety problem on a string diagram of OTs to that on a monolithic OT by composing cost matrices. Our novel reduction exploits an algebraic structure of cost matrices equipped with two compositions: a sequential composition and a parallel composition. We provide a novel algorithm for the safety problem on string diagrams of OTs by our reduction, and we demonstrate its efficiency and performance advantage through experiments.

Flow matching achieves minimax optimal convergence

Flow matching (FM) has gained significant attention as a simulation-free generative model. Unlike diffusion models, which are based on stochastic differential equations, FM employs a simpler approach by solving an ordinary differential equation with an initial condition from a normal distribution, thus streamlining the sample generation process. This paper discusses the convergence properties of FM in terms of the $p$-Wasserstein distance, a measure of distributional discrepancy. We establish that FM can achieve the minmax optimal convergence rate for $1 \leq p \leq 2$, presenting the first theoretical evidence that FM can reach convergence rates comparable to those of diffusion models. Our analysis extends existing frameworks by examining a broader class of mean and variance functions for the vector fields and identifies specific conditions necessary to attain these optimal rates.

Extended Flow Matching: a Method of Conditional Generation with Generalized Continuity Equation

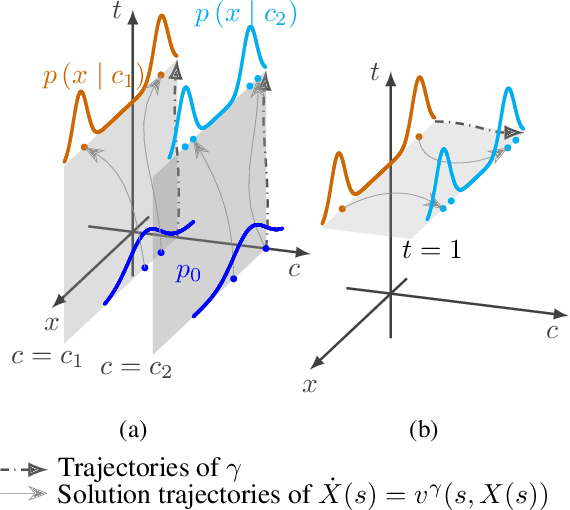
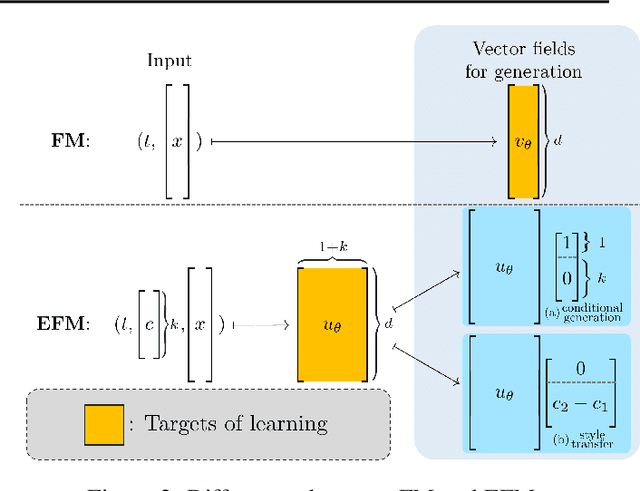
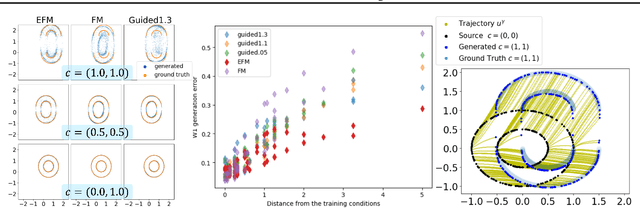
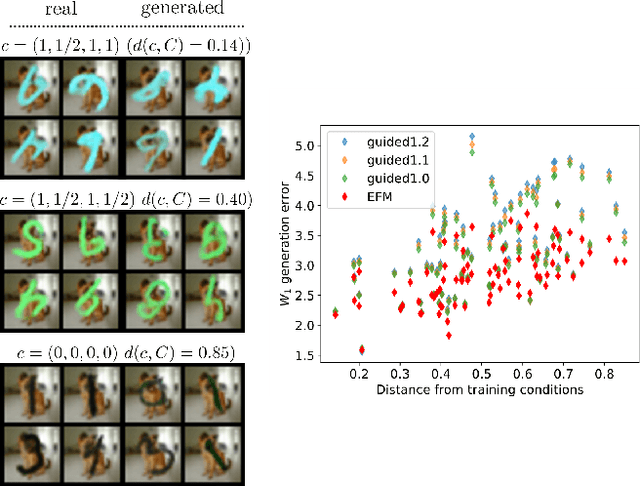
The task of conditional generation is one of the most important applications of generative models, and numerous methods have been developed to date based on the celebrated diffusion models, with the guidance-based classifier-free method taking the lead. However, the theory of the guidance-based method not only requires the user to fine-tune the "guidance strength," but its target vector field does not necessarily correspond to the conditional distribution used in training. In this paper, we develop the theory of conditional generation based on Flow Matching, a current strong contender of diffusion methods. Motivated by the interpretation of a probability path as a distribution on path space, we establish a novel theory of flow-based generation of conditional distribution by employing the mathematical framework of generalized continuity equation instead of the continuity equation in flow matching. This theory naturally derives a method that aims to match the matrix field as opposed to the vector field. Our framework ensures the continuity of the generated conditional distribution through the existence of flow between conditional distributions. We will present our theory through experiments and mathematical results.

A Convergence result of a continuous model of deep learning via Łojasiewicz--Simon inequality

This study focuses on a Wasserstein-type gradient flow, which represents an optimization process of a continuous model of a Deep Neural Network (DNN). First, we establish the existence of a minimizer for an average loss of the model under $L^2$-regularization. Subsequently, we show the existence of a curve of maximal slope of the loss. Our main result is the convergence of flow to a critical point of the loss as time goes to infinity. An essential aspect of proving this result involves the establishment of the \L{}ojasiewicz--Simon gradient inequality for the loss. We derive this inequality by assuming the analyticity of NNs and loss functions. Our proofs offer a new approach for analyzing the asymptotic behavior of Wasserstein-type gradient flows for nonconvex functionals.

Variational formulations of ODE-Net as a mean-field optimal control problem and existence results

This paper presents a mathematical analysis of ODE-Net, a continuum model of deep neural networks (DNNs). In recent years, Machine Learning researchers have introduced ideas of replacing the deep structure of DNNs with ODEs as a continuum limit. These studies regard the "learning" of ODE-Net as the minimization of a "loss" constrained by a parametric ODE. Although the existence of a minimizer for this minimization problem needs to be assumed, only a few studies have investigated its existence analytically in detail. In the present paper, the existence of a minimizer is discussed based on a formulation of ODE-Net as a measure-theoretic mean-field optimal control problem. The existence result is proved when a neural network, which describes a vector field of ODE-Net, is linear with respect to learnable parameters. The proof employs the measure-theoretic formulation combined with the direct method of Calculus of Variations. Secondly, an idealized minimization problem is proposed to remove the above linearity assumption. Such a problem is inspired by a kinetic regularization associated with the Benamou--Brenier formula and universal approximation theorems for neural networks. The proofs of these existence results use variational methods, differential equations, and mean-field optimal control theory. They will stand for a new analytic way to investigate the learning process of deep neural networks.