Extended Flow Matching: a Method of Conditional Generation with Generalized Continuity Equation

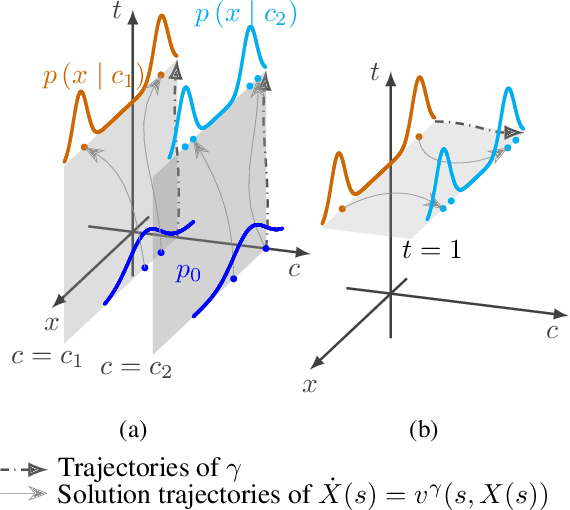
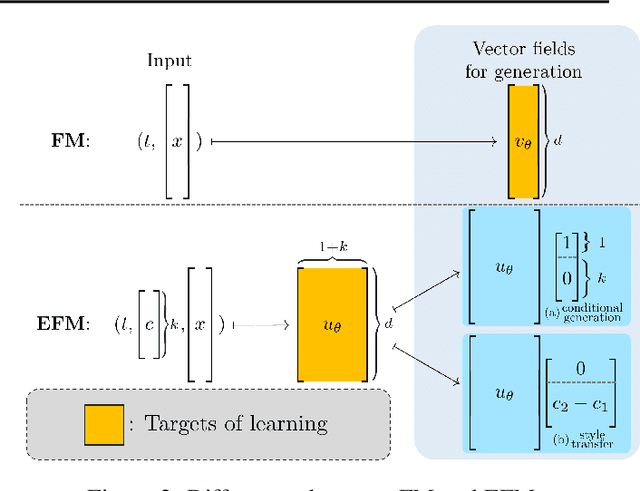
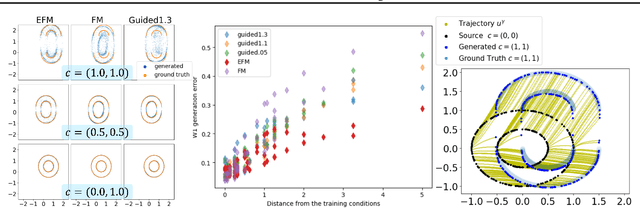
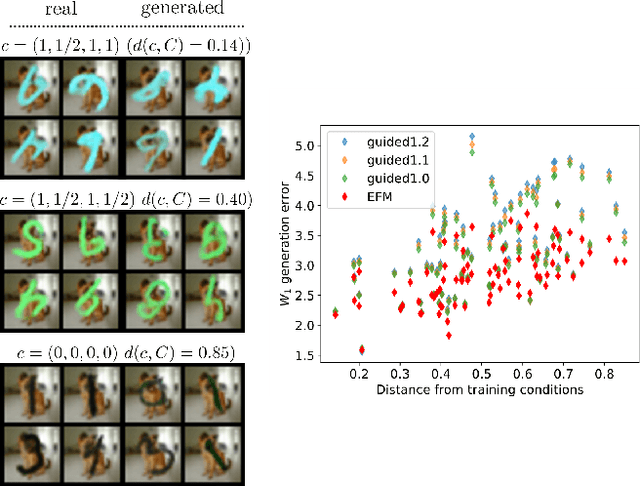
The task of conditional generation is one of the most important applications of generative models, and numerous methods have been developed to date based on the celebrated diffusion models, with the guidance-based classifier-free method taking the lead. However, the theory of the guidance-based method not only requires the user to fine-tune the "guidance strength," but its target vector field does not necessarily correspond to the conditional distribution used in training. In this paper, we develop the theory of conditional generation based on Flow Matching, a current strong contender of diffusion methods. Motivated by the interpretation of a probability path as a distribution on path space, we establish a novel theory of flow-based generation of conditional distribution by employing the mathematical framework of generalized continuity equation instead of the continuity equation in flow matching. This theory naturally derives a method that aims to match the matrix field as opposed to the vector field. Our framework ensures the continuity of the generated conditional distribution through the existence of flow between conditional distributions. We will present our theory through experiments and mathematical results.