Kenji Fukumizu
Diffusion Models with Double Guidance: Generate with aggregated datasets
May 19, 2025Abstract:Creating large-scale datasets for training high-performance generative models is often prohibitively expensive, especially when associated attributes or annotations must be provided. As a result, merging existing datasets has become a common strategy. However, the sets of attributes across datasets are often inconsistent, and their naive concatenation typically leads to block-wise missing conditions. This presents a significant challenge for conditional generative modeling when the multiple attributes are used jointly as conditions, thereby limiting the model's controllability and applicability. To address this issue, we propose a novel generative approach, Diffusion Model with Double Guidance, which enables precise conditional generation even when no training samples contain all conditions simultaneously. Our method maintains rigorous control over multiple conditions without requiring joint annotations. We demonstrate its effectiveness in molecular and image generation tasks, where it outperforms existing baselines both in alignment with target conditional distributions and in controllability under missing condition settings.
Simultaneous Learning of Optimal Transports for Training All-to-All Flow-Based Condition Transfer Model
Apr 04, 2025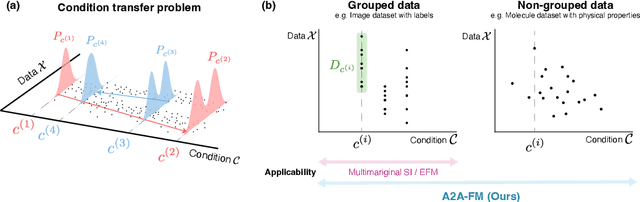

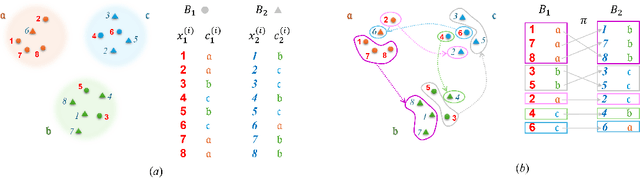

Abstract:In this paper, we propose a flow-based method for learning all-to-all transfer maps among conditional distributions, approximating pairwise optimal transport. The proposed method addresses the challenge of handling continuous conditions, which often involve a large set of conditions with sparse empirical observations per condition. We introduce a novel cost function that enables simultaneous learning of optimal transports for all pairs of conditional distributions. Our method is supported by a theoretical guarantee that, in the limit, it converges to pairwise optimal transports among infinite pairs of conditional distributions. The learned transport maps are subsequently used to couple data points in conditional flow matching. We demonstrate the effectiveness of this method on synthetic and benchmark datasets, as well as on chemical datasets where continuous physical properties are defined as conditions.
Scalable Sobolev IPM for Probability Measures on a Graph
Feb 02, 2025Abstract:We investigate the Sobolev IPM problem for probability measures supported on a graph metric space. Sobolev IPM is an important instance of integral probability metrics (IPM), and is obtained by constraining a critic function within a unit ball defined by the Sobolev norm. In particular, it has been used to compare probability measures and is crucial for several theoretical works in machine learning. However, to our knowledge, there are no efficient algorithmic approaches to compute Sobolev IPM effectively, which hinders its practical applications. In this work, we establish a relation between Sobolev norm and weighted $L^p$-norm, and leverage it to propose a \emph{novel regularization} for Sobolev IPM. By exploiting the graph structure, we demonstrate that the regularized Sobolev IPM provides a \emph{closed-form} expression for fast computation. This advancement addresses long-standing computational challenges, and paves the way to apply Sobolev IPM for practical applications, even in large-scale settings. Additionally, the regularized Sobolev IPM is negative definite. Utilizing this property, we design positive-definite kernels upon the regularized Sobolev IPM, and provide preliminary evidences of their advantages on document classification and topological data analysis for measures on a graph.
Orlicz-Sobolev Transport for Unbalanced Measures on a Graph
Feb 02, 2025



Abstract:Moving beyond $L^p$ geometric structure, Orlicz-Wasserstein (OW) leverages a specific class of convex functions for Orlicz geometric structure. While OW remarkably helps to advance certain machine learning approaches, it has a high computational complexity due to its two-level optimization formula. Recently, Le et al. (2024) exploits graph structure to propose generalized Sobolev transport (GST), i.e., a scalable variant for OW. However, GST assumes that input measures have the same mass. Unlike optimal transport (OT), it is nontrivial to incorporate a mass constraint to extend GST for measures on a graph, possibly having different total mass. In this work, we propose to take a step back by considering the entropy partial transport (EPT) for nonnegative measures on a graph. By leveraging Caffarelli & McCann (2010)'s observations, EPT can be reformulated as a standard complete OT between two corresponding balanced measures. Consequently, we develop a novel EPT with Orlicz geometric structure, namely Orlicz-EPT, for unbalanced measures on a graph. Especially, by exploiting the dual EPT formulation and geometric structures of the graph-based Orlicz-Sobolev space, we derive a novel regularization to propose Orlicz-Sobolev transport (OST). The resulting distance can be efficiently computed by simply solving a univariate optimization problem, unlike the high-computational two-level optimization problem for Orlicz-EPT. Additionally, we derive geometric structures for the OST and draw its relations to other transport distances. We empirically show that OST is several-order faster than Orlicz-EPT. We further illustrate preliminary evidences on the advantages of OST for document classification, and several tasks in topological data analysis.
Compositional simulation-based inference for time series
Nov 05, 2024Abstract:Amortized simulation-based inference (SBI) methods train neural networks on simulated data to perform Bayesian inference. While this approach avoids the need for tractable likelihoods, it often requires a large number of simulations and has been challenging to scale to time-series data. Scientific simulators frequently emulate real-world dynamics through thousands of single-state transitions over time. We propose an SBI framework that can exploit such Markovian simulators by locally identifying parameters consistent with individual state transitions. We then compose these local results to obtain a posterior over parameters that align with the entire time series observation. We focus on applying this approach to neural posterior score estimation but also show how it can be applied, e.g., to neural likelihood (ratio) estimation. We demonstrate that our approach is more simulation-efficient than directly estimating the global posterior on several synthetic benchmark tasks and simulators used in ecology and epidemiology. Finally, we validate scalability and simulation efficiency of our approach by applying it to a high-dimensional Kolmogorov flow simulator with around one million dimensions in the data domain.
Scaling Law of Sim2Real Transfer Learning in Expanding Computational Materials Databases for Real-World Predictions
Aug 07, 2024Abstract:To address the challenge of limited experimental materials data, extensive physical property databases are being developed based on high-throughput computational experiments, such as molecular dynamics simulations. Previous studies have shown that fine-tuning a predictor pretrained on a computational database to a real system can result in models with outstanding generalization capabilities compared to learning from scratch. This study demonstrates the scaling law of simulation-to-real (Sim2Real) transfer learning for several machine learning tasks in materials science. Case studies of three prediction tasks for polymers and inorganic materials reveal that the prediction error on real systems decreases according to a power-law as the size of the computational data increases. Observing the scaling behavior offers various insights for database development, such as determining the sample size necessary to achieve a desired performance, identifying equivalent sample sizes for physical and computational experiments, and guiding the design of data production protocols for downstream real-world tasks.
Flow matching achieves minimax optimal convergence
May 31, 2024Abstract:Flow matching (FM) has gained significant attention as a simulation-free generative model. Unlike diffusion models, which are based on stochastic differential equations, FM employs a simpler approach by solving an ordinary differential equation with an initial condition from a normal distribution, thus streamlining the sample generation process. This paper discusses the convergence properties of FM in terms of the $p$-Wasserstein distance, a measure of distributional discrepancy. We establish that FM can achieve the minmax optimal convergence rate for $1 \leq p \leq 2$, presenting the first theoretical evidence that FM can reach convergence rates comparable to those of diffusion models. Our analysis extends existing frameworks by examining a broader class of mean and variance functions for the vector fields and identifies specific conditions necessary to attain these optimal rates.
State-Separated SARSA: A Practical Sequential Decision-Making Algorithm with Recovering Rewards
Mar 18, 2024Abstract:While many multi-armed bandit algorithms assume that rewards for all arms are constant across rounds, this assumption does not hold in many real-world scenarios. This paper considers the setting of recovering bandits (Pike-Burke & Grunewalder, 2019), where the reward depends on the number of rounds elapsed since the last time an arm was pulled. We propose a new reinforcement learning (RL) algorithm tailored to this setting, named the State-Separate SARSA (SS-SARSA) algorithm, which treats rounds as states. The SS-SARSA algorithm achieves efficient learning by reducing the number of state combinations required for Q-learning/SARSA, which often suffers from combinatorial issues for large-scale RL problems. Additionally, it makes minimal assumptions about the reward structure and offers lower computational complexity. Furthermore, we prove asymptotic convergence to an optimal policy under mild assumptions. Simulation studies demonstrate the superior performance of our algorithm across various settings.
Neural-Kernel Conditional Mean Embeddings
Mar 16, 2024Abstract:Kernel conditional mean embeddings (CMEs) offer a powerful framework for representing conditional distribution, but they often face scalability and expressiveness challenges. In this work, we propose a new method that effectively combines the strengths of deep learning with CMEs in order to address these challenges. Specifically, our approach leverages the end-to-end neural network (NN) optimization framework using a kernel-based objective. This design circumvents the computationally expensive Gram matrix inversion required by current CME methods. To further enhance performance, we provide efficient strategies to optimize the remaining kernel hyperparameters. In conditional density estimation tasks, our NN-CME hybrid achieves competitive performance and often surpasses existing deep learning-based methods. Lastly, we showcase its remarkable versatility by seamlessly integrating it into reinforcement learning (RL) contexts. Building on Q-learning, our approach naturally leads to a new variant of distributional RL methods, which demonstrates consistent effectiveness across different environments.
Extended Flow Matching: a Method of Conditional Generation with Generalized Continuity Equation
Mar 03, 2024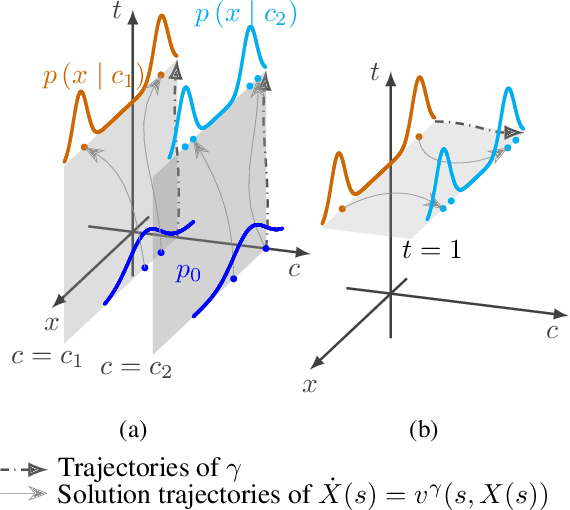
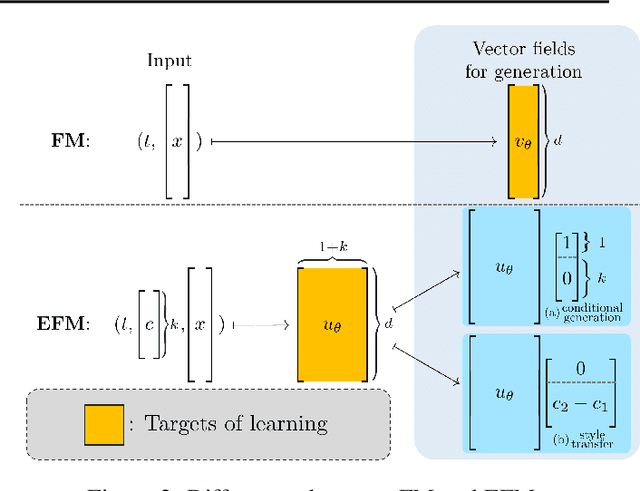
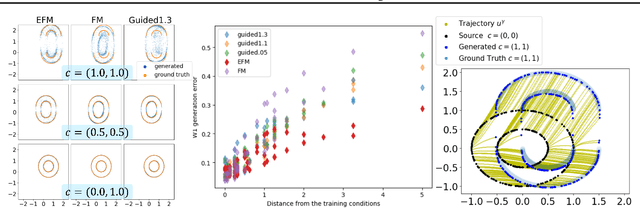
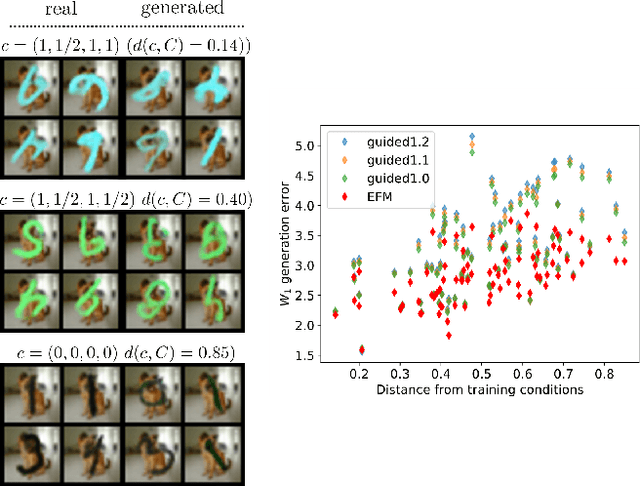
Abstract:The task of conditional generation is one of the most important applications of generative models, and numerous methods have been developed to date based on the celebrated diffusion models, with the guidance-based classifier-free method taking the lead. However, the theory of the guidance-based method not only requires the user to fine-tune the "guidance strength," but its target vector field does not necessarily correspond to the conditional distribution used in training. In this paper, we develop the theory of conditional generation based on Flow Matching, a current strong contender of diffusion methods. Motivated by the interpretation of a probability path as a distribution on path space, we establish a novel theory of flow-based generation of conditional distribution by employing the mathematical framework of generalized continuity equation instead of the continuity equation in flow matching. This theory naturally derives a method that aims to match the matrix field as opposed to the vector field. Our framework ensures the continuity of the generated conditional distribution through the existence of flow between conditional distributions. We will present our theory through experiments and mathematical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge