Generalized Sobolev Transport for Probability Measures on a Graph

We study the optimal transport (OT) problem for measures supported on a graph metric space. Recently, Le et al. (2022) leverage the graph structure and propose a variant of OT, namely Sobolev transport (ST), which yields a closed-form expression for a fast computation. However, ST is essentially coupled with the $L^p$ geometric structure within its definition which makes it nontrivial to utilize ST for other prior structures. In contrast, the classic OT has the flexibility to adapt to various geometric structures by modifying the underlying cost function. An important instance is the Orlicz-Wasserstein (OW) which moves beyond the $L^p$ structure by leveraging the \emph{Orlicz geometric structure}. Comparing to the usage of standard $p$-order Wasserstein, OW remarkably helps to advance certain machine learning approaches. Nevertheless, OW brings up a new challenge on its computation due to its two-level optimization formulation. In this work, we leverage a specific class of convex functions for Orlicz structure to propose the generalized Sobolev transport (GST). GST encompasses the ST as its special case, and can be utilized for prior structures beyond the $L^p$ geometry. In connection with the OW, we show that one only needs to simply solve a univariate optimization problem to compute the GST, unlike the complex two-level optimization problem in OW. We empirically illustrate that GST is several-order faster than the OW. Moreover, we provide preliminary evidences on the advantages of GST for document classification and for several tasks in topological data analysis.

Optimal Transport for Measures with Noisy Tree Metric

We study optimal transport (OT) problem for probability measures supported on a tree metric space. It is known that such OT problem (i.e., tree-Wasserstein (TW)) admits a closed-form expression, but depends fundamentally on the underlying tree structure over supports of input measures. In practice, the given tree structure may be, however, perturbed due to noisy or adversarial measurements. In order to mitigate this issue, we follow the max-min robust OT approach which considers the maximal possible distances between two input measures over an uncertainty set of tree metrics. In general, this approach is hard to compute, even for measures supported in $1$-dimensional space, due to its non-convexity and non-smoothness which hinders its practical applications, especially for large-scale settings. In this work, we propose \emph{novel uncertainty sets of tree metrics} from the lens of edge deletion/addition which covers a diversity of tree structures in an elegant framework. Consequently, by building upon the proposed uncertainty sets, and leveraging the tree structure over supports, we show that the max-min robust OT also admits a closed-form expression for a fast computation as its counterpart standard OT (i.e., TW). Furthermore, we demonstrate that the max-min robust OT satisfies the metric property and is negative definite. We then exploit its negative definiteness to propose \emph{positive definite kernels} and test them in several simulations on various real-world datasets on document classification and topological data analysis for measures with noisy tree metric.

Scalable Unbalanced Sobolev Transport for Measures on a Graph

Optimal transport (OT) is a popular and powerful tool for comparing probability measures. However, OT suffers a few drawbacks: (i) input measures required to have the same mass, (ii) a high computational complexity, and (iii) indefiniteness which limits its applications on kernel-dependent algorithmic approaches. To tackle issues (ii)--(iii), Le et al. (2022) recently proposed Sobolev transport for measures on a graph having the same total mass by leveraging the graph structure over supports. In this work, we consider measures that may have different total mass and are supported on a graph metric space. To alleviate the disadvantages (i)--(iii) of OT, we propose a novel and scalable approach to extend Sobolev transport for this unbalanced setting where measures may have different total mass. We show that the proposed unbalanced Sobolev transport (UST) admits a closed-form formula for fast computation, and it is also negative definite. Additionally, we derive geometric structures for the UST and establish relations between our UST and other transport distances. We further exploit the negative definiteness to design positive definite kernels and evaluate them on various simulations to illustrate their fast computation and comparable performances against other transport baselines for unbalanced measures on a graph.

Dynamic Flows on Curved Space Generated by Labeled Data

The scarcity of labeled data is a long-standing challenge for many machine learning tasks. We propose our gradient flow method to leverage the existing dataset (i.e., source) to generate new samples that are close to the dataset of interest (i.e., target). We lift both datasets to the space of probability distributions on the feature-Gaussian manifold, and then develop a gradient flow method that minimizes the maximum mean discrepancy loss. To perform the gradient flow of distributions on the curved feature-Gaussian space, we unravel the Riemannian structure of the space and compute explicitly the Riemannian gradient of the loss function induced by the optimal transport metric. For practical applications, we also propose a discretized flow, and provide conditional results guaranteeing the global convergence of the flow to the optimum. We illustrate the results of our proposed gradient flow method on several real-world datasets and show our method can improve the accuracy of classification models in transfer learning settings.

Sobolev Transport: A Scalable Metric for Probability Measures with Graph Metrics

Optimal transport (OT) is a popular measure to compare probability distributions. However, OT suffers a few drawbacks such as (i) a high complexity for computation, (ii) indefiniteness which limits its applicability to kernel machines. In this work, we consider probability measures supported on a graph metric space and propose a novel Sobolev transport metric. We show that the Sobolev transport metric yields a closed-form formula for fast computation and it is negative definite. We show that the space of probability measures endowed with this transport distance is isometric to a bounded convex set in a Euclidean space with a weighted $\ell_p$ distance. We further exploit the negative definiteness of the Sobolev transport to design positive-definite kernels, and evaluate their performances against other baselines in document classification with word embeddings and in topological data analysis.

Adversarial Regression with Doubly Non-negative Weighting Matrices

Many machine learning tasks that involve predicting an output response can be solved by training a weighted regression model. Unfortunately, the predictive power of this type of models may severely deteriorate under low sample sizes or under covariate perturbations. Reweighting the training samples has aroused as an effective mitigation strategy to these problems. In this paper, we propose a novel and coherent scheme for kernel-reweighted regression by reparametrizing the sample weights using a doubly non-negative matrix. When the weighting matrix is confined in an uncertainty set using either the log-determinant divergence or the Bures-Wasserstein distance, we show that the adversarially reweighted estimate can be solved efficiently using first-order methods. Numerical experiments show that our reweighting strategy delivers promising results on numerous datasets.

Entropy Partial Transport with Tree Metrics: Theory and Practice

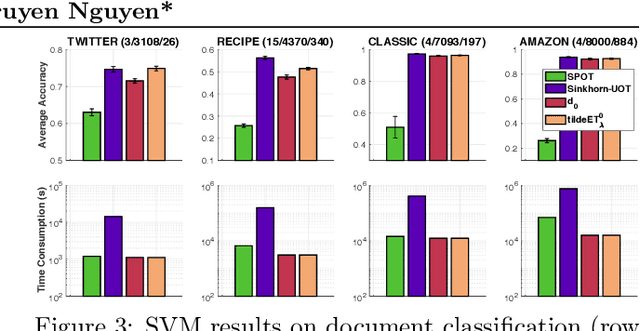
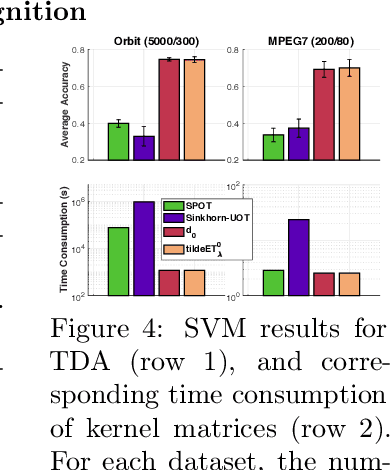
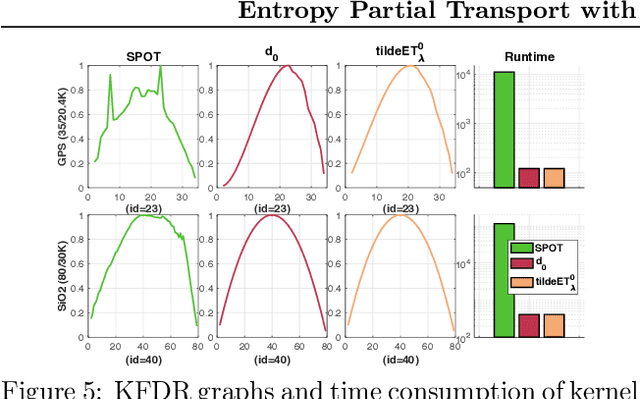
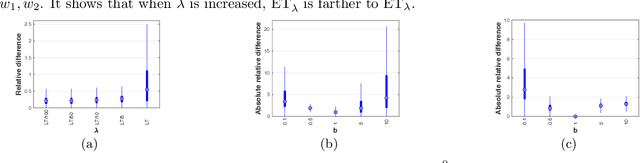
Optimal transport (OT) theory provides powerful tools to compare probability measures. However, OT is limited to nonnegative measures having the same mass, and suffers serious drawbacks about its computation and statistics. This leads to several proposals of regularized variants of OT in the recent literature. In this work, we consider an \textit{entropy partial transport} (EPT) problem for nonnegative measures on a tree having different masses. The EPT is shown to be equivalent to a standard complete OT problem on a one-node extended tree. We derive its dual formulation, then leverage this to propose a novel regularization for EPT which admits fast computation and negative definiteness. To our knowledge, the proposed regularized EPT is the first approach that yields a \textit{closed-form} solution among available variants of unbalanced OT. For practical applications without priori knowledge about the tree structure for measures, we propose tree-sliced variants of the regularized EPT, computed by averaging the regularized EPT between these measures using random tree metrics, built adaptively from support data points. Exploiting the negative definiteness of our regularized EPT, we introduce a positive definite kernel, and evaluate it against other baselines on benchmark tasks such as document classification with word embedding and topological data analysis. In addition, we empirically demonstrate that our regularization also provides effective approximations.

On the Convergence of Gradient Descent in GANs: MMD GAN As a Gradient Flow

We consider the maximum mean discrepancy ($\mathrm{MMD}$) GAN problem and propose a parametric kernelized gradient flow that mimics the min-max game in gradient regularized $\mathrm{MMD}$ GAN. We show that this flow provides a descent direction minimizing the $\mathrm{MMD}$ on a statistical manifold of probability distributions. We then derive an explicit condition which ensures that gradient descent on the parameter space of the generator in gradient regularized $\mathrm{MMD}$ GAN is globally convergent to the target distribution. Under this condition, we give non asymptotic convergence results of gradient descent in MMD GAN. Another contribution of this paper is the introduction of a dynamic formulation of a regularization of $\mathrm{MMD}$ and demonstrating that the parametric kernelized descent for $\mathrm{MMD}$ is the gradient flow of this functional with respect to the new Riemannian structure. Our obtained theoretical result allows ones to treat gradient flows for quite general functionals and thus has potential applications to other types of variational inferences on a statistical manifold beyond GANs. Finally, numerical experiments suggest that our parametric kernelized gradient flow stabilizes GAN training and guarantees convergence.