Accelerated Sampling of Rare Events using a Neural Network Bias Potential

In the field of computational physics and material science, the efficient sampling of rare events occurring at atomic scale is crucial. It aids in understanding mechanisms behind a wide range of important phenomena, including protein folding, conformal changes, chemical reactions and materials diffusion and deformation. Traditional simulation methods, such as Molecular Dynamics and Monte Carlo, often prove inefficient in capturing the timescale of these rare events by brute force. In this paper, we introduce a practical approach by combining the idea of importance sampling with deep neural networks (DNNs) that enhance the sampling of these rare events. In particular, we approximate the variance-free bias potential function with DNNs which is trained to maximize the probability of rare event transition under the importance potential function. This method is easily scalable to high-dimensional problems and provides robust statistical guarantees on the accuracy of the estimated probability of rare event transition. Furthermore, our algorithm can actively generate and learn from any successful samples, which is a novel improvement over existing methods. Using a 2D system as a test bed, we provide comparisons between results obtained from different training strategies, traditional Monte Carlo sampling and numerically solved optimal bias potential function under different temperatures. Our numerical results demonstrate the efficacy of the DNN-based importance sampling of rare events.

Dynamic Flows on Curved Space Generated by Labeled Data

The scarcity of labeled data is a long-standing challenge for many machine learning tasks. We propose our gradient flow method to leverage the existing dataset (i.e., source) to generate new samples that are close to the dataset of interest (i.e., target). We lift both datasets to the space of probability distributions on the feature-Gaussian manifold, and then develop a gradient flow method that minimizes the maximum mean discrepancy loss. To perform the gradient flow of distributions on the curved feature-Gaussian space, we unravel the Riemannian structure of the space and compute explicitly the Riemannian gradient of the loss function induced by the optimal transport metric. For practical applications, we also propose a discretized flow, and provide conditional results guaranteeing the global convergence of the flow to the optimum. We illustrate the results of our proposed gradient flow method on several real-world datasets and show our method can improve the accuracy of classification models in transfer learning settings.

Human Imperceptible Attacks and Applications to Improve Fairness

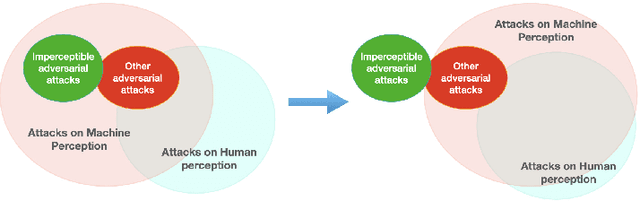
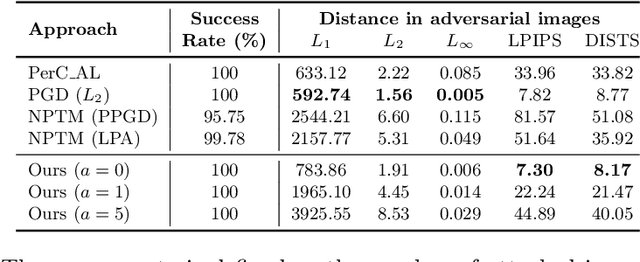
Modern neural networks are able to perform at least as well as humans in numerous tasks involving object classification and image generation. However, small perturbations which are imperceptible to humans may significantly degrade the performance of well-trained deep neural networks. We provide a Distributionally Robust Optimization (DRO) framework which integrates human-based image quality assessment methods to design optimal attacks that are imperceptible to humans but significantly damaging to deep neural networks. Through extensive experiments, we show that our attack algorithm generates better-quality (less perceptible to humans) attacks than other state-of-the-art human imperceptible attack methods. Moreover, we demonstrate that DRO training using our optimally designed human imperceptible attacks can improve group fairness in image classification. Towards the end, we provide an algorithmic implementation to speed up DRO training significantly, which could be of independent interest.

Improved Search Strategies for Determining Facial Expression

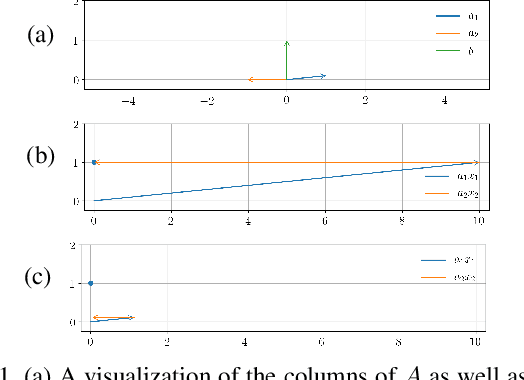
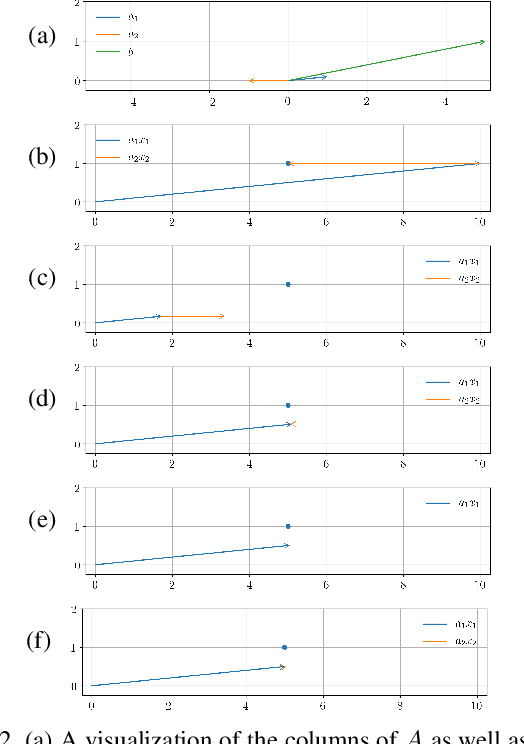
It is well known that popular optimization techniques can lead to overfitting or even a lack of convergence altogether; thus, practitioners often utilize ad hoc regularization terms added to the energy functional. When carefully crafted, these regularizations can produce compelling results. However, regularization changes both the energy landscape and the solution to the optimization problem, which can result in underfitting. Surprisingly, many practitioners both add regularization and claim that their model lacks the expressivity to fit the data. Motivated by a geometric interpretation of the linearized search space, we propose an approach that ameliorates overfitting without the need for regularization terms that restrict the expressiveness of the underlying model. We illustrate the efficacy of our approach on minimization problems related to three-dimensional facial expression estimation where overfitting clouds semantic understanding and regularization may lead to underfitting that misses or misinterprets subtle expressions.