Sobolev--Ricci Curvature

Ricci curvature is a fundamental concept in differential geometry for encoding local geometric structure, and its graph-based analogues have recently gained prominence as practical tools for reweighting, pruning, and reshaping network geometry. We propose Sobolev-Ricci Curvature (SRC), a graph Ricci curvature canonically induced by Sobolev transport geometry, which admits efficient evaluation via a tree-metric Sobolev structure on neighborhood measures. We establish two consistency behaviors that anchor SRC to classical transport curvature: (i) on trees endowed with the length measure, SRC recovers Ollivier-Ricci curvature (ORC) in the canonical W1 setting, and (ii) SRC vanishes in the Dirac limit, matching the flat case of measure-theoretic Ricci curvature. We demonstrate SRC as a reusable curvature primitive in two representative pipelines. We define Sobolev-Ricci Flow by replacing ORC with SRC in a Ricci-flow-style reweighting rule, and we use SRC for curvature-guided edge pruning aimed at preserving manifold structure. Overall, SRC provides a transport-based foundation for scalable curvature-driven graph transformation and manifold-oriented pruning.

Unregularized limit of stochastic gradient method for Wasserstein distributionally robust optimization

Distributionally robust optimization offers a compelling framework for model fitting in machine learning, as it systematically accounts for data uncertainty. Focusing on Wasserstein distributionally robust optimization, we investigate the regularized problem where entropic smoothing yields a sampling-based approximation of the original objective. We establish the convergence of the approximate gradient over a compact set, leading to the concentration of the regularized problem critical points onto the original problem critical set as regularization diminishes and the number of approximation samples increases. Finally, we deduce convergence guarantees for a projected stochastic gradient method. Our analysis covers a general machine learning situation with an unbounded sample space and mixed continuous-discrete data.

Tree-Sliced Wasserstein Distance with Nonlinear Projection

Tree-Sliced methods have recently emerged as an alternative to the traditional Sliced Wasserstein (SW) distance, replacing one-dimensional lines with tree-based metric spaces and incorporating a splitting mechanism for projecting measures. This approach enhances the ability to capture the topological structures of integration domains in Sliced Optimal Transport while maintaining low computational costs. Building on this foundation, we propose a novel nonlinear projectional framework for the Tree-Sliced Wasserstein (TSW) distance, substituting the linear projections in earlier versions with general projections, while ensuring the injectivity of the associated Radon Transform and preserving the well-definedness of the resulting metric. By designing appropriate projections, we construct efficient metrics for measures on both Euclidean spaces and spheres. Finally, we validate our proposed metric through extensive numerical experiments for Euclidean and spherical datasets. Applications include gradient flows, self-supervised learning, and generative models, where our methods demonstrate significant improvements over recent SW and TSW variants.

Distance-Based Tree-Sliced Wasserstein Distance

To overcome computational challenges of Optimal Transport (OT), several variants of Sliced Wasserstein (SW) has been developed in the literature. These approaches exploit the closed-form expression of the univariate OT by projecting measures onto (one-dimensional) lines. However, projecting measures onto low-dimensional spaces can lead to a loss of topological information. Tree-Sliced Wasserstein distance on Systems of Lines (TSW-SL) has emerged as a promising alternative that replaces these lines with a more advanced structure called tree systems. The tree structures enhance the ability to capture topological information of the metric while preserving computational efficiency. However, at the core of TSW-SL, the splitting maps, which serve as the mechanism for pushing forward measures onto tree systems, focus solely on the position of the measure supports while disregarding the projecting domains. Moreover, the specific splitting map used in TSW-SL leads to a metric that is not invariant under Euclidean transformations, a typically expected property for OT on Euclidean space. In this work, we propose a novel class of splitting maps that generalizes the existing one studied in TSW-SL enabling the use of all positional information from input measures, resulting in a novel Distance-based Tree-Sliced Wasserstein (Db-TSW) distance. In addition, we introduce a simple tree sampling process better suited for Db-TSW, leading to an efficient GPU-friendly implementation for tree systems, similar to the original SW. We also provide a comprehensive theoretical analysis of proposed class of splitting maps to verify the injectivity of the corresponding Radon Transform, and demonstrate that Db-TSW is an Euclidean invariant metric. We empirically show that Db-TSW significantly improves accuracy compared to recent SW variants while maintaining low computational cost via a wide range of experiments.

Spherical Tree-Sliced Wasserstein Distance

Sliced Optimal Transport (OT) simplifies the OT problem in high-dimensional spaces by projecting supports of input measures onto one-dimensional lines and then exploiting the closed-form expression of the univariate OT to reduce the computational burden of OT. Recently, the Tree-Sliced method has been introduced to replace these lines with more intricate structures, known as tree systems. This approach enhances the ability to capture topological information of integration domains in Sliced OT while maintaining low computational cost. Inspired by this approach, in this paper, we present an adaptation of tree systems on OT problems for measures supported on a sphere. As a counterpart to the Radon transform variant on tree systems, we propose a novel spherical Radon transform with a new integration domain called spherical trees. By leveraging this transform and exploiting the spherical tree structures, we derive closed-form expressions for OT problems on the sphere. Consequently, we obtain an efficient metric for measures on the sphere, named Spherical Tree-Sliced Wasserstein (STSW) distance. We provide an extensive theoretical analysis to demonstrate the topology of spherical trees and the well-definedness and injectivity of our Radon transform variant, which leads to an orthogonally invariant distance between spherical measures. Finally, we conduct a wide range of numerical experiments, including gradient flows and self-supervised learning, to assess the performance of our proposed metric, comparing it to recent benchmarks.

Orlicz-Sobolev Transport for Unbalanced Measures on a Graph

Moving beyond $L^p$ geometric structure, Orlicz-Wasserstein (OW) leverages a specific class of convex functions for Orlicz geometric structure. While OW remarkably helps to advance certain machine learning approaches, it has a high computational complexity due to its two-level optimization formula. Recently, Le et al. (2024) exploits graph structure to propose generalized Sobolev transport (GST), i.e., a scalable variant for OW. However, GST assumes that input measures have the same mass. Unlike optimal transport (OT), it is nontrivial to incorporate a mass constraint to extend GST for measures on a graph, possibly having different total mass. In this work, we propose to take a step back by considering the entropy partial transport (EPT) for nonnegative measures on a graph. By leveraging Caffarelli & McCann (2010)'s observations, EPT can be reformulated as a standard complete OT between two corresponding balanced measures. Consequently, we develop a novel EPT with Orlicz geometric structure, namely Orlicz-EPT, for unbalanced measures on a graph. Especially, by exploiting the dual EPT formulation and geometric structures of the graph-based Orlicz-Sobolev space, we derive a novel regularization to propose Orlicz-Sobolev transport (OST). The resulting distance can be efficiently computed by simply solving a univariate optimization problem, unlike the high-computational two-level optimization problem for Orlicz-EPT. Additionally, we derive geometric structures for the OST and draw its relations to other transport distances. We empirically show that OST is several-order faster than Orlicz-EPT. We further illustrate preliminary evidences on the advantages of OST for document classification, and several tasks in topological data analysis.

Scalable Sobolev IPM for Probability Measures on a Graph

We investigate the Sobolev IPM problem for probability measures supported on a graph metric space. Sobolev IPM is an important instance of integral probability metrics (IPM), and is obtained by constraining a critic function within a unit ball defined by the Sobolev norm. In particular, it has been used to compare probability measures and is crucial for several theoretical works in machine learning. However, to our knowledge, there are no efficient algorithmic approaches to compute Sobolev IPM effectively, which hinders its practical applications. In this work, we establish a relation between Sobolev norm and weighted $L^p$-norm, and leverage it to propose a \emph{novel regularization} for Sobolev IPM. By exploiting the graph structure, we demonstrate that the regularized Sobolev IPM provides a \emph{closed-form} expression for fast computation. This advancement addresses long-standing computational challenges, and paves the way to apply Sobolev IPM for practical applications, even in large-scale settings. Additionally, the regularized Sobolev IPM is negative definite. Utilizing this property, we design positive-definite kernels upon the regularized Sobolev IPM, and provide preliminary evidences of their advantages on document classification and topological data analysis for measures on a graph.

Tree-Sliced Wasserstein Distance on a System of Lines

Sliced Wasserstein (SW) distance in Optimal Transport (OT) is widely used in various applications thanks to its statistical effectiveness and computational efficiency. On the other hand, Tree Wassenstein (TW) and Tree-sliced Wassenstein (TSW) are instances of OT for probability measures where its ground cost is a tree metric. TSW also has a low computational complexity, i.e. linear to the number of edges in the tree. Especially, TSW is identical to SW when the tree is a chain. While SW is prone to loss of topological information of input measures due to relying on one-dimensional projection, TSW is more flexible and has a higher degree of freedom by choosing a tree rather than a line to alleviate the curse of dimensionality in SW. However, for practical applications, popular tree metric sampling methods are heavily built upon given supports, which limits their capacity to adapt to new supports. In this paper, we propose the Tree-Sliced Wasserstein distance on a System of Lines (TSW-SL), which brings a connection between SW and TSW. Compared to SW and TSW, our TSW-SL benefits from the higher degree of freedom of TSW while being suitable to dynamic settings as SW. In TSW-SL, we use a variant of the Radon Transform to project measures onto a system of lines, resulting in measures on a space with a tree metric, then leverage TW to efficiently compute distances between them. We empirically verify the advantages of TSW-SL over the traditional SW by conducting a variety of experiments on gradient flows, image style transfer, and generative models.

SAVA: Scalable Learning-Agnostic Data Valuation

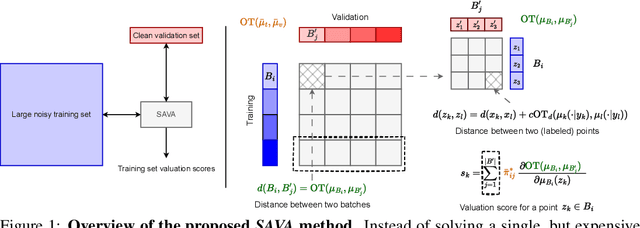
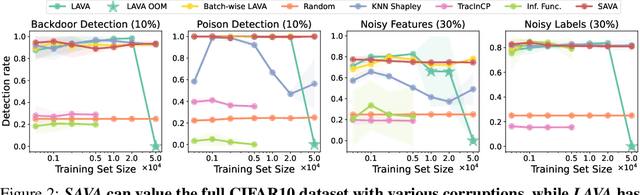
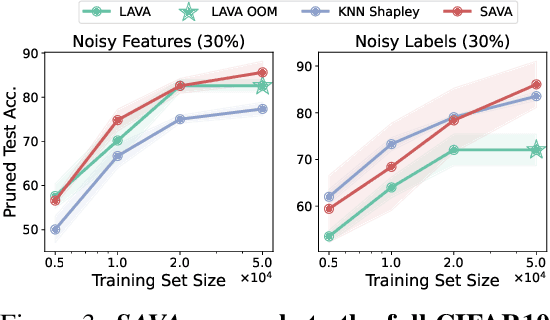
Selecting suitable data for training machine learning models is crucial since large, web-scraped, real datasets contain noisy artifacts that affect the quality and relevance of individual data points. These artifacts will impact the performance and generalization of the model. We formulate this problem as a data valuation task, assigning a value to data points in the training set according to how similar or dissimilar they are to a clean and curated validation set. Recently, LAVA (Just et al. 2023) successfully demonstrated the use of optimal transport (OT) between a large noisy training dataset and a clean validation set, to value training data efficiently, without the dependency on model performance. However, the LAVA algorithm requires the whole dataset as an input, this limits its application to large datasets. Inspired by the scalability of stochastic (gradient) approaches which carry out computations on batches of data points instead of the entire dataset, we analogously propose SAVA, a scalable variant of LAVA with its computation on batches of data points. Intuitively, SAVA follows the same scheme as LAVA which leverages the hierarchically defined OT for data valuation. However, while LAVA processes the whole dataset, SAVA divides the dataset into batches of data points, and carries out the OT problem computation on those batches. We perform extensive experiments, to demonstrate that SAVA can scale to large datasets with millions of data points and doesn't trade off data valuation performance.

Inexact subgradient methods for semialgebraic functions

Motivated by the widespread use of approximate derivatives in machine learning and optimization, we study inexact subgradient methods with non-vanishing additive errors and step sizes. In the nonconvex semialgebraic setting, under boundedness assumptions, we prove that the method provides points that eventually fluctuate close to the critical set at a distance proportional to $\epsilon^\rho$ where $\epsilon$ is the error in subgradient evaluation and $\rho$ relates to the geometry of the problem. In the convex setting, we provide complexity results for the averaged values. We also obtain byproducts of independent interest, such as descent-like lemmas for nonsmooth nonconvex problems and some results on the limit of affine interpolants of differential inclusions.