Spherical Tree-Sliced Wasserstein Distance

Sliced Optimal Transport (OT) simplifies the OT problem in high-dimensional spaces by projecting supports of input measures onto one-dimensional lines and then exploiting the closed-form expression of the univariate OT to reduce the computational burden of OT. Recently, the Tree-Sliced method has been introduced to replace these lines with more intricate structures, known as tree systems. This approach enhances the ability to capture topological information of integration domains in Sliced OT while maintaining low computational cost. Inspired by this approach, in this paper, we present an adaptation of tree systems on OT problems for measures supported on a sphere. As a counterpart to the Radon transform variant on tree systems, we propose a novel spherical Radon transform with a new integration domain called spherical trees. By leveraging this transform and exploiting the spherical tree structures, we derive closed-form expressions for OT problems on the sphere. Consequently, we obtain an efficient metric for measures on the sphere, named Spherical Tree-Sliced Wasserstein (STSW) distance. We provide an extensive theoretical analysis to demonstrate the topology of spherical trees and the well-definedness and injectivity of our Radon transform variant, which leads to an orthogonally invariant distance between spherical measures. Finally, we conduct a wide range of numerical experiments, including gradient flows and self-supervised learning, to assess the performance of our proposed metric, comparing it to recent benchmarks.

Distance-Based Tree-Sliced Wasserstein Distance

To overcome computational challenges of Optimal Transport (OT), several variants of Sliced Wasserstein (SW) has been developed in the literature. These approaches exploit the closed-form expression of the univariate OT by projecting measures onto (one-dimensional) lines. However, projecting measures onto low-dimensional spaces can lead to a loss of topological information. Tree-Sliced Wasserstein distance on Systems of Lines (TSW-SL) has emerged as a promising alternative that replaces these lines with a more advanced structure called tree systems. The tree structures enhance the ability to capture topological information of the metric while preserving computational efficiency. However, at the core of TSW-SL, the splitting maps, which serve as the mechanism for pushing forward measures onto tree systems, focus solely on the position of the measure supports while disregarding the projecting domains. Moreover, the specific splitting map used in TSW-SL leads to a metric that is not invariant under Euclidean transformations, a typically expected property for OT on Euclidean space. In this work, we propose a novel class of splitting maps that generalizes the existing one studied in TSW-SL enabling the use of all positional information from input measures, resulting in a novel Distance-based Tree-Sliced Wasserstein (Db-TSW) distance. In addition, we introduce a simple tree sampling process better suited for Db-TSW, leading to an efficient GPU-friendly implementation for tree systems, similar to the original SW. We also provide a comprehensive theoretical analysis of proposed class of splitting maps to verify the injectivity of the corresponding Radon Transform, and demonstrate that Db-TSW is an Euclidean invariant metric. We empirically show that Db-TSW significantly improves accuracy compared to recent SW variants while maintaining low computational cost via a wide range of experiments.

Monomial Matrix Group Equivariant Neural Functional Networks

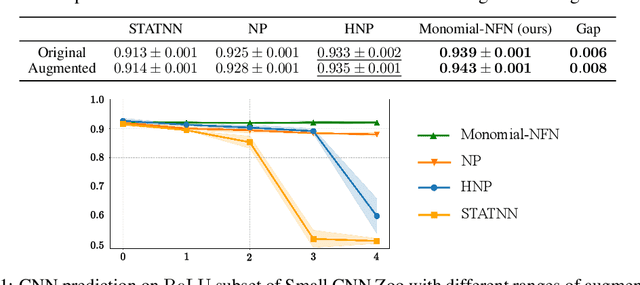
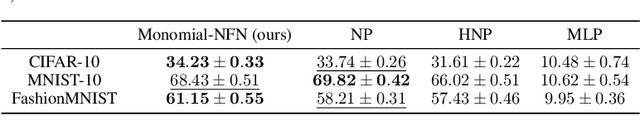
Neural functional networks (NFNs) have recently gained significant attention due to their diverse applications, ranging from predicting network generalization and network editing to classifying implicit neural representation. Previous NFN designs often depend on permutation symmetries in neural networks' weights, which traditionally arise from the unordered arrangement of neurons in hidden layers. However, these designs do not take into account the weight scaling symmetries of $\operatorname{ReLU}$ networks, and the weight sign flipping symmetries of $\operatorname{sin}$ or $\operatorname{tanh}$ networks. In this paper, we extend the study of the group action on the network weights from the group of permutation matrices to the group of monomial matrices by incorporating scaling/sign-flipping symmetries. Particularly, we encode these scaling/sign-flipping symmetries by designing our corresponding equivariant and invariant layers. We name our new family of NFNs the Monomial Matrix Group Equivariant Neural Functional Networks (Monomial-NFN). Because of the expansion of the symmetries, Monomial-NFN has much fewer independent trainable parameters compared to the baseline NFNs in the literature, thus enhancing the model's efficiency. Moreover, for fully connected and convolutional neural networks, we theoretically prove that all groups that leave these networks invariant while acting on their weight spaces are some subgroups of the monomial matrix group. We provide empirical evidences to demonstrate the advantages of our model over existing baselines, achieving competitive performance and efficiency.