A Clifford Algebraic Approach to E(n)-Equivariant High-order Graph Neural Networks

Designing neural network architectures that can handle data symmetry is crucial. This is especially important for geometric graphs whose properties are equivariance under Euclidean transformations. Current equivariant graph neural networks (EGNNs), particularly those using message passing, have a limitation in expressive power. Recent high-order graph neural networks can overcome this limitation, yet they lack equivariance properties, representing a notable drawback in certain applications in chemistry and physical sciences. In this paper, we introduce the Clifford Group Equivariant Graph Neural Networks (CG-EGNNs), a novel EGNN that enhances high-order message passing by integrating high-order local structures in the context of Clifford algebras. As a key benefit of using Clifford algebras, CG-EGNN can learn functions that capture equivariance from positional features. By adopting the high-order message passing mechanism, CG-EGNN gains richer information from neighbors, thus improving model performance. Furthermore, we establish the universality property of the $k$-hop message passing framework, showcasing greater expressive power of CG-EGNNs with additional $k$-hop message passing mechanism. We empirically validate that CG-EGNNs outperform previous methods on various benchmarks including n-body, CMU motion capture, and MD17, highlighting their effectiveness in geometric deep learning.

Equivariant Polynomial Functional Networks

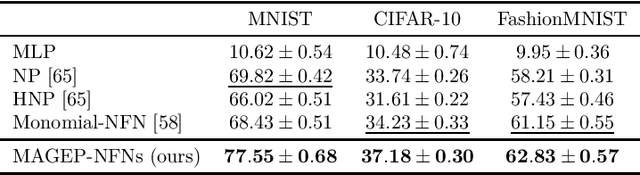
Neural Functional Networks (NFNs) have gained increasing interest due to their wide range of applications, including extracting information from implicit representations of data, editing network weights, and evaluating policies. A key design principle of NFNs is their adherence to the permutation and scaling symmetries inherent in the connectionist structure of the input neural networks. Recent NFNs have been proposed with permutation and scaling equivariance based on either graph-based message-passing mechanisms or parameter-sharing mechanisms. However, graph-based equivariant NFNs suffer from high memory consumption and long running times. On the other hand, parameter-sharing-based NFNs built upon equivariant linear layers exhibit lower memory consumption and faster running time, yet their expressivity is limited due to the large size of the symmetric group of the input neural networks. The challenge of designing a permutation and scaling equivariant NFN that maintains low memory consumption and running time while preserving expressivity remains unresolved. In this paper, we propose a novel solution with the development of MAGEP-NFN (Monomial mAtrix Group Equivariant Polynomial NFN). Our approach follows the parameter-sharing mechanism but differs from previous works by constructing a nonlinear equivariant layer represented as a polynomial in the input weights. This polynomial formulation enables us to incorporate additional relationships between weights from different input hidden layers, enhancing the model's expressivity while keeping memory consumption and running time low, thereby addressing the aforementioned challenge. We provide empirical evidence demonstrating that MAGEP-NFN achieves competitive performance and efficiency compared to existing baselines.

Equivariant Neural Functional Networks for Transformers

This paper systematically explores neural functional networks (NFN) for transformer architectures. NFN are specialized neural networks that treat the weights, gradients, or sparsity patterns of a deep neural network (DNN) as input data and have proven valuable for tasks such as learnable optimizers, implicit data representations, and weight editing. While NFN have been extensively developed for MLP and CNN, no prior work has addressed their design for transformers, despite the importance of transformers in modern deep learning. This paper aims to address this gap by providing a systematic study of NFN for transformers. We first determine the maximal symmetric group of the weights in a multi-head attention module as well as a necessary and sufficient condition under which two sets of hyperparameters of the multi-head attention module define the same function. We then define the weight space of transformer architectures and its associated group action, which leads to the design principles for NFN in transformers. Based on these, we introduce Transformer-NFN, an NFN that is equivariant under this group action. Additionally, we release a dataset of more than 125,000 Transformers model checkpoints trained on two datasets with two different tasks, providing a benchmark for evaluating Transformer-NFN and encouraging further research on transformer training and performance.

Monomial Matrix Group Equivariant Neural Functional Networks

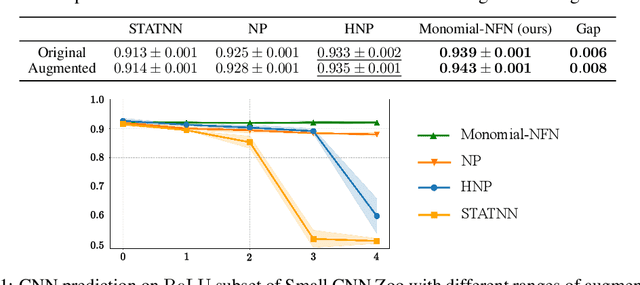
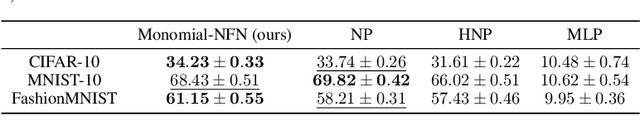
Neural functional networks (NFNs) have recently gained significant attention due to their diverse applications, ranging from predicting network generalization and network editing to classifying implicit neural representation. Previous NFN designs often depend on permutation symmetries in neural networks' weights, which traditionally arise from the unordered arrangement of neurons in hidden layers. However, these designs do not take into account the weight scaling symmetries of $\operatorname{ReLU}$ networks, and the weight sign flipping symmetries of $\operatorname{sin}$ or $\operatorname{tanh}$ networks. In this paper, we extend the study of the group action on the network weights from the group of permutation matrices to the group of monomial matrices by incorporating scaling/sign-flipping symmetries. Particularly, we encode these scaling/sign-flipping symmetries by designing our corresponding equivariant and invariant layers. We name our new family of NFNs the Monomial Matrix Group Equivariant Neural Functional Networks (Monomial-NFN). Because of the expansion of the symmetries, Monomial-NFN has much fewer independent trainable parameters compared to the baseline NFNs in the literature, thus enhancing the model's efficiency. Moreover, for fully connected and convolutional neural networks, we theoretically prove that all groups that leave these networks invariant while acting on their weight spaces are some subgroups of the monomial matrix group. We provide empirical evidences to demonstrate the advantages of our model over existing baselines, achieving competitive performance and efficiency.

E(3)-Equivariant Mesh Neural Networks

Triangular meshes are widely used to represent three-dimensional objects. As a result, many recent works have address the need for geometric deep learning on 3D mesh. However, we observe that the complexities in many of these architectures does not translate to practical performance, and simple deep models for geometric graphs are competitive in practice. Motivated by this observation, we minimally extend the update equations of E(n)-Equivariant Graph Neural Networks (EGNNs) (Satorras et al., 2021) to incorporate mesh face information, and further improve it to account for long-range interactions through hierarchy. The resulting architecture, Equivariant Mesh Neural Network (EMNN), outperforms other, more complicated equivariant methods on mesh tasks, with a fast run-time and no expensive pre-processing. Our implementation is available at https://github.com/HySonLab/EquiMesh

Design equivariant neural networks for 3D point cloud

This work seeks to improve the generalization and robustness of existing neural networks for 3D point clouds by inducing group equivariance under general group transformations. The main challenge when designing equivariant models for point clouds is how to trade-off the performance of the model and the complexity. Existing equivariant models are either too complicate to implement or very high complexity. The main aim of this study is to build a general procedure to introduce group equivariant property to SOTA models for 3D point clouds. The group equivariant models built form our procedure are simple to implement, less complexity in comparison with the existing ones, and they preserve the strengths of the original SOTA backbone. From the results of the experiments on object classification, it is shown that our methods are superior to other group equivariant models in performance and complexity. Moreover, our method also helps to improve the mIoU of semantic segmentation models. Overall, by using a combination of only-finite-rotation equivariance and augmentation, our models can outperform existing full $SO(3)$-equivariance models with much cheaper complexity and GPU memory. The proposed procedure is general and forms a fundamental approach to group equivariant neural networks. We believe that it can be easily adapted to other SOTA models in the future.