Effective Context Modeling Framework for Emotion Recognition in Conversations

Emotion Recognition in Conversations (ERC) facilitates a deeper understanding of the emotions conveyed by speakers in each utterance within a conversation. Recently, Graph Neural Networks (GNNs) have demonstrated their strengths in capturing data relationships, particularly in contextual information modeling and multimodal fusion. However, existing methods often struggle to fully capture the complex interactions between multiple modalities and conversational context, limiting their expressiveness. To overcome these limitations, we propose ConxGNN, a novel GNN-based framework designed to capture contextual information in conversations. ConxGNN features two key parallel modules: a multi-scale heterogeneous graph that captures the diverse effects of utterances on emotional changes, and a hypergraph that models the multivariate relationships among modalities and utterances. The outputs from these modules are integrated into a fusion layer, where a cross-modal attention mechanism is applied to produce a contextually enriched representation. Additionally, ConxGNN tackles the challenge of recognizing minority or semantically similar emotion classes by incorporating a re-weighting scheme into the loss functions. Experimental results on the IEMOCAP and MELD benchmark datasets demonstrate the effectiveness of our method, achieving state-of-the-art performance compared to previous baselines.

GROOT: Effective Design of Biological Sequences with Limited Experimental Data

Latent space optimization (LSO) is a powerful method for designing discrete, high-dimensional biological sequences that maximize expensive black-box functions, such as wet lab experiments. This is accomplished by learning a latent space from available data and using a surrogate model to guide optimization algorithms toward optimal outputs. However, existing methods struggle when labeled data is limited, as training the surrogate model with few labeled data points can lead to subpar outputs, offering no advantage over the training data itself. We address this challenge by introducing GROOT, a Graph-based Latent Smoothing for Biological Sequence Optimization. In particular, GROOT generates pseudo-labels for neighbors sampled around the training latent embeddings. These pseudo-labels are then refined and smoothed by Label Propagation. Additionally, we theoretically and empirically justify our approach, demonstrate GROOT's ability to extrapolate to regions beyond the training set while maintaining reliability within an upper bound of their expected distances from the training regions. We evaluate GROOT on various biological sequence design tasks, including protein optimization (GFP and AAV) and three tasks with exact oracles from Design-Bench. The results demonstrate that GROOT equalizes and surpasses existing methods without requiring access to black-box oracles or vast amounts of labeled data, highlighting its practicality and effectiveness. We release our code at https://anonymous.4open.science/r/GROOT-D554

TESGNN: Temporal Equivariant Scene Graph Neural Networks for Efficient and Robust Multi-View 3D Scene Understanding

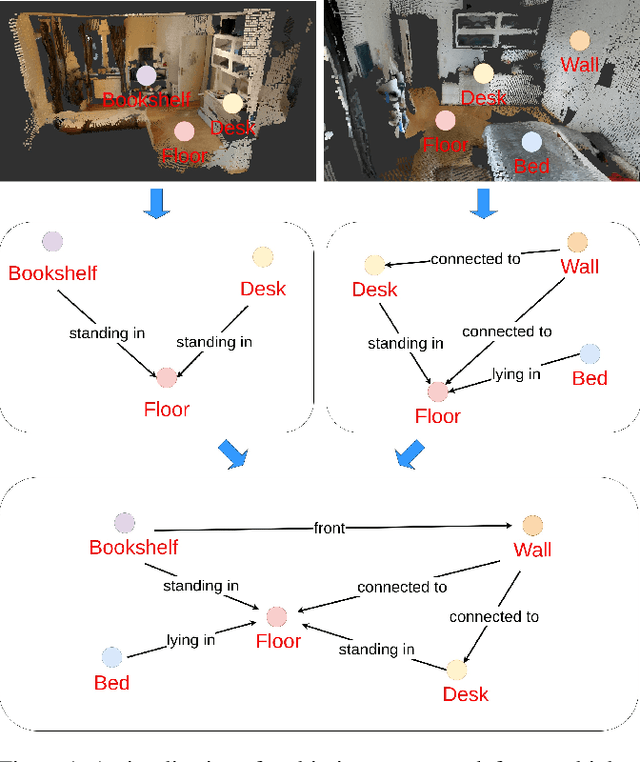
Scene graphs have proven to be highly effective for various scene understanding tasks due to their compact and explicit representation of relational information. However, current methods often overlook the critical importance of preserving symmetry when generating scene graphs from 3D point clouds, which can lead to reduced accuracy and robustness, particularly when dealing with noisy, multi-view data. This work, to the best of our knowledge, presents the first implementation of an Equivariant Scene Graph Neural Network (ESGNN) to generate semantic scene graphs from 3D point clouds, specifically for enhanced scene understanding. Furthermore, a significant limitation of prior methods is the absence of temporal modeling to capture time-dependent relationships among dynamically evolving entities within a scene. To address this gap, we introduce a novel temporal layer that leverages the symmetry-preserving properties of ESGNN to fuse scene graphs across multiple sequences into a unified global representation by an approximate graph-matching algorithm. Our combined architecture, termed the Temporal Equivariant Scene Graph Neural Network (TESGNN), not only surpasses existing state-of-the-art methods in scene estimation accuracy but also achieves faster convergence. Importantly, TESGNN is computationally efficient and straightforward to implement using existing frameworks, making it well-suited for real-time applications in robotics and computer vision. This approach paves the way for more robust and scalable solutions to complex multi-view scene understanding challenges. Our source code is publicly available at: https://github.com/HySonLab/TESGraph

Range-aware Positional Encoding via High-order Pretraining: Theory and Practice

Unsupervised pre-training on vast amounts of graph data is critical in real-world applications wherein labeled data is limited, such as molecule properties prediction or materials science. Existing approaches pre-train models for specific graph domains, neglecting the inherent connections within networks. This limits their ability to transfer knowledge to various supervised tasks. In this work, we propose a novel pre-training strategy on graphs that focuses on modeling their multi-resolution structural information, allowing us to capture global information of the whole graph while preserving local structures around its nodes. We extend the work of Wave}let Positional Encoding (WavePE) from (Ngo et al., 2023) by pretraining a High-Order Permutation-Equivariant Autoencoder (HOPE-WavePE) to reconstruct node connectivities from their multi-resolution wavelet signals. Unlike existing positional encodings, our method is designed to become sensitivity to the input graph size in downstream tasks, which efficiently capture global structure on graphs. Since our approach relies solely on the graph structure, it is also domain-agnostic and adaptable to datasets from various domains, therefore paving the wave for developing general graph structure encoders and graph foundation models. We theoretically demonstrate that there exists a parametrization of such architecture that it can predict the output adjacency up to arbitrarily low error. We also evaluate HOPE-WavePE on graph-level prediction tasks of different areas and show its superiority compared to other methods.

Sampling Foundational Transformer: A Theoretical Perspective

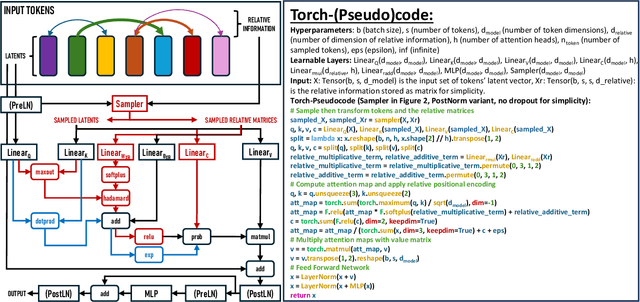
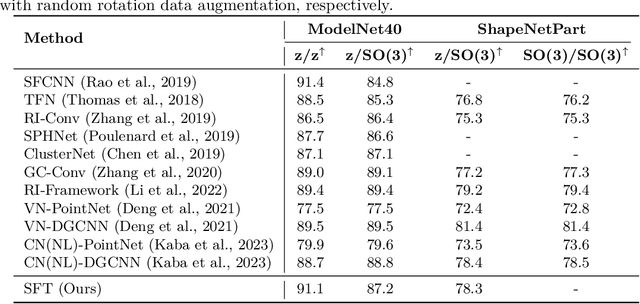
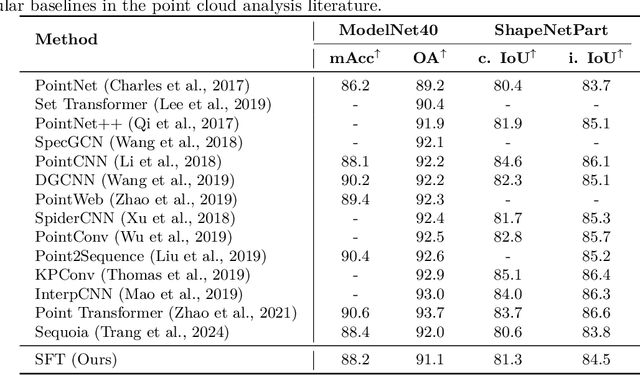
The versatility of self-attention mechanism earned transformers great success in almost all data modalities, with limitations on the quadratic complexity and difficulty of training. To apply transformers across different data modalities, practitioners have to make specific clever data-modality-dependent constructions. In this paper, we propose Sampling Foundational Transformer (SFT) that can work on multiple data modalities (e.g., point cloud, graph, and sequence) and constraints (e.g., rotational-invariant). The existence of such model is important as contemporary foundational modeling requires operability on multiple data sources. For efficiency on large number of tokens, our model relies on our context aware sampling-without-replacement mechanism for both linear asymptotic computational complexity and real inference time gain. For efficiency, we rely on our newly discovered pseudoconvex formulation of transformer layer to increase model's convergence rate. As a model working on multiple data modalities, SFT has achieved competitive results on many benchmarks, while being faster in inference, compared to other very specialized models.

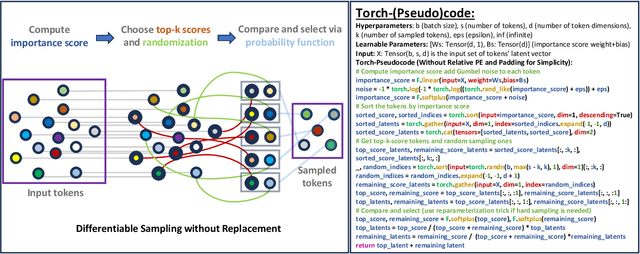
SAMSA: Efficient Transformer for Many Data Modalities

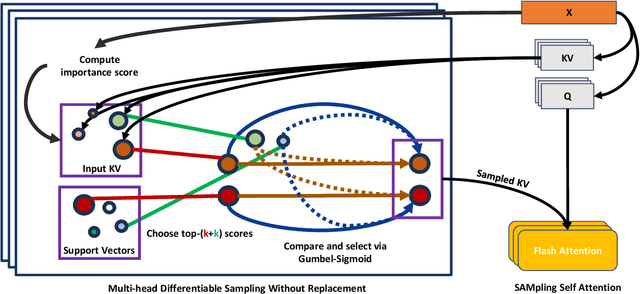
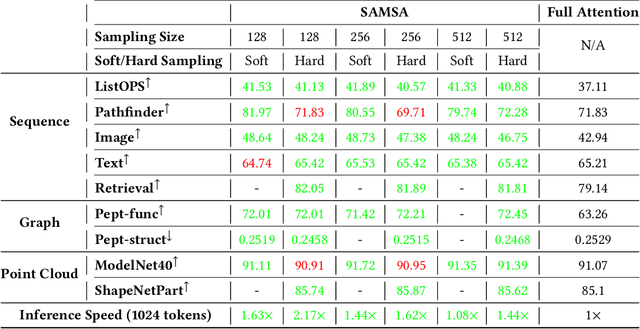
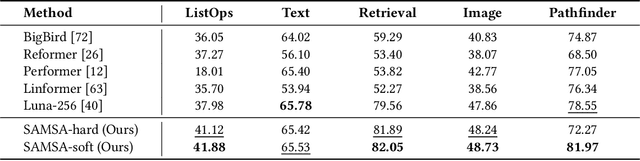
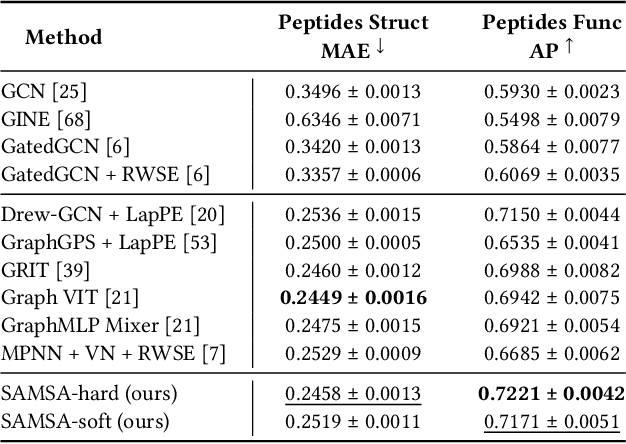
The versatility of self-attention mechanism earned transformers great success in almost all data modalities, with limitations on the quadratic complexity and difficulty of training. Efficient transformers, on the other hand, often rely on clever data-modality-dependent construction to get over the quadratic complexity of transformers. This greatly hinders their applications on different data modalities, which is one of the pillars of contemporary foundational modeling. In this paper, we lay the groundwork for efficient foundational modeling by proposing SAMSA - SAMpling-Self-Attention, a context-aware linear complexity self-attention mechanism that works well on multiple data modalities. Our mechanism is based on a differentiable sampling without replacement method we discovered. This enables the self-attention module to attend to the most important token set, where the importance is defined by data. Moreover, as differentiability is not needed in inference, the sparse formulation of our method costs little time overhead, further lowering computational costs. In short, SAMSA achieved competitive or even SOTA results on many benchmarks, while being faster in inference, compared to other very specialized models. Against full self-attention, real inference time significantly decreases while performance ranges from negligible degradation to outperformance. We release our source code in the repository: https://github.com/HySonLab/SAMSA

ESGNN: Towards Equivariant Scene Graph Neural Network for 3D Scene Understanding

Scene graphs have been proven to be useful for various scene understanding tasks due to their compact and explicit nature. However, existing approaches often neglect the importance of maintaining the symmetry-preserving property when generating scene graphs from 3D point clouds. This oversight can diminish the accuracy and robustness of the resulting scene graphs, especially when handling noisy, multi-view 3D data. This work, to the best of our knowledge, is the first to implement an Equivariant Graph Neural Network in semantic scene graph generation from 3D point clouds for scene understanding. Our proposed method, ESGNN, outperforms existing state-of-the-art approaches, demonstrating a significant improvement in scene estimation with faster convergence. ESGNN demands low computational resources and is easy to implement from available frameworks, paving the way for real-time applications such as robotics and computer vision.

Learning to Solve Multiresolution Matrix Factorization by Manifold Optimization and Evolutionary Metaheuristics

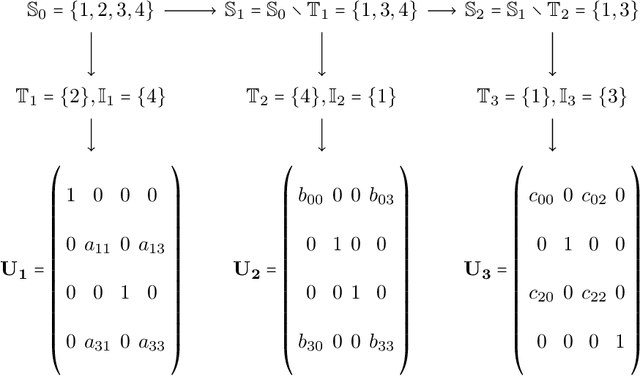
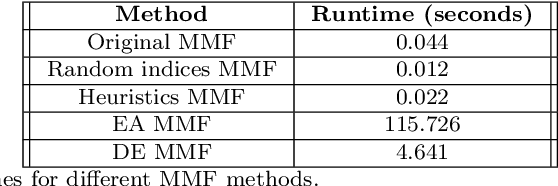
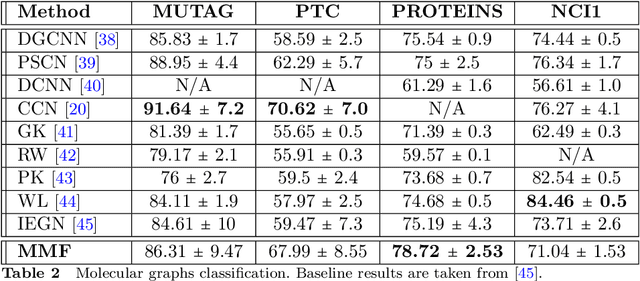
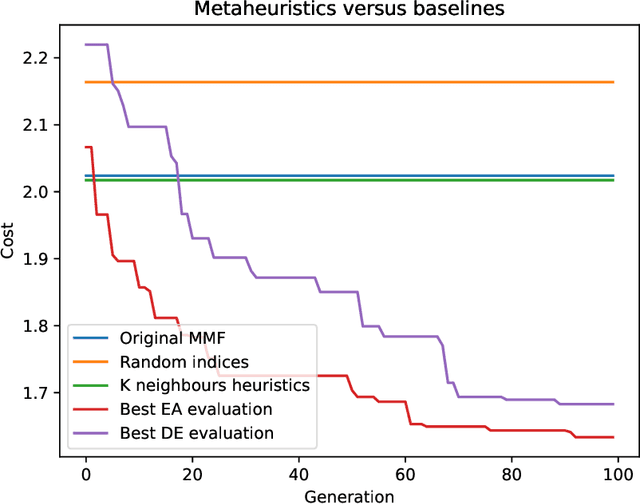
Multiresolution Matrix Factorization (MMF) is unusual amongst fast matrix factorization algorithms in that it does not make a low rank assumption. This makes MMF especially well suited to modeling certain types of graphs with complex multiscale or hierarchical strucutre. While MMF promises to yields a useful wavelet basis, finding the factorization itself is hard, and existing greedy methods tend to be brittle. In this paper, we propose a ``learnable'' version of MMF that carfully optimizes the factorization using metaheuristics, specifically evolutionary algorithms and directed evolution, along with Stiefel manifold optimization through backpropagating errors. We show that the resulting wavelet basis far outperforms prior MMF algorithms and gives comparable performance on standard learning tasks on graphs. Furthermore, we construct the wavelet neural networks (WNNs) learning graphs on the spectral domain with the wavelet basis produced by our MMF learning algorithm. Our wavelet networks are competitive against other state-of-the-art methods in molecular graphs classification and node classification on citation graphs. We release our implementation at https://github.com/HySonLab/LearnMMF

DE-HNN: An effective neural model for Circuit Netlist representation

The run-time for optimization tools used in chip design has grown with the complexity of designs to the point where it can take several days to go through one design cycle which has become a bottleneck. Designers want fast tools that can quickly give feedback on a design. Using the input and output data of the tools from past designs, one can attempt to build a machine learning model that predicts the outcome of a design in significantly shorter time than running the tool. The accuracy of such models is affected by the representation of the design data, which is usually a netlist that describes the elements of the digital circuit and how they are connected. Graph representations for the netlist together with graph neural networks have been investigated for such models. However, the characteristics of netlists pose several challenges for existing graph learning frameworks, due to the large number of nodes and the importance of long-range interactions between nodes. To address these challenges, we represent the netlist as a directed hypergraph and propose a Directional Equivariant Hypergraph Neural Network (DE-HNN) for the effective learning of (directed) hypergraphs. Theoretically, we show that our DE-HNN can universally approximate any node or hyperedge based function that satisfies certain permutation equivariant and invariant properties natural for directed hypergraphs. We compare the proposed DE-HNN with several State-of-the-art (SOTA) machine learning models for (hyper)graphs and netlists, and show that the DE-HNN significantly outperforms them in predicting the outcome of optimized place-and-route tools directly from the input netlists. Our source code and the netlists data used are publicly available at https://github.com/YusuLab/chips.git

E(3)-Equivariant Mesh Neural Networks

Triangular meshes are widely used to represent three-dimensional objects. As a result, many recent works have address the need for geometric deep learning on 3D mesh. However, we observe that the complexities in many of these architectures does not translate to practical performance, and simple deep models for geometric graphs are competitive in practice. Motivated by this observation, we minimally extend the update equations of E(n)-Equivariant Graph Neural Networks (EGNNs) (Satorras et al., 2021) to incorporate mesh face information, and further improve it to account for long-range interactions through hierarchy. The resulting architecture, Equivariant Mesh Neural Network (EMNN), outperforms other, more complicated equivariant methods on mesh tasks, with a fast run-time and no expensive pre-processing. Our implementation is available at https://github.com/HySonLab/EquiMesh