Benchmarking community drug response prediction models: datasets, models, tools, and metrics for cross-dataset generalization analysis

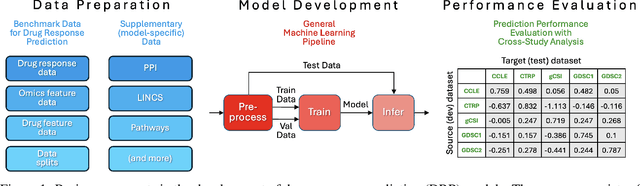
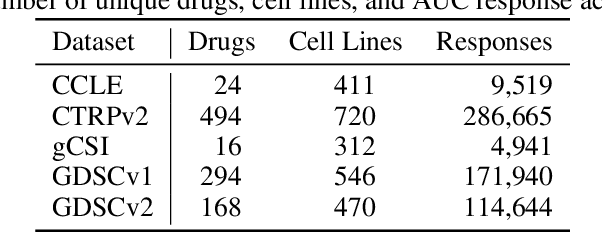
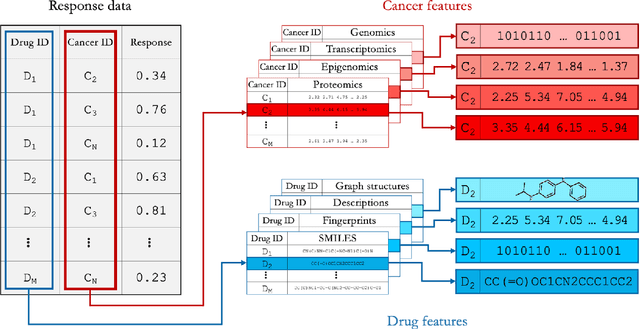
Deep learning (DL) and machine learning (ML) models have shown promise in drug response prediction (DRP), yet their ability to generalize across datasets remains an open question, raising concerns about their real-world applicability. Due to the lack of standardized benchmarking approaches, model evaluations and comparisons often rely on inconsistent datasets and evaluation criteria, making it difficult to assess true predictive capabilities. In this work, we introduce a benchmarking framework for evaluating cross-dataset prediction generalization in DRP models. Our framework incorporates five publicly available drug screening datasets, six standardized DRP models, and a scalable workflow for systematic evaluation. To assess model generalization, we introduce a set of evaluation metrics that quantify both absolute performance (e.g., predictive accuracy across datasets) and relative performance (e.g., performance drop compared to within-dataset results), enabling a more comprehensive assessment of model transferability. Our results reveal substantial performance drops when models are tested on unseen datasets, underscoring the importance of rigorous generalization assessments. While several models demonstrate relatively strong cross-dataset generalization, no single model consistently outperforms across all datasets. Furthermore, we identify CTRPv2 as the most effective source dataset for training, yielding higher generalization scores across target datasets. By sharing this standardized evaluation framework with the community, our study aims to establish a rigorous foundation for model comparison, and accelerate the development of robust DRP models for real-world applications.

DE-HNN: An effective neural model for Circuit Netlist representation

The run-time for optimization tools used in chip design has grown with the complexity of designs to the point where it can take several days to go through one design cycle which has become a bottleneck. Designers want fast tools that can quickly give feedback on a design. Using the input and output data of the tools from past designs, one can attempt to build a machine learning model that predicts the outcome of a design in significantly shorter time than running the tool. The accuracy of such models is affected by the representation of the design data, which is usually a netlist that describes the elements of the digital circuit and how they are connected. Graph representations for the netlist together with graph neural networks have been investigated for such models. However, the characteristics of netlists pose several challenges for existing graph learning frameworks, due to the large number of nodes and the importance of long-range interactions between nodes. To address these challenges, we represent the netlist as a directed hypergraph and propose a Directional Equivariant Hypergraph Neural Network (DE-HNN) for the effective learning of (directed) hypergraphs. Theoretically, we show that our DE-HNN can universally approximate any node or hyperedge based function that satisfies certain permutation equivariant and invariant properties natural for directed hypergraphs. We compare the proposed DE-HNN with several State-of-the-art (SOTA) machine learning models for (hyper)graphs and netlists, and show that the DE-HNN significantly outperforms them in predicting the outcome of optimized place-and-route tools directly from the input netlists. Our source code and the netlists data used are publicly available at https://github.com/YusuLab/chips.git

Less is More: Hop-Wise Graph Attention for Scalable and Generalizable Learning on Circuits

While graph neural networks (GNNs) have gained popularity for learning circuit representations in various electronic design automation (EDA) tasks, they face challenges in scalability when applied to large graphs and exhibit limited generalizability to new designs. These limitations make them less practical for addressing large-scale, complex circuit problems. In this work we propose HOGA, a novel attention-based model for learning circuit representations in a scalable and generalizable manner. HOGA first computes hop-wise features per node prior to model training. Subsequently, the hop-wise features are solely used to produce node representations through a gated self-attention module, which adaptively learns important features among different hops without involving the graph topology. As a result, HOGA is adaptive to various structures across different circuits and can be efficiently trained in a distributed manner. To demonstrate the efficacy of HOGA, we consider two representative EDA tasks: quality of results (QoR) prediction and functional reasoning. Our experimental results indicate that (1) HOGA reduces estimation error over conventional GNNs by 46.76% for predicting QoR after logic synthesis; (2) HOGA improves 10.0% reasoning accuracy over GNNs for identifying functional blocks on unseen gate-level netlists after complex technology mapping; (3) The training time for HOGA almost linearly decreases with an increase in computing resources.